5433

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Рассмотрим способ раскрытия неопределенностей вида

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

608.05 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Пример. Вычислить e−0,02 .

Решение. Рассмотрим функцию y = ex . Пусть x0 = 0, тогда x0 + x = −0,02, откуда x = −0,02.

y′(x0 )= (ex )′ x=0 = ex x=0 = e0 =1,

y(x0 )= ex x=0 = e0 =1.

Следовательно, e−0,02 ≈1+1 (− 0,02)=1− 0,02 = 0,98.

Ответ: e−0,02 ≈ 0,98.

Заметим, что дифференциал независимой переменной равен ее приращению, то есть dx = x, так как dy = dx = (x)′ x =1 x = x. Таким образом, дифференциал функции вычисляется по формуле:

dy = y′(x) dx.

Пример. Найти дифференциал функции y = lncos x.

Решение. y′ = (lncos x)′ =	1	(cos x)′ =	1	(− sin x)= −tgx,

	cos x		cos x
тогда dy = −tg dx.

Правило Лопиталя

при вычислении пределов от функции одного переменного, который основан на применении производных.

Пусть функции f (x) и g(x) непрерывны и дифференцируемы в

окрестности точки x0 и обращаются в нуль в этой точке: f (x0 )= g(x0 )= 0. Пусть g′(x)≠ 0 в окрестности точки x0 . Тогда, если существует предел

lim	f ′(x)	, то lim	f (x)	= lim	f ′(x)	.

x→x0 g′(x)		x→x0 g(x)		x→x0 g′(x)

Пример. Вычислить предел lim

x −1

x→1

xln x

Решение.

lim

x −1

1−1

= lim

(x −1)′

x→1

xln x

1 ln1

x→1

(xln x)′

= lim

(x)′

− (1)′

= lim

1− 0

(x)′ ln x + x (ln x)′

x→1

x→1 1 ln x + x

= lim

=1.

ln1+1

x→1

ln x +1

Пусть

функции f (x)

g(x) непрерывны и дифференцируемы в

окрестности точки x0 (кроме,

быть

может,

самой точки

x0 ), в этой

окрестности lim f (x)= lim g(x)= ∞ ,

g′(x)≠ 0. Тогда,

если существует

x→x0

предел lim

f ′(x)

, то lim

f (x)

= lim

f ′(x)

x→x0 g′(x)

x→x0 g(x)

x→x0 g′(x)

Пример. Вычислить предел lim

x2 −1

x→∞ 2x2 + 3x

Решение. lim

−1

∞2

−1

∞

= lim

(x2

−1)′

+ 3 ∞

∞

(2x2

+ 3x)′

x→∞

+ 3x 2 ∞

x→∞

′

2x − 0

∞

= lim

)

−

(1)

= lim

(2x

)

+ (3x)

4x + 3

∞

x→∞

′

x→∞

= lim

(2x)′

= lim

(4x + 3)′

x→∞

x→∞ 4

0 2

Исследование функций и построение их графиков

Одним из приложений производной является ее применение к

исследованию функций и построение их графиков.

Рекомендуемая схема исследования функции:

1.Найти область определения функции. Часто полезно учесть множество значений функции.

2.Исследовать специальные свойства функции: четность, нечетность, периодичность, свойства симметрии.

3.Исследовать поведение функции при стремлении аргумента к граничным точкам области определения и к бесконечности, то есть найти асимптоты графика функции: вертикальные и наклонные. Проанализировать расположение графика функции и его асимптот.

4.Найти интервалы монотонности функции: возрастание и убывание. Найти экстремумы функции: минимумы и максимумы.

5.Найти интервалы выпуклости функции и точки перегиба.

6.Найти точки пересечения графика с осями координат.

7.На основании результатов исследования построить эскиз графика.

Симметрия функции

Функция y = f (x)называется четной, если f (− x)= f (x). График

четной функции симметричен относительно оси Oy.

Пример. Функция y = x4 является четной, так как,

y(− x)= (− x)4 = x4 = y(x), следовательно, график этой функции

симметричен относительно оси Oy. (См. рис. 57)

					y = x4
			1
		-1	0	1	x
				Рис.57
Функция	y = f (x)	называется		нечетной,		если	f (− x)= − f (x).
График нечетной функции симметричен относительно начала координат.
Пример.	Функция	y = x3		является		нечетной,		так как
y(− x)= (− x)3	= −x3 = −y(x),		следовательно, график				этой	функции

симметричен относительно начала координат. (См. рис. 58)

		y = x3
	1
-1 0	1	x
	-1
	Рис.58

Заметим, что график четной (нечетной) функции достаточно исследовать только при x ≥ 0, а при x < 0 достроить по симметрии, то есть

симметрично относительно оси Oy (начала координат).

Функция	y = f (x) называется периодической, если существует такое
положительное число T , что		f (x + T )= f (x). Наименьшее из таких чисел
T называется	периодом	функции. График периодической функции

достаточно построить		на отрезке			оси Ox длины периода T , а затем
продолжить, сдвигая на k T , где k = ±1,± 2,… по оси Ox.
Пример. Функция y =				1	периодическая с периодом T = π , так
			sin2 x

как y(x + T )=		1	=		1	=	1		= y(x). График этой
	sin2 (x + T)			(− sin x)2			sin2
								x

функции изображен на рис. 59.

− 2π

−

3π

−π

−

3π

2π x

Рис. 59

Асимптоты графика функции

Прямую L называют асимптотой графика функции y = f (x), если

расстояние до точки M (x; y) кривой y = f (x) от прямой L стремится к

нулю при неограниченном удалении этой точки по кривой от начала координат.

Прямая	x = a является вертикальной асимптотой кривой	y = f (x),
если lim f (x)= ∞ .
x→a
Прямая	y = b является горизонтальной асимптотой кривой	y = f (x),
если lim f (x)= b.
x→∞
Прямая	y = kx + b является наклонной асимптотой кривой	y = f (x),

если существуют пределы:

k = lim f (x)

x→∞ x

и b = lim(f (x)− kx).

x→∞

Пример. Найти асимптоты кривой y = x −1.

Решение. Данная функция определена в интервалах (− ∞;1) и (1;+∞).

Так как

lim

= ∞, то прямая x =1 есть вертикальная

x −

x→1

1 1−1 0

асимптота данной кривой.

Горизонтальных

асимптот

кривая

не

имеет, так

как предел

lim

∞ = lim

(x2 )′

= lim

= ∞

не

является

конечной

x −1

(x −1)′

∞

x→∞

величиной.

Наклонные асимптоты находим в виде уравнения прямой y = kx + b:

k = lim

f (x)

= lim

∞

= lim

(x)′

= lim

=1;

(x −1)x

−1

∞

(x −1)′

x→∞

b = lim(f (x)− kx)

= lim

−

1 x

= lim

=1.

x→∞

x→∞ x −1

Таким образом, существует наклонная асимптота y = x +1.

Участки возрастания и убывания функции.

Точки минимума и максимума

Функция y = f (x)	называется	возрастающей		(убывающей) на
интервале (a;b), если для любых точек		x1,	x2 (a;b)	таких, что x1 < x2 ,
имеет место неравенство: f (x1 )< f (x2 )		(f (x1 )> f (x2 )).
Дифференцируемая	на интервале		(a;b) функция y = f (x)

возрастает (убывает) на интервале (a;b), тогда и только тогда, когда для любого x (a;b): f ′(x)> 0 (f ′(x)< 0).

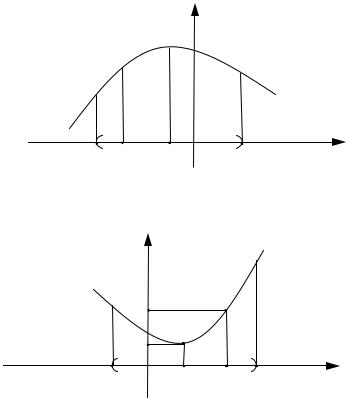
Точка x0 называется точкой максимума (минимума) функции

y= f (x), если:

1)функция y = f (x) определена в некоторой ε - окрестности точки x0 ;

2) для любого x из ε - окрестности точки x0 справедливо неравенство:

f (x)< f (x0 ) (f (x)> f (x0 )) (См. рис. 60 и 61).

f (x0 ) f (x)

x0 −ε x	x0 0	x0 +ε	x
	т. max
		Рис. 60
y
	f (x)
f(x0 )
x0 −ε 0	x0	x x0 +ε	x
	т. min
	Рис. 61
Точки максимума и минимума функции называются точками
экстремума функции.
Необходимое условие экстремума: если			x0 – точка экстремума

функции y = f (x), то в этой точке либо f ′(x0 )= 0, либо производная не существует.

Достаточные условия экстремума: пусть функция y = f (x)

дифференцируема и непрерывна в ε – окрестности критической точки x0

кроме, быть может, самой точки x0 , тогда, если ее первая производная

меняет знак минус на плюс (плюс на минус) при переходе через точку x0 , то

x0 – точка максимума (минимума) функции y = f (x).

Пример. Найти интервалы монотонности и точки экстремума функции

y =

x −1

Решение. Областью определения D данной функции

y является вся

числовая ось R, кроме точки x =1, то есть D = R \{1}.

Находим первую производную:

′

2 ′

′

y′ =

) (x −1)− x

(x −1)

(x −1)2

−1

2x (x −1)− x2 1

2x2 − 2x − x2

x2 − 2x

(x −1)2

Используя необходимые условия экстремума, находим критические

точки:

y′ = 0 x2

− 2x = 0

или

x(x − 2)= 0, откуда x = 0 или x

= 2.

y′ не существует (x −1)2 = 0, откуда x3

=1.

Используем достаточные условия экстремума. Наносим три

критические

точки

= 0;

x2 = 2;

x3 =1

на

область определения D

функции y . Они разбивают область

D на четыре интервала. Определяем

знак функции y′

в каждом интервале.

y′

–

Так как

= 0 D и при переходе через эту точку

y′ меняет знак

плюс на минус, то x1

= 0 – точка максимума функции y .

Так как	x2 = 2 D и при переходе через эту точку		y′ меняет знак
минус на плюс, то x2		= 2 – точка минимума функции y .
Так как	при	любом x (− ∞;0) или x (2;+∞)	y′ > 0, то в

интервалах (− ∞;0) и (2;+∞) функция y монотонно возрастает.

Так как при любом x (0;1) или x (1;2) y′ < 0, то в интервалах

(0;1) и (1;2) функция y монотонно убывает.

Интервалы выпуклости и вогнутости кривой.

Точки перегиба

График функции y = f (x) называется выпуклым вниз в интервале

(a;b), если он расположен ниже касательной, проведенной в любой точке x

этого интервала (См. рис. 62).

Рис. 62

График функции y = f (x) называется выпуклым вверх в интервале

(a;b), если он расположен выше касательной, проведенной в любой точке x

этого интервала (См. рис. 63).

a 0

Рис. 63

Достаточное условие выпуклости (вогнутости) графика функции:

если f ′′(x)< 0 в интервале (a;b), то график функции y = f (x)

является выпуклым вниз в этом интервале; если же f ′′(x)> 0, то в интервале

(a;b) график функции y = f (x) – выпуклый вверх.

Пусть функция y = f (x) дифференцируема в интервале (a;b) и x0 (a;b). Точку (x0 ; f (x0 )) графика функции y = f (x) называют точкой перегиба этого графика, если существует такая ε – окрестность точки x0 оси

Ox, в границах которой график функции y = f (x) слева и справа от точки x0 имеет разные направления выпуклости (См. рис. 64).

a x0 −ε 0 x0 x0+ε b	x
Рис. 64

Необходимое условие перегиба функции y = f (x) в точке x0 : если x0

– точка перегиба функции y = f (x) и функция y = f (x) имеет в некоторой

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023607.67 Кб05429.pdf
#
21.11.2023129.25 Кб0543.pdf
#
21.11.2023607.74 Кб05430.pdf
#
21.11.2023607.9 Кб05431.pdf
#
21.11.2023607.98 Кб05432.pdf
#
21.11.2023608.05 Кб05433.pdf
#
21.11.2023608.24 Кб05434.pdf
#
21.11.2023609.03 Кб05435.pdf
#
21.11.2023609.53 Кб05436.pdf
#
21.11.2023610 Кб05437.pdf
#
21.11.2023610.05 Кб05438.pdf