Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3632

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

377.79 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Задача. Найти кривую, проходящую через точку М (х; у), если угловой коэффициент касательной к ней в любой точке кривой равен квадрату ординаты точки касания.

1.16М(2, 1)

1.17М(−3, 2)

1.18М(−1, − 3)

1.19М(3, − 2)

1.20М (2, − 1)

Задача. Найти закон движения и скорость движущегося тела, если скорость его возрастает пропорционально пройденному пути, и если в начальный момент движения тело находилось в S0 м от начала отсчёта пути и имело скорость V0 м/сек.

1.21	S0 = 5 ,		V0 = 25
1.22	S0	= 3,	V0	= 18
1.23	S0	= 4 ,	V0	= 20
1.24	S0	= 8,	V0	= 24
1.25	S0	= 6 ,	V0	= 30

Задача. Исследовать закон истечения воды из полусферической чаши. За какое время t вода, заполняющая чашу диаметром D, вытечет через круглое отверстие в дне чаши диаметром d?

1.26	D = 2 м,	d = 0,2 м
1.27	D = 1м,	d = 0,1м
1.28	D = 3м,	d = 0,2 м
1.29	D = 1м,	d = 0,2 м
1.30	D = 2 м,	d = 0,1м

§3. Дифференциальные уравнения первого порядка. Типы уравнений и методы их решений.

Дифференциальное уравнение первого порядка в общем случае можно записать в виде

F (x, y, y′) = 0 .

Если y′ можно явно выразить через оставшиеся переменные, то уравнение записывается в форме Коши

y′ = f (x, y) .

Для уравнения I порядка общим решением будет функция

y = ϕ(x,C) ,

где С – произвольная постоянная.

Частным решением дифференциального уравнения I порядка

называется	любая функция	y = ϕ (x,C0 ) , полученная	из общего	решения
y = ϕ(x,C)	при конкретном	значении С = С0 . Это	конкретное	значение

С = С0 получается после подстановки в общее решение начальных условий, а именно: при x = x0 функция у должна быть равна заданному значению y0 .

3.1. Уравнения с разделяющимися переменными

Если в дифференциальном уравнении

dy = f (x, y) dx

правая часть может быть представлена в виде произведения функций

f (x, y) = f (x) × f ( y) ,

то такое уравнение называют уравнением с разделяющимися переменными.

Пример 1.	Найти общее решение уравнения (x 2 − 1) y′ − 2xy 2 = 0 .
Решение. Разрешим его относительно производной
	y¢ =	2xy 2			,
	y¢ =				,
		(x 2 -1)
Получим	уравнение с разделяющимися			переменными, т.к. правая часть
уравнения	f (x, y) =			2x		× y 2 .

			(x 2 -1)
			(x 2 -1)

Проделаем операцию разделения переменных, записывая y¢ = dy .

								dx
dy	=	2x	× y 2	или	dy	=	2x	× dx , где y ¹ 0 .
	=		× y 2	или		=	(x 2 -1)	× dx , где y ¹ 0 .
dx (x 2 -1)					y 2		(x 2 -1)

Справа и слева от знака равенства стоят дифференциалы некоторых функций, которые отличаются только постоянным слагаемым.

Интегрируя обе части

∫	dy		= ∫		2x		× dx
	y	2		(x	2	-1)

получим -	1	= ln(x 2 -1) + C - общее решение дифференциального уравнения.

	y	1

Сюда следует добавить также решение y = 0 ,			которое мы потеряли при
делении уравнения на y 2 . Такое решение			называется особым, оно

удовлетворяет дифференциальному уравнению, но не может быть получено из общего решения.

Аналогично строится общее решение и для уравнения, записанного в

дифференциальной форме

P1 (x)Q1 ( y)dx + P2 (x)Q2 ( y)dy = 0 .

Пример 2. Решить задачу Коши для дифференциального уравнения xdx + ydy = 0 при начальных условиях y(0) = 2 .

Решение. Это уравнение в дифференциальной форме. Перенесем первое слагаемое в правую часть: ydy = -xdx . Получим уравнение с разделёнными

переменными.					Интегрируя обе	части	∫ ydy = -∫ xdx ,	получим
	y 2	= -	x 2	+ C .
2		= -	2	+ C .
2			2
Тогда			x 2 + y 2		= 2C - общий	интеграл	дифференциального	уравнения.
Подставим начальные условия:						0 2 + 22 = 2C , найдем С = 2 и получим
				x 2 + y 2 = 4 - частный интеграл заданного уравнения.

Стратегия решения дифференциальных уравнений – свести их к уравнениям с разделяющимися переменными.

Задание №2

Решить задачу Коши.

2.01(х2 − 1)у′ + 2ху2 = 0

2.02х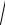1 + у2 dx + y1 + x2 dy = 0

2.03xy(1 + x2 )y′ = 1 + y 2

2.04e y (1 + x2 )y′ − 2x(1 + e y )= 0

2.052x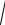1 − y 2 dx + ydy = 0

2.06sec2 x tg y dx + sec2 y tg x dy = 0

2.073e x tg y dx + (1 + e x )sec2 y dy = 0

2.08y′ = (2 y − 1)ctg x

	e1+x	2		e2 x
2.09			tg y dx −		dy = 0
				x − 1

2.10tg x dy − (1 + y)dx = 0

2.11(1 + y 2 )y′ − y = 0

2.12x2 y′ − x + 1 = 0

2.13dy − y 2 tg x dx = 0

2.14y = y′ln y

2.15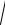6 y − y 2 dx − (4 + x2 )dy = 0

2.16x(y6 + 1)dx + y 2 (x4 + 1)dy = 0

у(0) = 1
y(			)= 0
		3
y(1) = 1
y(0) = 0
y(0) = 0
	π			=	π
y					4
	4
y(0) = π
				4
	π			= 5
y
	6
y(1) = π
				2
	π
				= 0
y
	2
	1			= 1
y

	2

y(1) = 1

у(0) = 1 y(2) = 1 y(2) = 6

у(0) = 1

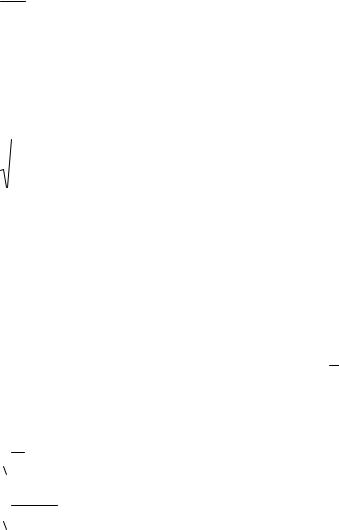
2.17	dx	+	dy	= 0
	x(y − 1)		y(x + 2)

2.18yy′ + e y = 0 x

2.19(1 + e2 x )y 2 dy = e x dx

2.20y¢ = 2x− y

2.21	1 + cos 2x	+ y′ = 0

	1 = sin 2 y

2.22yy′ = -2x sec y

2.23sin x × y′ = y cos x

2.24y¢ = (1 + y 2 )× x

2.25y′ = y × ln x

2.26y¢ = xe x− y

2.27 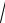y sin x dx = dy

2.28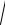1 - y 2 dx - xydy = 0

2.29	y	′	−	x	y = 0
				1 + x2

2.30	ln y x dy = ydx

y(1) = 1

y(1) = 0

y(0) = 0

у(0) = 1

π = y 0

y(0) = π

π = y 2

y(0) = 0

y(1) = 1

y(2) = 2

π = y 1

y(1) = 1

y(0) = 8

y(1) = 1

3.2. Однородные дифференциальные уравнения

Дифференциальное уравнение y′ = f (x, y) называется однородным,

если его правая часть	f (x, y) есть однородная функция, удовлетворяющая
условию f (tx,ty) = f (x, y)	для любых t, т.е. при умножении ее аргументов
на одно и то же число значение функции не изменяется.

Однородное уравнение преобразуется к уравнению с разделяющимися

переменными при помощи подстановки y = u или, что то же самое, y = u × x , x

где u = u(x) - новая неизвестная функция.

Пример 1. Решить задачу Коши для дифференциального уравнения

(x2 − y 2 )dx + 2xydy = 0 при начальных условиях y(1) = 1.

Решение. Представим уравнение в форме Коши, выразив y′

y¢ =

y 2

- x 2

2xy

Данное уравнение будет

однородным,

т.к. правая часть является

однородной функцией:

f (tx,ty) =

(ty)2

- (tx)2

t 2 ( y2

- x2 )

( y 2 - x2 )

= f (x, y) .

2tx × ty

t 2 ×

2xy

Применим подстановку

= u .

Чтобы

найти неизвестную функцию u(x) ,

подставим в уравнение функцию y = u × x и ее производную y′ = u′ × x + u .

Получим уравнение с разделяющимися переменными относительно u и x :

u¢ x + u = u 2 -1 , 2u

xu¢ = u 2 -1 - u , 2u

x du = − u 2 + 1 , dx 2u

2udu = − dx .
u 2 + 1	x

Интегрируя последнее равенство, получим общее решение преобразованного уравнения:

ln(u 2 + 1)= −ln

+ lnC

или

u 2 + 1 =

− 1

Заменяя и на

, получим

- общий интеграл данного

уравнения.

Решим задачу Коши. Подставим начальные условия в общее решение: 1 = С − 1, отсюда С = 2 , и частный интеграл будет иметь вид

y2	=	2	− 1	или	x2 + y 2 = 2x .
x2		x

Пример 2. Решить задачу Коши для дифференциального уравнения

		x		−	1

xy′ = y 1	+ ln		при начальных условиях	y(1) = e 2 .


		y

Решение. Разрешим данное уравнение относительно производной

				y′ =	y		y
						1 + ln		.
						1 + ln		.
					x		x
Правая	часть		уравнения	есть функция			отношения		y	, следовательно,
Правая	часть		уравнения	есть функция			отношения			, следовательно,
									x
уравнение		однородное.		Применим			подстановку			y = ux ,
y ′ =	u ′x	+	u

u′x + u = u(1 + ln u),

u′x = u ln u .

Разделяя переменные и интегрируя, получим

du x = u ln u , dx

u ln u

∫

d ln u

= ∫

+ ln

ln u

u = eСx ,

ln u

= ln

+ ln

ln u

= ln

Сx

, ln u = Сx ,

Возвращаясь к исходной переменной, получим

y	= eСx	или	y = xeСx - общее решение уравнения.

x

Найдём частное решение при данных начальных условиях:

e-	1	=1× eС×1 ,	С = - 1 .
	2

Таким образом

-1 x

y = xe 2 - частное решение.

Замечание. Однородное уравнение часто задаётся в дифференциальной форме:

P(x, y)dx + Q(x, y)dy = 0 ,

где функции P(x, y) и Q(x, y) - однородные функции одинакового измерения, т.е.

P(tx, ty) = t k P(x, y) ;

Q(tx,ty) = t k P(x, y) .

Задание №3

Решить задачу Коши:

3.01

xy′ − y = xtg

y(1) = π

3.02

(x2 + y 2 )dx − xydy = 0

y(1) =

3.03

y′ =

y(1) = 1

+ xy

y′ = 4 +

y 2

y(1) = 2

3.04

3.05

xy′ − y −

= 0

y(1) = 1

3.06

x cos

dy + x − y cos

dx = 0

y(1) = 0

3.07

(y − x)ydx + x2 dy = 0

y(1) = 1

3.08

(y 2 − x2 )dx + 2xydy = 0

y(1) = 0

3.09

(x + y)dx + (x + 2 y)dy = 0

y(1) = 0

3.10

y 2dx + (x2 − xy)dy = 0

y(1) = 1

y(1) =

3.11

xy′sin

+ x = y sin

3.12

(y 2 − 2xy)dx + xydy = 0

y(2) = 1

3.13

2xy + 2 y 2 = (x2 + xy)y′

y(1) = 2

(y +

)dx = xdy

y(1) = 0

3.14

x2 + y 2

3.15

y′ =

+ sin

y(1) = π

3.16

ydx + (y − x)dy = 0

y(0) = 1

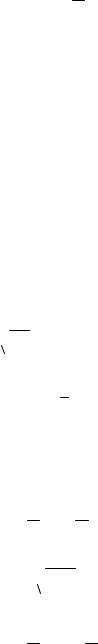
3.17xy′ = x + 2 y

3.18(x3 + y3 )dx − xy 2 dy = 0

3.19xy′ + x cos y − y + x = 0

		x
					y
3.20	xdy = y − x sec					dx

					x
3.21	xy′ = y − x sec2			y
				x

3.22	x2 y′ = xy + y 2 − x2
3.23	(x2 + y 2 )y′ = xy
3.24	xy′ = x ctg	y	+ y

		x

3.25( 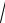xy + x)dy = ydx

−y

3.26xy′ = xe x + y

3.27y 2 dx + x(x − y)dy = 0

3.28y′ = y − tg y

3.29xy′ − 3 y 2 x − y = 0

3.30y′ = y + cos y

y(1) = 0

y(1) = π

y(1) = 0

y(1) = π

y(1) = 1

y(0) = 1

y(1) = 0

y(0) = 1

y(1) = 0

y(1) = 1

y(1) = π

y(1) = 1

y(1) = 0

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023377.47 Кб03628.pdf
#
21.11.2023377.53 Кб13629.pdf
#
21.11.2023111.98 Кб0363.pdf
#
21.11.2023377.57 Кб03630.pdf
#
21.11.2023377.72 Кб03631.pdf
#
21.11.2023377.79 Кб03632.pdf
#
21.11.2023377.82 Кб03633.pdf
#
21.11.2023378 Кб03634.pdf
#
21.11.2023378.19 Кб03635.pdf
#
21.11.2023378.43 Кб03636.pdf
#
21.11.2023378.47 Кб13637.pdf