
книги / Сопротивление материалов.-1
.pdf
которое показывает, что сумма нормальных напряжений на двух взаимно перпендикулярных площадках постоянна, откуда следует, что если с изменением угла α нормальное напряжение на одной площадке растет, то на другой – убывает.
4.3. Главные площадки. Главные напряжения
Главными называются площадки, на которых отсутствуют касательные напряжения. Положение главных площадок определяется по формуле
tg 2α0 = − |
2τx |
. |
(4.8) |
|
σx −σy |
||||
|
|
|
Нормальные напряжения, действующие на главных площадках, называются главными напряжениями. Главные напряжения являются экстремальными, т.е. одно главное напряжение имеет наибольшее, другое – наименьшее из возможных значений нормальных напряжений на множестве площадок, проходящих через исследуемую точку.
Определяются главные напряжения по формулам (4.5) и (4.6), где вместо угла α подставляется угол наклона главных площа-
док α0.
Вместо формул (4.5) и (4.6) главные напряжения могут определяться по формуле
σглI,II = |
σx + σy |
± |
1 |
|
(σx −σy )2 + 4τ2x . |
(4.9) |
|
2 |
2 |
||||||
|
|
|
|
|
Знаки в формуле (4.9) расставляются таким образом, чтобы удовлетворялись условия: если σx > σy, то σглI >σглII, и наоборот.
При изучении плоского напряженного состояния в точке обычно рассматриваются две задачи:
1. По известным напряжениям на главных площадках требуется определить нормальные и касательные напряжения на произвольных площадках. В этом случае для определения напряжений пользуются формулами (4.3), (4.5) и (4.6), в которых вместо σх и σу подставляются главные напряжения. Например, известны главные напряжения, действующие по граням элемен-
51
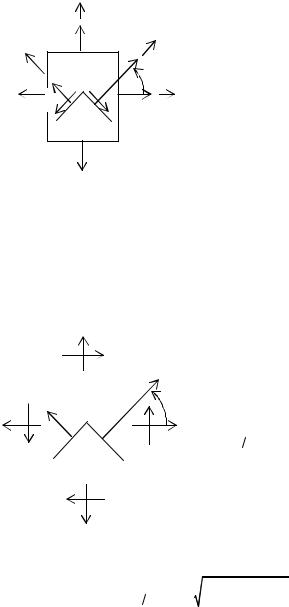
ута σ1 и σ2 (рис. 4.5). Требуется
|
|
σ2 |
х1 |
|
y1 |
|
σх1 |
|
|
|
|
|
||
|
σу1 |
α |
|
|
σ1 |
τу1 |
τх |
σ1 |
х |
|
||||
|
|
1 |
|
|
|
|
σ2 |
|
|
|
|
Рис. 4.5 |
|
|
найти нормальные и касательные напряжения на двух наклонных площадках:
σx |
= |
σ1 +σ2 |
+ |
|
σ1 −σ2 |
|
cos 2α; |
|
|||
2 |
|
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
(4.10) |
||
|
|
σ1 +σ2 |
|
|
|
σ1 − |
σ2 |
|
|||
σó |
= |
|
− |
|
cos 2α; |
|
|||||
2 |
|
2 |
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|||
|
|
τx = |
|
σ1 −σ2 |
sin 2α; |
|
|||||
|
|
|
|
|
|||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
τy = −τx . |
(4.11) |
||||||
|
|
|
|
|
1 |
1 |
|
||||
2. По известным нормальным и касательным напряжениям на произвольных взаимно перпендикулярных площадках необходимо определить главные напряжения и положение главных площадок. Задача решается с помощью формул (4.8) и (4.9). Пример задачи дан на рис. 4.6. Полагаем, что в задачах σх> σу.
σНаибольшие и наименьшие
укасательные напряжения дейст-
|
|
|
|
|
|
τу |
σmax |
|
|
вуют на площадках, располо- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
женных под углом 45° к глав- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
α0 |
|
|
ным |
площадкам. Они |
вычис- |
||
|
|
|
|
σmin |
|
|
|
|
|
|
|||||||
σх |
|
|
|
|
|
|
τх |
|
σх |
ляются по формуле |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
τ |
|
=±(σmax −σmin ). |
(4.12) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
max min |
|
2 |
|
|
|
τх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
по граням элемента |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
действуют не главные, а нор- |
||||
|
|
|
τу |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
мальные и касательные напря- |
||||||
|
|
|
|
|
σу |
|
|
|
|
жения, то экстремальные каса- |
|||||||
|
|
|
|
|
Рис. 4.6. |
|
|
|
|
тельные |
|
напряжения |
опреде- |
||||
|
|
|
|
|
|
|
|
|
ляются по формуле |
|
|||||||
|
|
|
|
|
|
τmax min =± |
1 |
|
(σx −σy )2 +4τ2x . |
(4.13) |
|||||||
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На площадках с максимальным касательным напряжением нормальные напряжения определяются по формуле
σ = |
σx +σy |
. |
(4.14) |
|
2 |
||||
|
|
|
4.4.Объемное напряженное состояние
4.4.1.Определение максимальных касательных напряжений
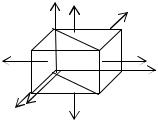
При объемном напряженном состоянии по граням элементарного параллелепипеда действуют все три главных напряже-
ния – σ1, σ2, σ3. |
вычисление |
|
|
|
|
|
|
|
Рассмотрим |
|
|
|
|
у |
σ |
|
|
максимальных касательных на- |
|
|
|
|
3 σ2 |
|||
|
|
|
|
|
|
|||
пряжений, возникающих на пло- |
|
|
|
|
|
|
|
|
щадках, параллельных действию |
|
|
|
|
|
|
|
|
главных напряжений. Так как на |
|
|
|
|
|
|
σ1 |
|
площадке, параллельной главно- |
|
σ1 |
|
х |
||||
му напряжению σ3 (рис. 4.7), |
|
|
|
|
σ2 |
|
|
|
нормальные и касательные на- |
|
|
|
|
|
|
||
пряжения целиком определяют- |
|
z |
σ3 |
|||||
|
|
|
|
|
||||
ся величинами σ1 и σ2, макси- |
|
|
|
|
|
|||
|
|
|
|
|
Рис. 4.7. |
|||
мальное касательное напряже- |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
ние согласно формуле (4.12) |
|
|
|
|
|
|
|
|
|
τ = |
σ2 – σ3 |
. |
|
(4.15) |
|||
|
|
|
|
|||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На площадке, параллельной напряжению σ2, |
||||||||
|
τ2 = |
|
σ1 – σ3 |
. |
|
(4.16) |
||
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
На площадке, параллельной главному напряжению σ1, |
||||||||
|
τ3 = |
|
σ1 – σ2 |
. |
|
(4.17) |
||
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |

Наибольшее касательное напряжение действует по площадке, перпендикулярной второй главной площадке, наклоненной к двум другим главным площадкам под углом 45°, и равно
τmax = σ1 – σ3 .
2
4.4.2. Деформации при объемном напряженном состоянии
Рассмотрим деформацию бесконечно малого элемента с размерами ребер dx, dy, dz (рис. 4.8). По граням параллелепипеда действуют главные напряжения σ1, σ2, σ3. Вследствие де-
|
|
|
|
|
у |
σ2 σ3 |
формации длины ребер эле- |
||||
|
|
|
|
|
|
мента становятся |
равными |
||||
|
dz |
|
|
|
|
dx + ∆dx, dy + ∆dy, dz + ∆dz. |
|||||
|
|
|
|
σ1 |
Величины |
ε |
= ∆dx , |
||||
|
|
|
|
|
|
|
|||||
σ1 |
dy |
|
|
|
|
х ε2 = ∆dy , ε3 |
= ∆dz |
1 |
dx |
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
называ- |
|||||
|
|
|
|
|
dx |
|
|
dy |
dz |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
σ3 |
|
|
|
|
ются относительными удлине- |
|||
z |
|
|
|
|
σ2 |
||||||
|
|
|
|
|
ниями в направлении главных |
||||||
|
|
|
|
|
Рис. 4.8 |
напряжений, |
или |
главными |
|||
|
|
|
|
|
линейнымидеформациями. |
||||||
|
|
|
|
|
|
|
|
||||
Зависимость между линейными деформациями и главными напряжениями в общем случае трехосного напряженного состояния выражается обобщенным законом Гука:
ε = |
1 |
|
σ – µ (σ +σ ) |
, |
|
|||||||||
|
E |
|
||||||||||||
1 |
|
|
|
1 |
2 |
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
ε |
|
= |
1 |
|
σ |
|
– µ (σ +σ ) |
, |
(4.18) |
|||||
|
|
|
|
|
||||||||||
|
2 |
|
|
E |
|
2 |
1 |
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
ε |
|
= |
1 |
|
σ |
|
– µ (σ +σ |
|
) . |
|
||||
|
|
E |
|
|
|
|||||||||
|
3 |
|
|
|
|
3 |
1 |
|
2 |
|
|
|
||
Из формул (4.18) легко можно получить закон Гука для плоского напряженного состояния как частного случая объемнонапряженного состояния.
54

Объемная деформация. При упругой деформации тела изменяется его объем. Относительное изменение объема определяется по формуле
ε |
= |
V1 |
−V0 |
= ε + ε |
2 |
+ ε |
. |
(4.19) |
|
|
|||||||
V |
|
|
1 |
3 |
|
|
||
|
|
|
V0 |
|
|
|
|
|
Здесь V0 – объем элемента до деформации, V1 – объем элемента в деформированном состоянии. Выразив главные удлинения через главные напряжения при помощи формул(4.18), получим
ε |
= |
1−2µ |
(σ + σ |
2 |
+ σ |
3 |
). |
(4.20) |
|
||||||||
V |
|
E |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
4.4.3. Потенциальная энергия деформации
Потенциальной энергией деформации называется энергия, которая накапливается в теле при его деформации. В упругой области она численно равна работе внешних сил, затраченной на деформацию тела. Энергия, отнесенная к единице объема, называется удельной потенциальной энергией деформации. При простом растяжении
u = |
σε |
. |
(4.21) |
|
2 |
||||
|
|
|
Распространяя эту формулу на случай объемного напряженного состояния, получим выражение для полной удельной потенциальной энергии:
u = |
1 |
σ ε + |
1 |
σ |
|
ε |
|
+ |
1 |
σ |
ε |
|
. |
|
2 |
2 |
|
|
2 |
|
|||||||||
|
1 |
1 |
|
2 |
|
2 |
|
3 |
|
3 |
|
|||
Приподстановкевыраженийε1, ε2, ε3 изформул(4.18) получим: u = 21E σ12 + σ22 + σ32 – 2µ (σ1σ2 + σ2σ3 + σ3σ1 ) . (4.21, а)
При деформации элемента изменяется как его объем, так и форма. В соответствии с этим можно считать, что полная удельная потенциальная энергия деформации состоит из удельной потенциальной энергии изменения объема uоб и удельной потенциальной энергии изменения формы uф:
55
u = uоб +uф. |
(4.22) |
Удельная потенциальная энергия изменения объема определяется по формуле
u |
об |
= |
1−2µ |
(σ |
+ σ |
2 |
+ σ |
3 |
)2 . |
(4.23) |
|
||||||||||
|
|
6E |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Формула для определения удельной потенциальной энергии изменения формы имеет вид
u |
= |
1+µ |
(σ |
– σ |
2 |
)2 |
+(σ |
2 |
– σ |
3 |
)2 +(σ |
3 |
– σ |
)2 |
. (4.24) |
|
|
||||||||||||||||
ф |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
||||
|
|
6E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5.Гипотезы прочности
Взависимости от условий нагружения материал конструкции может находиться в различных механических состояниях. При небольших внешних силах возникают только упругие деформации (упругое состояние материала). При увеличении нагрузки на конструкцию обнаруживаются заметные остаточные деформации и материал находится в пластическом состоянии. Дальнейший рост нагрузки приводит к образованию местных трещин, и наступает состояние разрушения. Причем в различных напряженных состояниях свойства материала проявляются по-разному. Например, чугун, имеющий хрупкий характер разрушения при линейном нагружении, под действием большого всестороннего давления приобретает свойства пластичности.
Таким образом, механическое состояние материала в точке зависит, впервуюочередь, отнапряженного состояния вэтой точке.
Введем понятие предельного напряженного состояния. Предельным называется напряженное состояние, при котором происходит качественное изменение механического состояния материала.
Число, показывающее, во сколько раз следует увеличить все компоненты напряженного состояния, чтобы оно стало предельным, называется коэффициентом запаса прочности.
Экспериментальное определение совокупности предельных состояний в общем случае связано с большими трудностями. Это заставляет искать теоретические пути для оценки опасного напряженного состояния. Такие пути устанавливают так назы-
ваемые теории прочности.
56

Основная задача теорий прочности состоит в установлении условий начала текучести или разрушения материала при сложном напряженном состоянии на основании экспериментальных данных, полученных для того же материала при испытаниях на растяжение, сжатие или чистый сдвиг. Иначе говоря, задача состоит в установлении условий равноопасности различных напряженных состояний.
Напряженные состояния называются равноопасными, если для достижения предельных напряженных состояний их компоненты надо увеличить в одинаковое число раз, т.е. для них равны коэффициенты запаса.
При построении теорий предельного состояния принято исследуемое напряженное состояние сравнивать с одноосным растяжением, как наиболее типичным и легко осуществимым состоянием.
Напряжение в образце, подвергнутом осевому растяжению и находящемся в равноопасном с рассматриваемым элементом состоянии, называется эквивалентным напряжением и обозначается символом σэкв. Если σэкв достигает предела текучести или предела прочности при одноосном растяжении, то в элементе, находящемся в сложном напряженном состоянии, также начнется течение или разрушение материала. Если же σэкв будет меньше предельного напряжения σпр при одноосном растяжении, то рассматриваемый элемент и образец будут обладать одинаковым запасом прочности
σ
σэкв .
Вэтом случае условие прочности имеет вид
σэкв ≤ [σ], или n ≥ [n].n = пр
Ниже представлены пять теорий прочности, получивших наибольшее распространение в технике.
Первая теория прочности (теория наибольших нормальных напряжений)
Эта теория связывает разрушение материала с достижением наибольшим нормальным напряжением предельного значения.
57

Согласно данной теории, напряженные состояния будут равноопасными, если их наибольшие нормальные напряжения одинаковы.
Поскольку при сложном напряженном состоянии наибольшим нормальным напряжением является σ1, условие прочности будет иметь вид
σI |
=σ ≤[σ]. |
(4.25) |
экв |
1 |
|
Теория не получила подтверждения в целом ряде экспериментов. В ней не учитывается возможность появления пластических деформаций, поэтому она не применима для пластичных материалов и для напряженных состояний, приводящих к пластическим деформациям.
Теория иногда применяется при расчете конструкций из очень хрупких материалов (бетон, камень, кирпич).
Вторая теория прочности (теория наибольших относительных удлинений)
В этой теории в качестве критерия разрушения принято наибольшее относительное удлинение.
Теория утверждает, что напряженные состояния будут равноопасны, если для них равны наибольшие относительные удлинения.
Наибольшее относительное удлинение при трехосном напряженном состоянии согласно обобщенному закону Гука возникает в направлении первого главного напряжения:
εmax = ε1 = E1 [σ1 – µ(σ2 + σ3 )].
При эквивалентном одноосном напряженном состоянии
εmax = σэквE .
Условие прочности имеет вид
σII |
=σ – µ(σ |
2 |
+ σ |
3 |
) ≤[σ]. |
(4.26) |
экв |
1 |
|
|
|
58

Эта теория прочности так же, как и первая, применима к материалам в хрупком состоянии (высокопрочные инструментальные стали, чугун).
Третья теория прочности (теория наибольших касательных напряжений)
Согласно этой теории, напряженные состояния будут равноопасными, если их максимальные касательные напряжения равны.
Ввиду того, что при сложном напряженном состоянии эле-
мента τmax = σ1 – σ3 , а при одноосном растяжении образца
2
τmax = σэкв2 , условие прочности приобретает вид
σIII |
=σ – σ |
3 |
≤[σ]. |
(4.27) |
экв |
1 |
|
|
Третья теория дает хорошие результаты для пластичных материалов с одинаковым пределом текучести при растяжении
исжатии. Теория не применима для хрупких материалов или для напряженных состояний, приводящих к хрупкому разрушению.
Для материалов, неодинаково работающих на растяжение
исжатие, третья теория опытами не подтверждается. Существенным недостатком теории является то, что в ней
не учитывается влияние на прочность материала второго главного напряжения σ2.
Четвертая теория прочности (теория удельной потенциальной энергии изменения формы)
Согласно этой теории, напряженные состояния равноопасны, если для них равны удельные потенциальные энергии изменения формы.
При сложном напряженном состоянии удельная потенциальная энергия изменения формы определяется по выражению
uф = 16+Eµ (σ1 – σ2 )2 +(σ2 – σ3 )2 +(σ3 – σ1 )2 .
59

При |
одноосном |
растяжении |
образца, |
когда σ1 |
= σэкв, |
||||||||||||
а σ2 = σ3 = 0, |
u |
|
= |
1+µ |
2σ2 . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ф |
|
6E |
|
экв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда условие прочности имеет вид |
|
|
|
|
|||||||||||||
σIV |
= |
1 |
(σ – σ |
2 |
)2 +(σ |
2 |
– σ |
3 |
)2 +(σ |
3 |
– σ |
)2 |
≤[σ]. |
(4.28) |
|||
|
|
||||||||||||||||
экв |
|
2 |
|
1 |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теория дает хорошие результаты для пластичных материалов, одинаково работающих на растяжение и сжатие. Преимуществом четвертой теории перед третьей является то, что в ней учитывается влияние всех трех главных напряжений.
Теория прочности Мора
Данная теория прочности основана на результатах испытания при двух видах нагружении – растяжении и сжатии. Предполагается, что главное напряжение σ2 не влияет на механическое состояние материала, а ответственными за наступление предельного состояния являются напряжения σ1 и σ3.
Условие прочности имеет вид
σV |
=σ – kσ |
3 |
≤ [σ]. |
|
|
(4.29) |
экв |
1 |
|
|
|
|
|
Здесь коэффициент неравнопрочности k = |
σпчр |
, |
|
|||
|
|
|
|
σспч |
|
|
где σпчр – предел прочности при растяжении; σспч |
– предел |
|||||
прочности при сжатии.
Применяется данная теория прочности для материалов, поразному сопротивляющихся растяжению и сжатию.
4.6. Чистый сдвиг и его особенности
Чистым сдвигом называется такой случай плоского напряженного состояния, когда по двум взаимно перпендикулярным площадкам действуют только касательные напряжения (рис. 4.9).
60
