книги / Оптимальное проектирование конструкций.-1

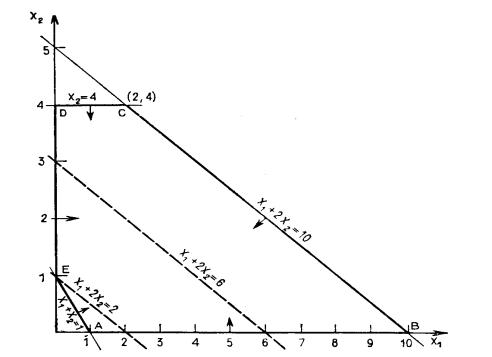
Пример 4.8. Найти х1 и х2 такие, чтобы z(x) = x1 + 2x2 max

при ограничениях

x1 + 2x2 ≤ 10; x1 ≥ 0; x1 + x2 ≥ 1;

x2 ≥ 0; x2 ≤ 4.

Допустимая область показана на рис. 4.11. Проведены прямые, соответствующие значениям z = 2; 6; 10.

Оптимальное значение целевой функции равно 10, причем соответствующая прямая x1 + 2x2 = 10 содержит отрезок ВС, лежащий на границе

допустимой области. Поэтому все точки на отрезке ВС представляют собой оптимальное решение.

Если в данном примере, например, убрать ограничение x1 + 2x2 ≤ 10 ,

то в этом случае удаление линии постоянного уровня критерия начала координат вызывает рост целевой функции и максимум z = ∞. В этом случае говорят, что задача линейного программирования имеет неограниченный оптимум.

81

В практических задачах такого варианта быть не должно, ибо это означает, что располагая конечным числом параметров (ресурсов), можно получить неограниченный доход. Это свидетельствует о том, что на этапе построения модели пропущено одно или несколько ограничений и, следовательно, необходимо вернуться к этому этапу.

Рассмотренные примеры позволяют выделить свойство, которое выполняется для всех задач линейного программирования: если в задаче ли-

нейного программирования существует оптимальное решение, то, по крайней мере, одна из вершин допустимой области представляет оптимальное решение.

На этом свойстве основан один из основных методов решения задач линейного программирования – симплекс-метод, идея которого заключается в переборе конечного числа вершин допустимой области. Например, в примере 4.7 нужно сосчитать значения z в трех вершинах допустимой области: z(А) = 377,6, z(В) = 680, z (С) = 480. Следовательно, минимальное

значение целевой функции будет в точке А с координатами х1 = 8 и х2 = 1,6,

а максимальное значение – в точке В с координатами х1 = 8 и х2 = 10. Аналогично в примере 4.8 значения целевой функции в вершинах z(А) = 1, z(В) = 10, z(С) = 10, z(А) = 380, z(D) = 8, z(E) = 2. Поскольку максимального значения функция достигает в вершинах В и С, то обе они представляют оптимальные решения.

Сформулированное ранее свойство является базовым в используемом для решения задач линейного программирования симплекс – методе. Для решения этим методом необходимо представить задачу в стандартной форме.

4.2.2. Стандартная форма задач линейного программирования

Задача линейного программирования в стандартной форме имеет вид: найти n переменных х, которые максимизируют или минимизируют функцию

z = c1x1 + c2 x2 + ... + cn xn

при ограничениях

a11x1 + a12 x2 + ... + a1n xn = b1;

a21x1 + a22 x2 + ... + a2n xn = b2 ;

…………………………………

am1x1 + am2 x2 + ... + amm xm = bm ;

m < n; xi ≥ 0 для всех i = 1, 2, ..., n.

82

Однако на практике ограничения часто бывают в виде неравенств, да и на переменные не всегда наложено требование неотрицательности. В этом случае необходимо провести следующие преобразования:

1. Преобразование неравенств: ограничение-неравенство преобразуется к ограничению-равенству путем введения так называемых остаточных или избыточных переменных. Например, неравенство вида x1 + 2x2 ≥ 5

можно преобразовать в равенство, если ввести новую неотрицательную переменную x3 :

x1 + 2x2 − x3 = 5 .

Если бы знак неравенства был обратный, то переменную x3 следовало бы добавить, т.е. неравенство x1 + 2x2 ≤ 5 перешло бы в равенство

x1 + 2x2 + x3 = 5 .

Значения дополнительных переменных в оптимальном решении позволяют судить о том, являются ли ограничения в виде неравенств активными.

2. Преобразование неопределенных по знаку переменных: если переменные по условию задачи могут принимать как положительное, так и отрицательное значение, то такие переменные следует заменить разностью двух неотрицательных переменных.

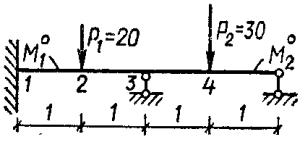
Пример 4.9. Оптимизация двухпролетной жестко-пластической балки. Заданы схема, размеры и нагрузка двухпролетной жестко-пластической неразрезанной балки (рис. 4.12). Каждый из элементов балки имеет постоянное по длине прямоугольное сечение, определяемое пластическими мо-

ментами М10 и М20 . Требуется так

подобрать значения М10 и М20 ,

чтобы добиться минимума веса конструкции в условиях упругопластической работы.

Р е ш е н и е . Примем вес балки пропорциональным предельным пластическим моментам (при которых сечение полностью пере-

ходит в пластическое состояние) и длинам стержней, тогда критерий качества

z = 2M10 + 2M 20 min .

Согласно теореме предельного равновесия А.А. Гвоздева конструкция не разрушится, если существуют такие значения моментов, которые

83

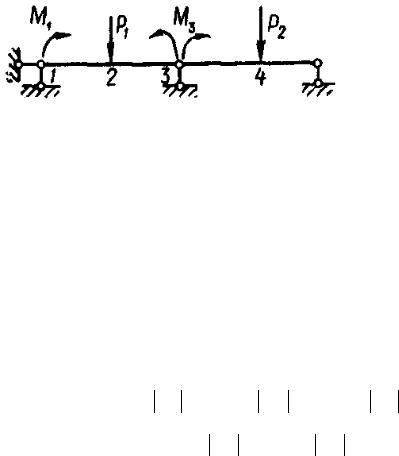
зуя метод сил, отбросим две лишние связи, т.е. введем идеальные шарниры в опорах 1 и 3 и лишние неизвестные моменты М1 и М2 (рис. 4.13).

Согласно уравнениям равновесия максимальные пролетные моменты

Условия пластичности в опасных сечениях имеют вид

М1 ≤ М10 ; М2 ≤ М10 ; М3 ≤ М10 ; М3 ≤ М20 ; М4 ≤ М20.

Для опоры 3 сформулированы два условия пластичности, ибо заранее неизвестно, сечение какого стержня в оптимальном варианте окажется слабее.

Приведем формулировку задачи к стандартной форме. Так как моменты над опорами, очевидно, отрицательны, а в опасных сечениях положительны, то введем новые положительные переменные т1 ≥ 0 и т2 ≥ 0

( m1 = −M1; m2 = −M 2 ).

Тогда, переходя от двухсторонних ограничений к односторонним с учетом условий равновесия, получим

Пять приведенных ограничений (a, d, f, h, k) выполняются тождественно (не активны), поэтому из дальнейшего рассмотрения будут исклю-

84

чены. Оставшиеся пять имеют вид неравенств, поэтому введем новые (искусственные) неотрицательные переменные у1 , у2 , у3 , у4 , у5 . Теперь

можно записать стандартную форму задачи линейного программирования:

М20 − m3 − y4 = 0; 2М20 + m3 − y5 = 30.

4.2.3.Симплекс-метод решения задач линейного программирования

Симплекс-метод применим для стандартной постановки задачи линейного программирования: найти

такие, чтобы

n

z = ∑ ci xi max (4.18)

i =1

при ограничениях

n

∑ a ji xi = b j ( j =1, ..., m) . (4.19)

i =1

Система (4.19) – система линейных алгебраических уравнений, решение которой определяет характер решения задачи в целом. Если система (4.19) не имеет решений, то задача теряет смысл; если существует единственное решение, то оно одновременно является и решением задачи, поскольку нет другого выбора. Если, наконец, система (4.19) имеет более одного решения, удовлетворяющего условию (4.17), то рассматриваемая задача становится объектом исследования. Как правило, m < n , а потому число решений бесконечно. Идея заключается в том, что система (4.19) ка- ким-либо методом, например, Гаусса–Жордана, приводится к каноническому виду, т.е. когда переменные х1, х2 , ..., хm входят в каждое из урав-

нений с коэффициентом 1, т.е. система (4.19) преобразуется к виду

85

Переменные х1, х2 , ..., хm называются зависимыми. Если переменным хm+1, хm+ 2 , ... хn придавать различные значения, то получим различные значения для переменных х1, х2 , ..., хm , поэтому переменные хm+1, хm+ 2 , ..., хn называются независимыми. Если независимые перемен-

ные приравнять нулю и при этом ~ ≥ то получим допустимое решение b j 0 ,

(все ограничения выполнены и зависимые переменные не отрицательны), которое называется базисным. Отметим, что в качестве зависимых переменных не обязательно должны быть выбраны первые m переменных.

Ранее было показано, что если оптимальное решение существует, то хотя бы одна из вершин допустимой области оптимальна. Доказано, что любая вершина допустимой области соответствует некоторому базисному решению. Тогда интуитивный путь решения заключается в нахождении всех допустимых базисных решений и последующем переборе всех решений с целью отыскания оптимальных.

Ясно, что это не самый эффективный путь, что гораздо лучше перебирать не все решения, а только те, которые улучшают показатель качества. На этом и основан симплекс-метод решения (исторически название метода связано с тем, что в одном из первых примеров, решенных этим методом, участвовало ограничение х1 + х2 + ... + хn ≤ 1, которое определяет сим-

плекс-обобщенный тетраэдр в n-мерном пространстве, отсекающий на осях единичные отрезки).

Симплекс-метод представляет собой итеративную процедуру, алгоритм которой включает следующие основные шаги:

1)приведение исходной задачи к стандартной форме и выбор начального допустимого базисного решения (все независимые переменные равны нулю, а зависимые положительны);

2)проверка полученного решения на оптимум;

3)переход от начального решения к другому базисному решению с лучшим значением целевой функции, если предыдущее решение оказалось не оптимальным;

4)повторение операций до тех пор, пока не будет получено оптимальное решение или подтверждение возможности неограниченного изменения функции.

86

Рассмотрим второй шаг алгоритма: чтобы оценить, является ли полученное решение оптимальным, необходимо выразить функцию цели через независимые переменные. Пусть независимыми переменными являются хm+1, хm+ 2 , ..., хn и функция цели записана в виде

нимума).

Пусть решение оказалось не оптимальным. Чтобы перейти к другому базисному решению, гарантирующему наибыстрейшее возрастание целе-

симально по модулю (обозначим через р этот номер i), в число зависимых, при этом какое-то зависимое переменное нужно перевести в разряд независимых. Этот перевод реализуем из условия положительности всех зависимых переменных. Если хр ≠ 0 , то

Рассмотрим отношение bk / akp , и то из переменных, у которого это

отношение минимально, следует перевести в разряд независимых переменных (правило минимального отношения).

Пример 4.10. Решим задачу, предложенную в примере 4.9, сим- плекс-методом.

Первый шаг – нахождение первого базисного решения из ограничений (4.16) с учетом того, что все переменные положительны:

М10 − m1 − y1 = 0;

2М10 + m1 + m3 − y2 = 20;

М10 − m3 − y3 = 0;

М20 − m3 − y4 = 0;

2М20 + m3 − y5 = 30.

Если принять в двух последних уравнениях в качестве независимых переменных y4 и y5 , то

87

что соответствует требованию допустимости решения. Аналогично из первого и третьего уравнений следует

Отрицательный знак у одной независимой переменной ( y4 ) означа-

ет, что найденное решение не является оптимальным. Переведем эту переменную в разряд зависимых, т.е. найдем решение, при котором y4 ≠ 0 . Это

можно сделать, обратив в ноль какую-либо из зависимых переменных. Анализ уравнений показывает, что в качестве кандидатов можно рассмат-

ривать переменные М10 , m1 и y2 . Если приравнять нулю M10 или m1 , то y2

будет отрицательным, что невозможно по требованию допустимости, следовательно, нулевой переменной может быть только y2 . Тогда

решение на оптимальность, для чего запишем целевую функцию через независимые переменные:

88

Так как коэффициенты всех независимых переменных положительны, то найденное решение является минимальным ( zmin = 35 ). Значения

оптимальных моментов: М1 = −5;

М3 = −5; М2 = 5; М4 = 12,5. Эпю-

ра моментов в оптимальной неразрезанной балке представлена на рис. 4.14.

Часто решение задач линейного программирования проводят симплекс-методом с помощью таб-

лиц. Однако в настоящее время существуют широко известные математические пакеты (EXELL, Mathcad и др.), в которых встроены блоки сим- плекс-метода, поэтому главное внимание следует уделять правильной постановке задачи и представлять ее в требуемой форме. Рассмотрим еще ряд задач.

Пример 4.11. Оптимизация веса фермы. Задана схема, размеры и нагрузка симметричной фермы с одной лишней связью (рис. 4.15). С целью упрощения расчетное сопротивление принято одинаковым для растянутых и сжатых стержней. Требуется найти наилегчайшую статически определимую ферму, которая может быть получена из заданной путем устранения лишнего стержня.

Р е ш е н и е . Вес заданной фермы

Условием прочности является

σ i = Ni / Fi ≤ σ 0 ,

где σ i , Ni – напряжение и усилие в i-м стержне; σ 0 − предельное напряжение. Так как Fi ≥ 0 , то условие прочности можно записать в виде двух

эквивалентных неравенств:

Ni ≥ −σ 0 Fi ; Ni ≤ σ 0 Fi .

89

По условию задачи искомая ферма статически определима, поэтому усилия должны быть подчинены только условиям равновесия. Рассмотрев равновесие узлов А и С, получим

N4 = −0,634N1 − P.

С учетом уравнений равновесия целевая функция и условия прочности примут вид

z = G / γ = 12,64F1 +12,06F2 +12F3 + 2,6F4 ;

Перейдем от ограничений неравенств к ограничениям равенств путем введения новых искусственных переменных уi и Yi ( i = 1, 2, 3, 4) .

90