
книги / Математика. Линейная алгебра, векторная алгебра, аналитическая геометрия-1
.pdf
Основные формулы |
|
Определения и замечания |
|||||||
и рисунки |
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
мого прямой на оси OY |
или |
||
|
|
|
|
|
|
начальная ордината. |
|
||
|
|
|
|
|
|
Замечание. Уравнение прямой |
|||
|
|
|
|
|
|
с угловым коэффициентом раз- |
|||
|
|
|
|
|
|
решено относительно текущей |
|||
|
|
Рис. 3 |
|
координаты y. |
|
|
|||
|
|
|
|
|
|
|
|||
где k = tg ϕ – угловой коэффи- |
|
|
|
|
|||||
циент (рис. 3). |
|
|
|
|
|
|
|
||
5. Уравнение прямой в отрезках |
Следует запомнить, что |
а – |
|||||||
(рис. 4) |
|
|
|
величина отрезка, |
отсекаемого |
||||
|
x |
+ |
y |
= 1 . |
(5) |
прямой на оси OX ; b – вели- |
|||
|
|
|
чина |
отрезка, |
отсекаемого |
||||
|
a |
b |
|
||||||
|
|
|
|
|
|
прямой на оси OY. |
|
|
|
|
|
|
|
|
|
Замечание. |
|
|
|
|
|
|
|
|
|
Особенности этого уравнения |
|||
|
|
|
|
|
|
такие: в левой части уравнения |
|||
|
|
|
|
|
|
между |
дробями |
стоит |
знак |
|
|
|
|
|
|
плюс, величины a и b могут |
|||
|
|
|
|
|
|
быть как положительными, так |
|||
|
|
Рис. 4 |
|
и отрицательными, правая часть |
|||||
|
|
|
уравнения равна единице. |
|
|||||
|
|
|
|
|
|
|
|||
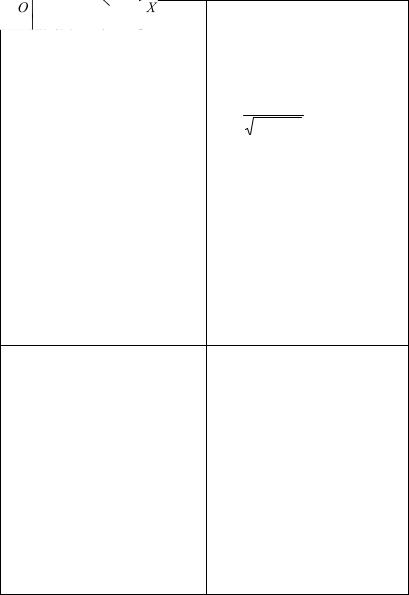
6. Нормальное |
уравнение |
пря- |
p – длина перпендикуляра, |
||||||
мой (рис. 5): |
|
|
|
опущенного из начала коорди- |
|||||
x cos α + y sin α − p = 0. |
(6) |
нат на прямую; α – угол, кото- |
|||||||
|
|
|
|
|
|
рый образует этот перпендику- |
|||
|
|
|
|
|
|
ляр |
|
|
|
|
|
|
|
|
|
с положительным направлени- |
|||
|
|
|
|
|
|
ем оси OX . |
|
|
|
|
|
|
|
|
|
Следует запомнить: для при- |
|||
|
|
|
|
|
|
ведения |
общего |
уравнения |
|
91
Основные формулы |
Определения и замечания |
|||||||
и рисунки |
||||||||
|
|
|
|
|
|
|
||
|
прямой |
к |
|
нормальному виду |
||||
|
обе его части надо умножить |
|||||||
|
на нормирующий |
множитель |
||||||
|
µ = ± |
1 |
, |
причем перед |
||||
|
|
|
||||||
|
A2 + B2 |
|
|
|
||||
|
дробью следует выбрать знак, |
|||||||
|
противоположный |
знаку сво- |
||||||
Рис. 5 |
бодного |
|
члена |
С |
в |
общем |
||
уравнении прямой. |
|
|
||||||
|
|
|
||||||
|
Замечание. Особенности нор- |
|||||||
|
мального |
|
уравнения |
прямой: |
||||
|
сумма квадратов коэффициен- |
|||||||
|
тов при текущих координатах |
|||||||
|
равна |
единице, |
|
свободный |
||||
|
член отрицателен, а правая |
|||||||
|
часть его равна нулю. |
|
||||||
7. Уравнение прямой, проходящей через данную точку A(x1, y1 ) в данном направле-
нии, |
определяемом |
угловым |
||||
коэффициентом k, |
|
|
||||
|
|
y − y1 = k(x − x1 ). |
(7) |
|||
8. Уравнение прямой, |
проходя- Текущие координаты – это |
|||||
щей |
через две данные |
точки координаты переменной точки |
||||
А(x1, y1 ) и В(x2 , y2 ): |
|
прямой. |
||||
|
|
y − y1 |
= |
x − x1 |
, |
(8) |
|
|
y2 − y1 |
x2 − x1 |
|||
|
|
|
|
|
||
(x, y)− текущие координаты. |
||||||
92

Основные формулы |
Определения и замечания |
||||||||||
и рисунки |
|
||||||||||
|
|
|
|
|
|
||||||
Угловой коэффициент прямой, |
|
|
|
|
|
||||||
проходящей через две данные |
|
|
|
|
|
||||||
точки |
|
|
|
|
|
|
|||||
k = |
|
y2 − y1 |
. |
(9) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
x2 − x1 |
|
|
|
|
|
|
|||
9. Если две прямые |
заданы Углом |
между |
прямыми |
(I) |
|||||||
уравнениями с угловым коэф- и (II) (рис. 6), рассматривае- |
|||||||||||
фициентом |
|
мыми в указанном порядке, |
|||||||||
y = k1x + b1, |
|
будем называть тот угол, на |
|||||||||
y = k2 x + b2 , |
|
который нужно повернуть пря- |
|||||||||
то угол между ними θ (рис. 6) |
мую (I), |
чтобы |
она совпала |
||||||||
определяется по формуле |
с (II) (или стала ей параллель- |
||||||||||
tg θ = |
k2 − k1 |
. |
(10) |
на). |
|
|
|
|
|||
Замечание 1. |
Если речь |
идет |
|||||||||
|
|||||||||||
|
1+ k1k2 |
|
об угле между двумя прямыми |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
и не указан порядок, в котором |
|||||
|
|
|
|
|
|
они рассматриваются, то мож- |
|||||
|
|
|
|
|
|
но устанавливать этот порядок |
|||||
|
|
|
|
|
|
произвольно. Очевидно, изме- |
|||||
|
|
|
|
|
|
нение порядка повлечет за со- |
|||||
|
|
|
|
|
|
бой изменение знака для тан- |
|||||
|
|
|
|
|
|
генса угла. |
|
|
|
||
|
|
|
|
|
|
Замечание 2. |
В |
формуле |
для |
||
Рис. 6 |
|
вычисления |
tg θ знак «+» со- |
||||||||
|
ответствует острому углу θ, |
||||||||||
|
|
|
|
|
|
||||||
Если уравнения прямых заданы а знак «–» – тупому. |
|
||||||||||
в общем виде: |
|
|
|
|
|
|
|||||
A1x + B1 y + C1 = 0, A2 x + B2 y + C2 = 0,
угол между ними определяется
93

|
Основные формулы |
|
Определения и замечания |
||||||||||||||
|
|
|
|
|
|
и рисунки |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
по формуле |
|
|
|
|
|
|
|||||||||||
|
|
|
tg θ = |
A1B2 − A2 B1 |
. |
(11) |
|
||||||||||
|
|
A1 A2 + B1B2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||||||||
10. |
Пусть две прямые |
заданы |
Следует запомнить: |
||||||||||||||
уравнениями общего вида: |
|
если прямые пересекаются, т.е. |
|||||||||||||||
|
|
|
A1x + B1 y + C1 = 0, |
|
(12) |
имеют одну общую точку, то |
|||||||||||
|
|
|
A2 x + B2 y + C2 = 0. |
|
координаты этой точки долж- |
||||||||||||
Возможны три случая: |
|
|
ны удовлетворять обоим урав- |
||||||||||||||
|
|
нениям (12). |
|||||||||||||||
|
A1 |
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
а) |
|
≠ |
|
|
|
− прямые пересека- |
Следовательно, для нахожде- |
||||||||||
A2 |
|
B2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ния координат точки пересече- |
||||
ются; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния прямых нужно решить со- |
||
б) |
A1 |
|
= |
|
|
B1 |
|
≠ |
C1 |
– прямые па- |
вместно их уравнения. |
||||||
A2 |
|
|
|
B2 |
C2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
раллельны; |
|
|
|
|
|
|
|
|
|
||||||||
в) |
A1 |
|
= |
B1 |
|
= |
C1 |
− прямые |
сов- |
|
|||||||
|
|
|
|
|
|||||||||||||
|
A2 |
|
|
|
|
B2 |
|
|
|
C2 |
|
|
|
|
|||
падают. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11. Если две |
прямые |
заданы |
|
||||||||||||||
уравнениями с угловым коэф- |
|
||||||||||||||||
фициентом |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
y = k1x + b1 , |
|
|
|
||||||||
|
|
|
|
|
|
y = k2 x + b2 , |
|
|
|
||||||||
то прямые: |
|
|
|
|
|
|
|
|
|
||||||||
а) параллельны, если |
|
|
|
||||||||||||||
|
|
|
|
k1 = k2 , b1 ≠ b2 ; |
|
(13) |
|
||||||||||
б) перпендикулярны, если |
|
|
|||||||||||||||
|
|
|
|
|
|
k1 k2 = −1. |
|
(14) |
|
||||||||
12. Расстояние от точки A(x1, y1 ) |
Расстояние от точки A(x1; y1 ) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
94
Основные формулы |
|
Определения и замечания |
|||
|
и рисунки |
|
|||
|
|
|
|||
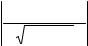
до прямой Ax + By + C = 0 |
|
до прямой Ax + Bx + C = 0 есть |
|||
d = |
Ax1 |
+ By1 + C |
|
длина перпендикуляра, опу- |
|
(15) |
щенного из этой точки на пря- |
||||
|
. |
||||
|
|
A2 + B2 |
|
мую. |
|
|
|
|
|
||
Задачи
Задача 1. Прямая задана уравнением 2x + 3y − 5 = 0. Лежат
|
|
|
1 |
|
ли на ней точки A(–2; 3), B(1; 1), |
C |
− |
|
; − 2 ? |
|
||||
|
|
|
2 |
|
Решение.
Проверим, лежат ли на данной прямой точки A, B и C.
A (–2; 3), |
|
|
2 (− 2)+ 3 3 − 5 = 0, |
A лежит на прямой. |
||||||
B (1;1), |
|
|
2 1 + 3 1 − 5 = 0, B лежит на прямой. |
|||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
C − |
|
; − 2 |
|
, |
2 |
− |
|
+ 3(− 2)− 5 |
≠ 0, C не |
лежит на пря- |
|
|
|||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
мой. |
|
|
|
|
|
|
|
|
|
|
Задача 2. |
|
|
|
|
|
|
|
|
||
Построить прямые: |
|
|
|
|
||||||
а) 2x − 4y + 1 = 0 ; б) x − 3y = 0; |
|
|
||||||||
в) 3x + 5 = 0; |
|
г) 2y − 3 = 0. |
|
|
||||||
Решение. |
|
|
|
|
|
|
|
2x − 4y + 1 = 0 |
||
а) Определим точки |
пересечения прямой |
|||||||||
с координатными осями. Взяв в этом уравнении сначала |
y = 0, |
||||||
найдем из него, что точка |
A пересечения прямой с осью OX |
||||||
|
1 |
|
|
|
1 |
|
|
имеет абсциссу x = − |
|
. Координаты точки A |
− |
|
; 0 . |
Поло- |
|
|
|
||||||
|
2 |
|
|
|
2 |
|
|
жив теперь в уравнении x = 0, найдем, что точка B пересечения
95

прямой с осью OY имеет ординату y = 1 . Координаты точки
|
|
4 |
|
1 |
|
B 0; |
|
. Построив эти точки, соединим их прямой. Эта прямая |
|
||
|
4 |
|
и соответствует данному уравнению (рис. 7).
Рис. 7
Эту задачу можно решить другим методом, используя уравне-
ние (5).
Перенося свободный член данного уравнения в правую часть равенства, получим
2x − 4y = −1.
Деля обе части равенства на (–1), будем иметь:
2x |
+ |
− 4y = 1 |
x |
|
+ |
y |
= 1 |
|||
|
|
1 |
|
|
||||||
− 1 |
− 1 |
|
− |
|
1 |
|
||||
|
|
|
|
|
2 |
4 |
|
|||
|
|
|
|
|
|
|
||||
|
|
a = − |
1 |
– на оси OX ; |
||||||
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
96

b = 1 – на оси OY. 4
б) Прямая x − 3y = 0 проходит через начало координат (C = 0), поэтому для ее построе-
ния достаточно найти еще только одну точку, принадлежащую ей.
Взяв |
x = 3, получим, что |
y = 1 |
||
и, значит, точка A (3;1) принад- |
||||
лежит прямой (рис. 8). |
|
|||
в) Уравнение 3x + 5 = 0 |
пере- |
|||
пишем в виде x = − |
5 |
. Это урав- |
||
|
||||
|
3 |
|
|
|
нение |
определяет прямую, |
у ко- |
||
торой все точки имеют абсциссы,
|
|
5 |
|
равные |
− |
|
(рис. 9). |
|
|||
|
|
3 |
|
г) Уравнение 2y − 3 = 0 пе-
репишем в виде y = 3 . 2
Это уравнение определяет прямую, у которой все точки имеют
ординату равную 3 (рис. 10). 2
Рис. 8
Рис. 9
Рис. 10
Задача 3. Составить уравнение прямой, которая отсекает на отрицательной полуоси OY отрезок, равный 3 единицам, и об-
разует с осью OX угол π . 6
Решение.
Прямая пересекает ось OY в точке B(0; − 3) и имеет угло-
вой коэффициент k = tg ϕ = tg π = |
3 . Полагая в уравнении (4) |
6 |
3 |
97
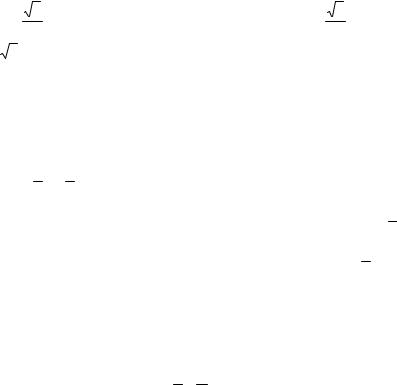
k = 3 и b = −3, получим искомое уравнение y = |
3 x − 3 или |
3 |
3 |
3x − 3y − 9 = 0. |
|
Задача 4. Написать уравнение с угловым коэффициентом для прямой линии, заданной уравнением 2x + 3y + 7 = 0.
Решение.
Разрешив данное уравнение относительно y, получим
y = − 2 x − 7 . 3 3
Отсюда следует, что угловой коэффициент прямой k = − 2 , 3
а величина отрезка, отсекаемого ею на оси ординат, b = − 7 . 3
Задача 5. Составить уравнение прямой, проходящей через точку А(2; 5) и отсекающей на оси ординат отрезок b = 7.
Решение.
Будем искать уравнение прямой в виде (5):
x + y = 1. a b
Согласно условию задачи b = 7. Прямая проходит через точку А(2; 5), следовательно, координаты точки удовлетворяют данному уравнению.
Получаем
|
2 |
+ |
5 |
= 1 , |
|
а = 7. |
|||
|
|
|
|||||||
|
a 7 |
|
|
|
|
|
|
||
Искомое уравнение прямой |
|
x |
+ |
y |
= 1 или x + y − 7 = 0. |
||||
|
|
|
|||||||
|
|
|
|
7 |
7 |
|
|||
Задача 6. Уравнение прямой линии 3x + 4y + 15 = 0 привести к нормальному виду.
98

Решение. |
|
|
Составим нормирующий множитель µ = ± |
1 |
= ± 1 . |
|
32 + 42 |
5 |
В нашем случае свободный член в общем уравнении равен +15, а поэтому нормирующий множитель имеет знак минус. Умно-
|
|
1 |
|
|
|
жая на |
− |
|
обе части уравнения 3x + 4y + 15 |
= 0, |
приведем его |
|
|||||
|
|
5 |
|
|
|
к нормальному виду:
|
|
|
|
− |
3 |
x − |
4 |
y − 3 = 0 . |
|
|
|
5 |
|||||
|
|
5 |
|
|
||||
Для |
данной прямой, |
следовательно, имеем: p = 3, |
||||||
cos α = − |
3 |
, sin α = − |
4 |
. |
|
|
||
|
|
|
|
|||||
5 |
5 |
|
|
|
|
|
||
Задача 7. Найти уравнение прямой по следующим условиям: ее расстояние от начала координат равно 7 единицам длины и угол между осью OX и перпендикуляром к искомой прямой, проведенный из начала координат, равен 120°.
Решение.
Будем искать уравнение прямой в виде (6). Согласно усло-
вию задачи cos α = cos120° = − |
1 |
, sin α = |
3 , ρ = 7. |
|
|||
2 |
|
2 |
|
Подставляя эти значения в уравнение (6), получим искомое уравнение прямой
− 1 x +  3 y − 7 = 0 или x −
3 y − 7 = 0 или x −  3y + 14 = 0 . 2 2
3y + 14 = 0 . 2 2
Задача 8. Найти уравнение прямой, проходящей через точку A(1; 2) и наклоненной к оси абсцисс под углом в 45°.
99
Решение.
Угловой коэффициент прямой k = tg 45° = 1. Поэтому, воспользовавшись уравнением (7), получаем
y − 2 = 1(x − 1) или x − y + 1 = 0.
Задача 9. Найти острый угол между прямыми x − 3y + 5 = 0
и 2x + 4y − 7 = 0.
Решение.
Поставим перед собой задачу: найти острый угол между данными прямыми. Воспользуемся формулой (10), причем, поскольку нас интересует острый угол, правую часть форму-
лы (10) возьмем по абсолютной величине: tg θ = |
k2 − k1 |
|
. |
|||||||||||||||||
1+ k1k2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
1 |
|
|
|
|
− |
− |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||
У нас k1 = |
, |
k2 = − |
, |
tg θ = |
|
|
|
|
2 |
= 1, |
откуда θ = 45°. |
|||||||||
3 |
2 |
|
1− |
|
1 |
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
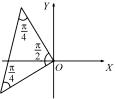
Задача 10. Составить уравнения прямых, проходящих через начало координат и образующих с прямой 3x − y + 5 = 0
угол θ = π . 4
Решение.
Уравнения искомых прямых имеют вид
|
y = kx, т.к. прямые проходят через начало |
|
координат. Задача имеет два решения (рис. |
|
11). Пусть угловой коэффициент одной из |
|
искомых прямых равен k. Угловой коэффи- |
|
циент заданной прямой равен 3. Поскольку |
Рис. 11 |
угол между этими прямыми равен π , |
|
4 |
100
