
книги / Прикладной статистический анализ в горном деле (Многомерная математическая статистика)
..pdf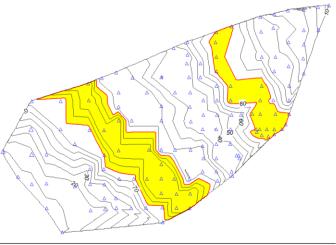
ными критериями исследователя. Такое суждение в большей части достоверно только для способов дискриминации, поскольку в технологиях кластеризации группирование объектов выполняется с использованием выбранных мер близости. Результаты кластеризации в значительной степени зависят от метрики, выбор которой обычно остаётся за специалистом. В помощь ему могут послужить имеющиеся в литературе рекомендации к выбору мер близости для разных задач [40; 46].
Рис. 2.2. Выделение зон с использованием изолиний
Принято считать, что термин «кластерный анализ» произошёл от английского слова cluster, которое переводится как гроздь, скопление. В 1939 г. Роберт Трион определил основную задачу кластерного анализа – разложение множества исследуемых объектов и переменных на однородные по каким-либо принципам группы [40; 50]. В настоящее время методология кластеризации предполагает не только разделение объектов на схожие сообщества, но и решает задачи раскрытия структуры связей в новых образованиях [40].
21
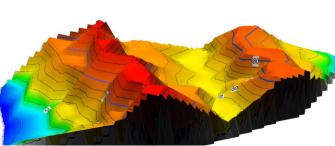
Рис. 2.3. Выделение зон в трёхмерном представлении рельефа
Преимущество этой методологии анализа заключается в том, что исследователь получает инструмент декомпозиции объектов не по одной измеренной переменной, а по всей совокупности входных признаков. Например, если имеются пробы с содержанием полезного компонента и мощности на плане горных работ, можно установить границу некондиционных запасов, группируя пробы одновременно по этим параметрам. Помимо отмеченного преимущества, кластерный анализ не накладывает каких-либо ограничений на характеристики изучаемых объектов при условии их нормирования, позволяя учитывать в анализе всю общность исходных данных практически произвольной природы [29]. В ряде случаев на рудниках возникает необходимость в группировании проб, имеющих геопространственные данные (координаты X, Y, Z), совместно с результатами химического анализа (KCl, NaCl, MgCl2 и др.). В некоторых случаях их будут дополнять результаты геомеханических или иных испытаний. И все эти разнородные по типу переменные могут быть учтены в процессе разбиения объектов на группы в кластерном анализе.
При анализе больших объемов информации кластеризация сжимает их. Такое свойство кластерного анализа особенно необходимо в ходе изучения объектов, имеющих пространственное расположение. На основе этой технологии можно формировать зоны распределения признаков (к примеру, зоны замещений), объединять в кластеры отдельные схожие участки
22
временных рядов или обрабатывать другие многомерные конструкции.
В горной промышленности решение ряда задач производится в геопространстве. Например, прогноз содержания хлористого калия и нерастворимого остатка на неосвоенный участок пласта. Или прогноз выбросов газа на территорию разработки в процессе планирования горных работ. В таких условиях появляется возможность совмещения кластерного анализа с другими распространёнными методами (к примеру, с использованием нейронных сетей, кореляционно-регрессионным анализом и другими технологиями).
Безусловно, как и другим статистическим методам, кластерному анализу присущи недостатки и ограничения [40]. К недочётам метода относят возможность лишения самобытных характеристик у отдельных объектов. Такое наблюдается, когда их измеренные значения подменяются некоторыми обобщенными характеристиками. В процессе необдуманного использования кластерного анализа к исходному массиву данных результаты вычислений могут исказить начальные параметры. Количество кластеров и их состав во многом будут зависеть от используемых параметров (критериев) расчленения множества объектов. По изложенной причине, используя кластерный анализ, принимается концепция о том, что используемые в анализе характеристики объектов классификации в принципе допускают возможность выполнить разбиение на кластеры. Этому будет способствовать и корректный отбор переменных для анализа, значения которых нормированы (говорят, выбраны переменные одного масштаба).
Для кластерного анализа проблема в ненормированных данных имеет особое значение. Оно заключается в том, что, к примеру, координаты скважин могут быть представлены в десятках тысяч метров, а химический анализ в долях процента. При расчётах дистанции в многомерном пространстве между объектами координаты геопространства, имеющие большие значения, будут иметь большие разности, а разности химических компонентов будут малы. По величине разности координа-
23
ты будут полностью доминировать над разностями химических компонентов, поэтому становится невозможно корректно вычислить дистанцию между объектами.
В связи с этим в кластерном анализе особенно важно нормировать переменные, причём метод нормирования использовать таким, чтобы среднее у всех переменных равнялось нулю, а среднее квадратическое отклонение – единице. Методы нормирования, приводящие к таким результатам, рассмотрены в работах [1; 61]. Вместе с тем единая позиция по вопросу о необходимости нормирования данных в кластерном анализе пока не сложилась [44]. Причиной тому является мнение о том, что «процедура нормирования, приводящая переменные к единичной дисперсии и нулевому среднему, уменьшает различия между группами по тем переменным, которые до преобразования предлагали лучшие групповые различия» [44]. По мнению авторов, будет предпочтительнее проводить нормирование внутри кластеров. С другой стороны, пока не проведены необходимые вычисления, а объекты не сгруппированы и кластеры не сформированы, это невозможно выполнить [44].
Основная задача кластерного анализа заключается в том, «чтобы на основании данных, содержащихся во множестве Х, разбить его элементы xi (i = 1, n) на m (j = 1, m, где m – целое) кластеров (подмножеств) Q1, Q2 , ... Qm , так, чтобы каждый
объект xi принадлежал одному и только одному подмножеству
разбиения j. А объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными» [40; 50].
Во время разделения всего имеющегося множества данных на группы, предварительно требуется отобрать какой-либо из имеющихся в программах критерий оптимального связывания объектов, наиболее подходящий для данных условий. Критерий обычно представляет собой некоторую математическую функцию, выражающую ожидаемые уровни желательных разбиений. Эту функцию называют целевой функцией [40; 50]. Поскольку каждый кластер формируется из наиболее близких объ-
24
ектов и может быть представлен в виде облака в многомерном пространстве, в прикладных программах в качестве такой функции может использоваться внутригрупповая сумма квадратов отклонения:
n |
|
|
2 |
n |
|
1 |
|
n |
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
, |
(2.2) |
||||||
W n x j x |
|
x2j |
|
x j |
|||||||
j 1 |
|
j 1 |
|
n |
|
j 1 |
|
|
|
||
где x j представляет собой измерения j-го объекта.
Соответственно, у этого облака имеется центр, разброс его объектов определяется среднеквадратическим отклонением и не выходит за предельный радиус, имеется и размер кластера
[40; 50].
Центр множества представляет среднее геометрическое положение точек в пространстве переменных. Величина радиуса кластера отражает максимальное удаление периферийных точек множества от центра кластера. Для корректного разделения данные должны быть представлены в едином диапазоне значений (нормированы).
Когда формируются кластеры, они могут и перекрываться, накладываясь друг на друга. В этом случае одна точка может принадлежать двум кластерам и невозможно однозначно отнести этот объект к одной из групп. Такие объекты будут спорными, и по количественной мере сходства они могут быть отнесены к нескольким кластерам.
Размер кластера определяется по радиусу кластера. Поскольку среднее значение нормированных переменных равно нулю, а дисперсия у них может отличаться, то радиус иногда определяется по дисперсии для этого кластера [40]. Определить принадлежность спорных объектов к кластерам могут профильные эксперты или аналитики.
В некоторых программных продуктах используется возможность присвоения весового множителя каждой из переменных. Такая возможность позволяет повлиять на значимость той или иной переменной с учётом мнения исследователя. Помощь в таком вопросе также могут оказать экспертные оценки, полу-
25
ченные специалистами исследуемой предметной области. Весовые множители позволяют получать меру близости между объектами в многомерном пространстве с учетом учитываемой важности переменных. Необходимость использования весовых коэффициентов устанавливается в ходе нескольких вариантов расчёта, сравнения полученных результатов и выбора лучшего из них.
2.2. Меры близости объектов
Итак, в методологии кластерного анализа используется объединение сходных между собой объектов. Именно поэтому понятие сходства (или близости) играет для него важную роль.
Впроцессе проведения анализа для количественной оценки похожести используется понятие метрики, или расстояния (distance), между объектами. Метрика представляет математическую модель сходства или различия объектов, которое устанавливается между классифицируемыми объектами. Чаще всего эта мера использует метрическое расстояния между объектами, и чем меньше это расстояние, тем больше сходство между ними. Если каждый объект описывается двумя или тремя переменными, в первом случае он может быть представлен как точка на плоскости, и сходство с другими объектами можно определить по кратчайшему расстоянию между ними (оно будет соответствовать евклидову расстоянию) [11; 15]. Во втором случае расстояние потребуется вычислять в трёхмерном пространстве. Аналогичный приём используют горные инженеры при решении своих задач на планах, группируя по пласту территориально близкие выемочные единицы с одинаковыми параметрами в одну зону. Но даже опытным специалистам будет нелегко проводить группирование при наличии четырёх и более переменных.
Вобщем случае в процедуре кластерного анализа данных используют разные меры сходства, которые можно разделить на следующие типы: меры расстояния (близости или меры удалённости); коэффициенты корреляции (или величина, обратная корреляции); некоторые программные продукты ещё оперируют
скоэффициентами ассоциативности и вероятностными коэффи-
26
циентами сходства. В программных продуктах обычно предполагается, что метрика фиксирована. Вместе с тем выбор метрики во многих случаях не однозначен, поскольку математическая модель сходства объектов может меняться по мере укрупнения кластеров.
Расстоянием (метрикой) между объектами А и B в пространстве переменных именуется такой параметр dab, который удовлетворяет следующим требованиям:
A 1. dab 0, dab 0,
A2. dab dba ,
A3. dab ddc dac .
Другими словами, метрика не может быть отрицательной; величина метрики между первой и второй точкой равна метрике между второй и первой точками; три точки образуют треугольник, сумма двух метрик (линий) треугольника должна быть больше величины третьей метрики.
Мерой близости (сходства) в статистике называется такая величина ab , которая имеет некоторый предел и возрастает с
увеличением близости объектов. Она обладает некоторыми свойствами:
B 1. ab непрерывна,
В2. ab ba ,
В3. 1 ab 0 .
Для перехода от дистанции к мерам близости можно рекомендовать следующее выражение:
|
1 |
. |
(2.3) |
|
|||
|
1 d |
|
|
2.3. Характеристики близости объектов
Ранее отмечалось, что кластеризация процесса формирования компактных множеств может использовать меры близости, например, расстояние между объектами, или меры разли-
27
чия. Расстояния могут определяться как в одномерном, так и многомерном пространстве переменных [73].
Когда мы группируем пункты геодезических или маркшейдерских сетей в двухили трёхмерном пространстве, эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Причём для объединения объектов нет различия в том, являются ли рассчитанные разности (а точнее, суммы квадратов разностей, извлечённые из-под корня) расстояниями между пунктами, или некоторыми разностями в содержании химических, биологических или иных компонентов.
Вкластерном анализе используются произвольные меры расстояния, что более значимо для исследователя. Задачей исследователя является подбор правильного метода для его данных [11; 12].
Внаиболее распространённом программном продукте для статистического анализа данных Statistica используются такие меры сходства объектов: евклидова метрика, квадрат евклидовой метрики, манхэттенское расстояние, или «расстояние городских кварталов», метрика Чебышева, преобразованный коэффициент корреляции Пирсона (1 – коэффициент корреляции), коэффициент совстречаемости (точнее, 1 – коэффициент совстречаемости).
Ранее отмечалось, расстояние между объектами – одна из мер сходства. Интуитивно понятно, что чем меньше расстояние между объектами, тем они более схожи друг с другом. В силу своей простоты меры расстояния (метрики) в расчётах используются очень широко. Два объекта будут одинаковы, если описывающие их переменные принимают одинаковые значения.
Вэтом случае расстояние между ними равно нулю, а чем больше это расстояние, тем меньше становится связь объектов друг с другом. Меры расстояния зависят от выбора шкалы (масштаба) измерений и обычно не ограничены сверху. Одним из наиболее известных расстояний является уже описанное евклидово расстояние, для р-мерного случая определяемое как [25; 46; 73;80]:
28

p |
|
dij = wi (xik x jk )2 , |
(2.4) |
k 1 |
|
где dij – расстояние между объектами i и j; xik – значение k-й переменной для i-го объекта; wi – вес признака.
Такое выражение позволяет использовать более тонкие методы для настройки весов wi отдельно для каждой переменной, приписать «вес», пропорциональный степени важности данной переменной в анализе. Цель «взвешивания» признака состоит в том, чтобы обеспечить максимальную дискриминирующую (разделяющую) способность признака для разделения на кластеры. Величину веса могут назначать эксперты. В примерах с избыточным количеством переменных некоторая часть весов может и обнуляться.
Для придания больших весов более отдаленным друг от друга объектам используют квадрат евклидова расстояния, тогда не надо извлекать квадратный корень.
Если необходимо прогрессивно увеличить или уменьшить вес переменных, относящийся к пространству объектов, используют степенное расстояние. Степенное расстояние вычисляется по формуле
p |
|
|
dij = r (xik |
xjk )n , |
(2.5) |
k 1 |
|
|
где r и p – параметры, определяемые пользователем.
Величина p изменяет взвешивание разностей по отдельным переменным, а значение степени r изменяет меру взвешивания больших расстояний между объектами. Когда оба параметра r и p, равны двум, это расстояние совпадает с расстоянием Евклида.
Вместе с тем использование высоких значений r и p уменьшает информативность некоторых признаков в многомерных пространствах. Чем больше р, тем выше размерность пространства, тем более устойчивой становится сумма разностей.
29
А значит, что все точки пространства становятся почти одинаково удалены друг от друга. Становится затруднительно установить локальную окрестность объекта, теряется информация о структуре метрического пространства.
Расстояние Чебышева равно максимальной разности между значениями соответствующих признаков последовательных пар переменных. Метрику используют тогда, когда требуется определить различие двух объектов по какой-либо одной координате:
dij = max | хi – хj|.
Например, абсолютная разность значений первой переменной равна 2, а второй переменной – 8. Расстояние Чебышева равно большему значению – 8. Расстояние Чебышева является довольно грубой мерой различия, так как значительная часть имеющейся информации игнорируется.
Если не возводить в квадрат покоординатные расстояния, а просто просуммировать их абсолютные значения, получим так называемое манхэттенское расстояние, или «расстояние городских кварталов». Такое расстояние уподобляется перемещению автомобиля по улицам города, в нём существуют определенные правила. Автомобиль может перемещаться только по улицам, нельзя пересечь квартал по диагонали. Такую метрику ещё именуют «расстоянием городских кварталов» (city-block), оно определяется суммой абсолютных разностей пар значений.
Для двумерного пространства это не прямолинейное евклидово расстояние между двумя точками, а путь, который должен преодолеть автомобилист, чтобы проехать от одной точки к другой по улицам, которые пересекаются под прямым углом.
|
|
p |
|
x jk |
r t /r |
(2.6) |
dij |
|
|
xik |
. |
||
|
k 1 |
|
|
|
|
|
30
