
книги / Равновесие анизотропных полых сферических и цилиндрических тел под действием массовых сил
..pdfЗдесь |
|
|
x1 = −1, |
x2 = |
|
A22 |
+ A23 |
+ 2A44 |
, |
|
(1.20) |
||
|
|
|
A12 − A22 − A23 − A44 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
= |
A |
A − 2 |
( A + A ) − 3A + 2( A + A |
)t |
|||||||
|
44 |
12 |
22 |
|
23 |
44 |
12 |
|
44 |
, |
|||
|
3 |
|
|
2( A + A )2 |
− A |
( A + A + 2A |
) |
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
12 |
44 |
|
11 |
22 |
23 |
44 |
|
|
|
|
x |
= |
A |
A − 2 |
( A + A ) − 3A − 2( A + A |
)t |
|||||||
|
44 |
12 |
22 |
|
23 |
44 |
12 |
|
44 |
, |
|||
|
4 |
|
|
2( A + A )2 |
− A |
( A + A + 2A |
) |
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
12 |
44 |
|
11 |
22 |
23 |
44 |
|
|
|
а C1 |
, C2 |
, C3 |
и C4 – постоянные интегрирования, определяе- |
||||||||||
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
мые из граничных условий для n = 1 .
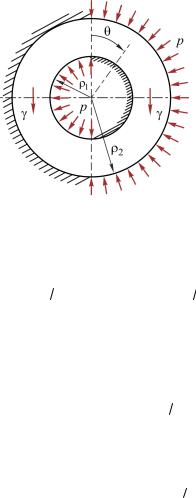
В частном случае для изотропного материала ( t = 5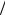 2 ) ко-
2 ) ко-
эффициенты (1.17) и (1.20), содержащиеся в решении (1.19) системы дифференциальных уравнений (1.9) при n = 1 , могут быть записаны в следующем виде:
H |
ρ |
= |
γ(1− ν) |
, H |
θ |
= − |
2γν , x = |
4(1− ν) |
|
, x = |
4ν− 1 |
|
, |
|||||||
|
|
3E |
|
|
|
|
3E |
2 |
|
4ν− 3 |
3 |
2ν− 3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
x1 = −1, |
x4 = 2. |
|
|
|
|
|||||
При n > 1 все системы (1.9) являются однородными, и их |
||||||||||||||||||||
решения находятся также в виде многочленов: |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
= x j ρλjn , |
|
|
= y j ρλjn . |
|
|
|
||||||
|
|
|
u |
n |
uθ |
|
|
|
||||||||||||
|
|
|
|
|
|
j=1 |
n |
|
|
|
n |
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|||
Характеристические |
числа |
|
|
λj |
и коэффициенты |
x j |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
( j = 1,2,3,4 ) для любого n могут быть найдены из решения системы уравнений [33, 37]:
|
λ |
n |
(λ |
n |
+ 1) + β |
3n |
|
λ |
n |
(λ |
n |
+ 1) + α |
= (α |
4n |
λ |
n |
+ α |
5n |
)(β |
4n |
λ |
n |
+ β |
5n |
), |
|||||
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
λj |
|
(λj |
|
+ 1− α4n )+ β3n − α5n |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x jn = |
n |
n |
|
|
, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
λj |
(λj |
+ 1− β4n )+ α3n − β5n |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21

где αsn = asn |
|
a1n и βsn = bsn |
|
b1n . Тогда общее решение систе- |
|||||||||||||||||
мы (1.9) запишем в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u = x C ρλ1n |
+ x C |
2 |
|
ρλ2n + x C ρλ3n + x C |
4 |
|
ρλ4n |
, |
|||||||||||||
ρ |
n |
1 |
|
1 |
2 |
n |
n |
|
3 |
3 |
|
|
|
4 |
n |
n |
|
|
|
||
|
n |
n |
|
|
|
n |
n |
|
|
|
|
|
|
|
|
||||||
|
u = C ρλ1n + C |
2 |
|
ρλ2n + C ρλ3n |
+ C |
4 |
ρλ4n . |
|
|
|
|||||||||||
|
|
θ |
n |
1 |
|
|
n |
|
3 |
|
|
|
n |
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
Постоянные интегрирования |
C1 |
, |
C2 |
, |
C3 |
и |
C4 |
n |
для |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
|
каждого n определяются из граничных условий соответствующей краевой задачи. Заметим, что для n > 1 системы дифференциальных уравнений (1.9) однородны. Это означает, что если разложенные в ряды по θ граничные условия для n > 1 также однородны, то их решения будут тривиальными: uρn = 0 и uθn = 0.
1.2. РАВНОВЕСИЕ ТЯЖЕЛОЙ УПРУГОЙ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОЙ СФЕРЫ С ЖЕСТКО ЗАКРЕПЛЕННОЙ ВНЕШНЕЙ ПОВЕРХНОСТЬЮ, НАХОДЯЩЕЙСЯ ПОД ДЕЙСТВИЕМ РАВНОМЕРНОГО ВНУТРЕННЕГО ДАВЛЕНИЯ
Рассмотрим задачу о равновесии толстостенной транс- версально-изотропной сферы (имеющей внутренний радиус ρ1 и внешний – ρ2 , ρ1 < ρ2 ), находящейся под действием массо-
вых сил и внутреннего давления p, с жестко закрепленной внешней поверхностью (правая часть сферы на рис. 1.1).
Поскольку граничные условия
uρ |
ρ=ρ |
2 |
= 0 , uθ |
|
ρ=ρ2 |
= 0 , τρθ |
ρ=ρ |
= 0 , σρρ |
ρ=ρ = − p (1.21) |
|
|||||||||
|
|
|
|
|
1 |
1 |
|||
не нарушают осевой симметрии задачи, то ее решение может быть получено с помощью метода, изложенного в параграфе 1.1.
22
Разложив граничные условия (1.21) в ряды по меридиональной координате, можем определить постоянные интегрирования, входящие в решения систем дифференциальных уравнений (1.9), для всех членов ряда.
Рис. 1.1. Тяжелая трансверсально-изотропная сфера
Константы интегрирования в уравнениях (1.11) для n = 0 записываются следующим образом:
|
C |
|
= 2 |
p |
ρ3 2+k ρ2k , |
C |
|
|
= −2 |
p |
ρ3 2+k , |
|
(1.22) |
||
|
|
|
2 |
|
|
|
|||||||||
|
1 |
|
|
1 |
2 |
|
0 |
|
|
|
1 |
|
|
||
|
|
0 |
|
K |
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
K = A |
(2k − 1) + 4A |
ρ2k + A |
|
(2k + 1) − 4A ρ2k , |
|||||||||||
|
11 |
|
|
|
12 |
1 |
|
11 |
|
|
12 |
|
2 |
||
входящие в (1.19) постоянные при n = 1 определяются из решения системы четырех линейных алгебраических уравнений [33]:
2C |
|
2A |
(x + 1) − A x ρ1 2+t + |
|
|
||||||||
|
|
21 |
|
12 |
|
2 |
11 |
2 1 |
|
|
|
|
|
+C |
|
4A |
(x + 1) + A x |
( |
2t − 1) ρ1+2t |
+ |
|||||||
31 |
|
12 |
|
3 |
|
11 3 |
|
|
1 |
|
|
||
+C |
41 |
4A |
|
(x + 1) − A x |
(2t + 1) |
ρ = |
|||||||
|
|
12 |
|
4 |
11 |
4 |
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
7 2+t |
, |
|
|
= −4 Hρ ( A11 |
+ A12 ) + Hθ A12 |
ρ1 |
|
|
|||||||||
−C11 + x2C21ρ−21 + x3C31ρ−21 2+t + x4C41ρ−21
2+t + x4C41ρ−21 2−t = −Hρρ22 ,
2−t = −Hρρ22 ,
23

C11 + C21ρ−21 + C31ρ−21 2+t + C41ρ−21
2+t + C41ρ−21 2−t = −Hθρ22 ,
2−t = −Hθρ22 ,
2C21 (x2 + 2)ρ11 2+t + C31 (2x3 − 2t + 3)ρ11+2t + +C41 (2x4 + 2t + 3)ρ1 = 2(Hθ − Hρ )ρ17
2+t + C31 (2x3 − 2t + 3)ρ11+2t + +C41 (2x4 + 2t + 3)ρ1 = 2(Hθ − Hρ )ρ17 2+t .
2+t .
Наиболее простые по структуре постоянные интегрирования имеют вид:
|
KCC4 = 2ρ1tρt2 |
(Hθ {2A12 |
2(3+ 2x2 )(1+ x3 )ρ13ρ122+t − |
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− (5+ 4x |
− 2t)(1+ x |
)ρ7 2+t |
−Y |
ρ1 |
2+t ρ3 |
− |
|
|
(1.23) |
|||
|
|
3 |
|
2 |
1 |
4 |
1 |
2 |
|
|
|
}+ |
|
|
− A11 |
2x2 (1+ x3 )ρ13ρ122+t + (1+ x2 )(2t −1) x3ρ17 2+t + Y2ρ11 2+t ρ32 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ Hρ { |
|
3 1 2+t |
|
|
|
|
7 2+t |
|
1 2+t 3 |
|
+ |
|||
2A12 2(1+ x3 )ρ1ρ2 |
+ (1+ x2 )(2t −1)ρ1 |
|
− Y4ρ1 |
ρ2 |
|
|||||||||
+A11 2(4 + 3x2 )(1+ x3 )ρ13ρ122+t −
−(1+ x2 )(6 + 5x3 − 2t{2 + x3})ρ17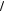 2+t − Y2ρ11
2+t − Y2ρ11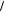 2+tρ32 } ,
2+tρ32 } ,
KCC21 = ρ1ρ122 (−Hρ {4A12ρ2 (1+ x4 )(2t −1)ρ15 2+2t +
2+2t +
+(1+ x3 )(2t +1)ρ15 2ρ22t + (x4 − x3 − 2{2+ x4 + x3})ρ1tρ52
2ρ22t + (x4 − x3 − 2{2+ x4 + x3})ρ1tρ52 2+t +
2+t +
+A11 2(1+ x3 )(6+ 5x4 + 2t{2+ x4})ρ15 2ρ12+2t −
2ρ12+2t −
−2(1+ x4 )(6+ 5x3 − 2t{2+ x3})ρ15 2+2tρ2 −Y5ρ1tρ72
2+2tρ2 −Y5ρ1tρ72 2+t }+
2+t }+
+Hθ {4A12 (1+ x4 )(5+ 4x3 − 2t)ρ15 2+2tρ2 − (1+ x3 )(5+ 4x4 + 2t)ρ15
2+2tρ2 − (1+ x3 )(5+ 4x4 + 2t)ρ15 2ρ12+2t + + (x3 − x4 + 2{2+ x4 + x3})ρ1tρ72
2ρ12+2t + + (x3 − x4 + 2{2+ x4 + x3})ρ1tρ72 2+t + A11ρ2 2x3 (1+ x4 )(2t −1)ρ15
2+t + A11ρ2 2x3 (1+ x4 )(2t −1)ρ15 2+2t + +2x4 (1+ x3 )(2t +1)ρ15
2+2t + +2x4 (1+ x3 )(2t +1)ρ15 2ρ22t +Y5ρ1tρ52
2ρ22t +Y5ρ1tρ52 2+t }),
2+t }),
24

KC = A11 {2 Y1 (1+ x3 )ρ22t + Y2 (1+ x4 )ρ12t ρ11 2ρ12 2 − Y5 [1+ x2 ]ρ11+t ρt2} +
2ρ12 2 − Y5 [1+ x2 ]ρ11+t ρt2} +
|
|
|
2t |
|
|
2t |
1 2 |
1 2 |
− |
|
|
+4A12 { Y3 |
(1+ x3 )ρ2 |
+ Y4 (1+ x4 )ρ1 |
ρ1 |
ρ2 |
|
||||||
−[1+ x |
] (1+ x |
)(2t − 1) |
+ (1+ x |
)(2t + 1) |
ρ1+t ρt |
. |
|||||
2 |
|
4 |
|
|
3 |
|
|
|
1 |
2} |
|
Здесь |
|
|
|
|
|
|
|
|
|
|
|
Y = 2x |
[2t + 1]− x |
3 + x + 2t (1− x ) |
, |
|
|
||||||
1 |
4 |
|
2 |
|
4 |
|
4 |
|
|
|
|
Y3 = (1+ x2 )(2t + 1) − 2(1+ x4 ), Y4 = (1+ x2 )(2t − 1) + 2(1+ x3 ),
Y = 2x |
[2t − 1]+ x |
3 + x + 2t (x − 1) |
, |
||||
2 |
3 |
2 |
|
3 |
3 |
|
|
Y5 = x4 (3 − 4t [t − 1]) + x3 (4t[1+ t + 2x4 ]− 3).
Остальныепостоянныенеприводятсяввидуихгромоздкости. Обратим внимание на то, что для n >1 решения систем диф-
ференциальных уравнений (1.9) тривиальны ( uρn = 0 и uθn = 0 )
всилу однородности граничных условий, а коэффициенты (1.17), (1.18) и (1.20), входящие в (1.23), определяются деформационными характеристиками материаласферы.
Решение задачи о равновесии толстостенной тяжелой изотропной сферы, находящейся под действием внутреннего давления p, с жестко закрепленной внешней поверхностью может быть записано как частный случай полученных соотношений [33, 39]. Для этого следует провести замену (1.13) деформационных постоянных в выражениях (1.4).
Тогда решение системы дифференциальных уравнений (1.7) можнопредставитьввиде:
|
C2 |
|
|
|
|
|
C2 |
|
|
|
|
|
2 |
|
C4 |
|
|
|
2 |
|
|
||
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||
uρ = C1 ρ + |
|
|
+ |
x2 |
|
|
|
− C1 |
+ x3C3 ρ |
+ 2 |
|
|
ρ + Hρρ |
cos θ , (1.24) |
|||||||||
ρ2 |
|
|
ρ |
|
|
ρ3 |
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= |
|
|
|
+ |
C2 |
+ C ρ2 |
+ |
C4 |
|
+ H |
ρ2 |
|
|
|
θ , |
|||
|
|
u |
θ |
C |
|
1 |
1 |
|
|
sin |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
ρ |
3 |
|
|
ρ3 |
|
|
θ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
25

H |
ρ |
= |
γ (1− ν) |
, H |
θ |
= − 2γν |
, |
x = |
4(1− ν ) |
, |
x = |
4ν − 1 |
|
, |
|
|
3E |
|
3E |
|
2 |
4ν − 3 |
|
3 |
2ν − 3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
определяя из (1.22) и (1.23) константы интегрирования следующим образом:
|
3 |
|
|
|
|
3 |
3 |
|
|
|
1− ν − 2ν2 |
|
|
||||||
C10 = − pρ1 K |
, C20 = pρ1ρ2K , K = |
|
|
|
, |
||||||||||||||
E 2 |
(1− 2ν )ρ3 + (1+ ν )ρ3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
γ (ν + 1) |
8 |
|
2 |
|
|
8 |
|
2 |
|
|
|
|
||||
C11 = |
|
2ρ1 (6ν |
|
+ ν − 5)− 18ρ2 |
(2ν |
|
− 3ν + 1)+ |
|
|
||||||||||
3NMR |
|
|
|
|
|||||||||||||||
|
|
+ρ15ρ32 (6ν2 + ν − 2)− 9ρ13ρ52 (8ν2 − 12ν + 5) , |
(1.25) |
||||||||||||||||
|
|
|
|
|
|||||||||||||||
C31 |
= |
γ (2ν − 3) |
ρ15 (ν2 + ν )− 2ρ52 (3ν2 − 4ν + 1)− ρ13ρ22 (1+ ν ) , |
||||||||||||||||
|
|||||||||||||||||||
|
|
|
NM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
= γρ5ρ2 |
1+ ν |
|
2ρ3 (1− 2ν ) + ρ3 |
(1+ ν ) |
, |
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
41 |
|
|
1 2 |
3NM |
2 |
|
1 |
|
|
|
|
||||
C21 = − Nγ ρ13 (4ν2 + ν − 3) ,
N= 6E(ν −1) , M = 2(2 − 3ν )ρ52 + (1+ ν )ρ15 .
Вслучае отсутствия внутреннего давления решение (1.24) системы (1.7) для изотропной сферы несколько упрощается. Так
как |
граничные |
условия |
при |
n = 0 |
однородные |
( p = 0 ), то |
|
uρ |
= 0 . Следовательно, |
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
uρ = uρ |
cosθ , |
uθ |
= uθ sin θ. |
(1.26) |
|
|
|
1 |
|
|
1 |
|
Здесь uρ |
и uθ |
определяются выражениями (1.19) с коэффици- |
|||||
|
1 |
1 |
|
|
|
|
|
ентами (1.25). Этот частный случай совпадает с решением, полученным авторами [44, 51]. Заметим, что если сфера изготовлена из изотропного материала, то уравнения (1.16) для нахождения Hρ и Hθ упрощаются и примут одинаковый вид. Тогда
26

из двух одинаковых уравнений можно определить только связь между этими коэффициентами, что и было сделано авторами [44, 51]. Однако, если подстановку деформационных постоянных (1.13) производить в уравнения (1.17), учитывающие ограничения на материальные константы трансверсально-изотроп- ного материала, можно определить явный вид этих коэффициентов: Hρ = γ (1− ν)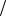 (3E) и Hθ = − 2γν
(3E) и Hθ = − 2γν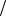 (3E) , что принципиально
(3E) , что принципиально
нельзя было сделать ранее.
В другом частном случае, когда при определении напря- женно-деформированного состояния можно пренебречь вкладом массовых сил, из полученных уравнений следует классическое аналитическое решение задачи Ламе для трансверсально-изот- ропной сферы [56, 113]. Из этого решения для закрепленной по внешней поверхности трансверсально-изотропной сферы со свободной от нагрузок внутренней границей следует тривиальный результат: рассматриваемое тело находится в ненапряженном состоянии.
Подстановка (1.11) и (1.19) с учетом (1.12), (1.17), (1.18), (1.20), (1.22) и (1.23) последовательно в геометрические (1.5) и определяющие (1.3) соотношения позволяет записать выражения для компонент тензора напряжений:
σ |
ρρ |
= 1 |
ρ−3 2−k |
{C |
|
|
[4A − A |
|
|
(1 |
+ 2k )] + C |
2 |
[4A − A |
(1− 2k )]ρ2k } + |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
12 |
|
|
|
11 |
|
|
|
|
|
|
12 |
|
11 |
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
+ x |
|
) |
C2 |
|
+ |
(1+ x |
|
)C |
|
ρ−3 2+t + (1+ x |
)C |
|
ρ−3 2−t + |
|||||||||||||||
+ |
|
2A |
|
|
|
|
1 |
|
|
4 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
12 |
|
|
2 |
|
|
ρ2 |
|
|
|
|
3 |
|
|
|
3 |
|
|
|
4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
(1.27) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|||||
+ (H |
|
+ H |
|
)ρ |
− 1 A |
|
|
|
+ (1− 2t ) x C |
|
ρ−3 2+t |
+ |
|
|||||||||||||||||||||||
ρ |
θ |
|
2x |
2 |
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
11 |
|
|
ρ |
2 |
|
|
|
3 31 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ (1+ 2t ) x C |
41 |
ρ−3 2−t − 4H |
ρ |
ρ cosθ, |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
27

σϕϕ = σθθ = 12 ρ−3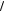 2−k {C10 [2( A22 + A23 ) − A12 (1+ 2k )] +
2−k {C10 [2( A22 + A23 ) − A12 (1+ 2k )] +
|
|
|
|
+C2 [2 |
( A22 + A23 ) − A12 (1− 2k )]ρ2k }+ ( A22 + A23 )× |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
(1 |
+ x |
) |
|
C2 |
+ (1 |
+ x )C |
|
ρ−3 2+t |
+ (1 |
+ x |
|
)C |
|
ρ−3 2t |
+ (H |
|
+ H |
|
)ρ |
|
− |
||||||||
|
|
|
1 |
|
|
|
|
ρ |
θ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
3 |
3 |
|
|
|
|
4 |
4 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
C2 |
|
|
|
|
|
−3 2+t |
|
|
|
|
|
−3 2−t |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
− |
|
|
A12 2x2 |
|
|
|
|
+ |
(1− 2t) x3C3 ρ |
|
|
+ (1+ 2t) x4C4 |
ρ |
|
− 4Hρρ cosθ, |
||||||||||||||||
2 |
|
ρ2 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
τρθ = − A44 ( |
2 + x2 ) |
C21 |
+ (3 + x3 − t )C31ρ−3 2+t + |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ (3 + x4 + t )C41ρ−3 2−t |
|
+ (Hρ |
− Hθ )ρ sin θ . |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если в качестве примера предположить, что железобетонные монолитные крепи сферических подземных выработок или хранилищ в массиве горных пород, которые используются для длительного хранения высокоагрессивных и реакционно-способ- ных твердых и жидких сред, представляют собой толстостенные сферические тела, жестко закрепленные по внешней поверхности, то на основе полученных соотношений можно проанализировать вклад массовых сил в напряженное состояние, а также провести оценку начальной прочности по совокупности критериев, описывающих различные механизмы разрушения.
Железобетон и горные породы содержат в своей структуре стержневые армирующие элементы, объединенные в каркас, и минеральные частицы. Поэтому эти материалы проявляют ярко выраженную анизотропию прочностных и деформационных свойств. Прочностной анализ элементов конструкций и сооружений, изготовленных из железобетона, находящихся в массиве горных или осадочных пород, необходимо осущест-
28

влять на основе многокритериального подхода [18], рассматривая различные механизмы частичного или полного исчерпания несущей способности, характерные для анизотропных повреждаемых сред.
На основе введенных в работах [77, 85–87] независимых величин:
JσI = 1 |
( σϕϕ + σθθ ), |
JσII = σρρ , |
2 |
|
|
JσIII = ( σϕϕ − σθθ )2 + 4τϕθ2 , |
JσIV = τϕρ2 + τθρ2 , |
|
инвариантных относительно ортогональных преобразований, допустимых над сферически трансверсально-изотропным однородным телом.
Сравнение независимых инвариантов тензора напряжений со своими критическими значениями, определяемыми экспериментально, может позволить провести оценку возможности реализации следующих механизмов частичного повреждения: от растяжения или сжатия в меридиональном и радиальном на-
правлении (описывается JσI и JσII ), от сдвига по сферическим поверхностям изотропии и межслоевого сдвига (описываются JσIII и JσIV ). Полная потеря несущей способности будет иметь
место, если будет выполнена вся совокупность критериальных условий в виде неравенств.
На рис. 1.2 представлены распределения независимых инвариантов тензора напряжений в монолитной железобетонной крепи вдоль меридиональной и обезразмеренной радиальной ρ = (ρ − ρ1 )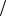 (ρ2 − ρ1 ) координаты [33, 39]. Параметры геомет-
(ρ2 − ρ1 ) координаты [33, 39]. Параметры геомет-
рии и постоянные для особо тяжелого железобетона были вы-
браны |
следующими: |
ρ1 = 3,0 м, ρ2 = 6,0 м; E = 50,0 ГПа, |
E = 35,0 |
ГПа, G = 56,5 |
ГПа, ν = 0,075 , ν = 0,15 и γ = 40 кН/м3 . |
29
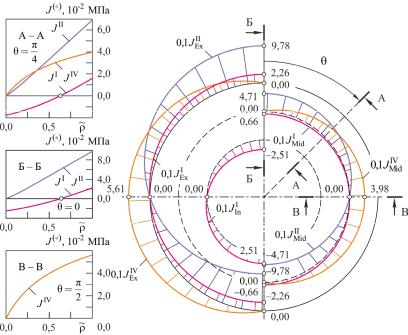
Рис. 1.2. Распределение независимых инвариантов тензора напряжений (КПа) на закрепленной внешней ( JEx( ) ), свободной от нагрузок внутренней ( JIn( ) ) и серединной ( JMid( ) ) поверхностях
Как видим, на внутренней свободной от нагрузок поверхности (р = 0 МПа) монолитной крепи ненулевым является только
первый инвариант JσI , который (за исключением горизонтальной
диаметральной плоскости) в верхней полусфере всюду возрастает вдоль ρ , а в нижней – всюду убывает, принимая нулевое значе-
ние при ρ = 0,63 (см. рис. 1.2). Была обнаружена следующая тре-
бующая дополнительного исследования закономерность: радиальная координата ρ точки, в которой при заданной геометрии
крепи и деформационных свойствах бетона JσI = 0 , постоянна и не зависит от значения меридиональной координаты.
30
