книги / Моделирование электротехнических систем и систем автоматики

ний используют метод понижения порядка дифференциального уравнения, суть которого состоит в том, что производная высокого порядка заменяется другой переменной, производная которой на один порядок понижается.

6.5.6. Решение дифференциальных уравнений высших порядков по методу Рунге–Кутта

Суть метода понижения порядка дифференциального уравнения состоит в том, что производная высокого порядка заменяется любой другой переменной и на основе этой переменной записывается новое дифференциальное уравнение.

Например, для понижения порядка уравнения

произведем в нем замену следующего вида:

после чего исходное уравнение приобретет вид

После такой замены дифференциальное уравнение высокого порядка заменяется системой уравнений первого порядка, при этом число уравнений в системе равно порядку исходного уравнения. Поэтому в нашем примере такая система будет иметь вид

dydt + y = 0,

(51)

dxdt = y.

Таким образом, для уравнений порядка выше двух необходимо будет производить несколько замен переменных. Число

61

этих замен равно степени дифференциального уравнения. Применение метода Рунге–Кутта при моделировании рассмотрим на примере цифровой модели колебательного звена системы автоматики.

6.6. Цифровая математическая модель колебательного звена системы автоматики

Прямая аналоговая модель колебательного звена системы автоматики представлена на рис. 29. В этой модели катушка индуктивности L является элементом способным запасать энергию источника U1, а затем отдавать ее через сопротивление R для зарядки конденсатора С. Заряженный конденсатор, разряжаясь через это сопротивление, вновь способствует накоплению энер-

Таким образом, в этом звене возникает колебательный процесс перетока энергии от элемента L к элементу С и обратно. Математическая модель этого вида динамического звена описывается уравнением

Уравнение этой математической модели может быть решено на ЭВМ в численном варианте. Для этой цели уравнение (52) представим в следующем виде:

62

Для понижения порядка этого уравнения заменим его системой из двух уравнений:

dYdt1 = CL U1 − RL Y1− CL Y ,

(54)

dYdt =Y1.

Решение этой системы дифференциальных уравнений методом Рунге–Кутта получим с помощь программы, записанной на языке Паскаль. Этапы выполнения этой программы представлены ниже:

Приращение аргумента–> x:=x+h/2;

Подпрограммы ППЧ –> f[1]:=C*(u1-y[1])/L-R*y[2]/L; f[2]:=y[1];

for i:=1 to n do begin

Fk4[i]:=h*f[i];

y[i]:=Z[i]+(Fk1[i]+2*Fk2[i]+2*Fk3[i]+Fk4[i])/6; Z[i]:=y[i]; end;

Вывод результата–> {writeln('x=',x,' ','y=',y[1]);}

Конец итерации–> until

Если в вышеописанной программе циклически менять значение параметра R, то полученный результат будет соответствовать графикам, представленным на рис. 30.

Рис. 30. Результат моделирования поведения колебательного звена при дискретном изменении параметра R

Анализ этого результата показывает, что при данных параметрах колебательного звена его колебательный процесс затухает со временем, кроме того, с увеличением значения параметра R снижается амплитуда этих колебаний и возрастает их частота. По аналогии, дискретно меняя другие параметры этой модели, можно установить закономерность их влияния на колебательный процесс.

Таким образом, реализация аналитических моделей всегда требует составления реальных программ для решения уравнений этих моделей. Составление таких программ требует необ-

64

ходимых навыков и определенных затрат времени для их отладки. Эти обстоятельства часто являются серьезным препятствием применения этого метода в практическом моделировании.

7. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Развитие возможностей электронных вычислительных машин и совершенствование их программного обеспечения позволило перевести процесс численного моделирования на принципы имитационного моделирования. Имитационные модели часто относят к моделям анимационного типа, так как наличие

вних анимационных эффектов обеспечивает соизмеримость моделируемых процессов с их оригинальной реальностью.

Реализация возможностей анимации в математических моделях стала реальностью только тогда, когда ЭВМ получила возможность вывода информации в графическом режиме, а это,

всвою очередь, стало возможным только при наличии в структуре ЭВМ достаточных ресурсов ее оперативной памяти в сочетании с необходимым быстродействием обработки цифровой информации.

Принципы машинной графики в сочетании с возможностями мультипликации легли в основу реализации анимационных, имитирующих моделей.

Имитационной моделью называют такую разновидность

математической модели некоторого физического процесса (в том числе электротехнической системы или системы автоматики), результат моделирования которой максимально приближен не только по характеру его проявления, но и по внешнему физическому сходству к оригиналу. Имитационная модель на ЭВМ реализуется через отдельные подпрограммы, объединенные в единый алгоритм. В основу работы имитационных моделей положены принципы анимации, которые предполагают сочетание:

65

•результата решения уравнений математической модели;

•машинной графики;

•мультипликации.

7.1.Принципы анимации в имитационных моделях

В имитационных моделях часто реализуются анимацион-

ные эффекты. Анимационный эффект – это способность мо-

дели не только представлять внешнее сходство моделируемого объекта, но и способность модели отражать его динамические

(или рабочие) качества. Поэтому имитационные модели с анимационными качествами всегда относятся к моделям динамического типа. Анимационные эффекты в имитационных моделях могут быть реализованы как на плоскости (модели типа 2D) так и в трехмерном пространства (модели типа 3D).

Анимационные эффекты в имитационных моделях реализуются через команды машинной графики конкретного алгоритмического языка. В частности, на языке «ПАСКАЛЬ» это может быть сделано с помощью следующих команд:

–команда putpixal (x,y.f) − изображение точки на экране дисплея;

–команды line to (x,y) или line (x1,y1,x2,y2) − изображение линии на экране дисплея;

–команда rectangle (x1,y1,x2,y2) − изображение прямоугольника на экране дисплея;

–команда circle (x,y,r) − изображение окружности на экране дисплея;

–команда arc (x,y,φ0,φi,r) − изображение дуги на экране дисплея;

–команда sector (x,y,φ0,φi) − изображение сектора на экране дисплея.

Рассмотрим принципы программирования анимационных эффектов на следующих примерах.

66

Пример 1. Составить алгоритм для анимационного изображения на плоскости с помощью точек символа (буквы) «П».

Положения точки на поле носителя информации в программном пакете «ПАСКАЛЬ» осуществляется командой putpixal (x,y.f). В этой команде: x,y – координаты точки; f – цвет

символа, команда putpixal (x,y.f) применяется во вложенном цикле. Алгоритм вывода этого символа представлен на рис. 32.

Рис. 32. Структура алгоритма изображения символа «П»

Этот алгоритм состоит из двух вложенных циклов. Внешний цикл этой вложенности открывается по параметру Y с числом повторений, равным 7. Этим циклом контролируется

67

положение точек в символе «П» по вертикали. Внутренний цикл этой вложенности открывается по параметру Х с числом повторений равным 5. Этим циклом контролируется положение точек указанного символа по горизонтали. Принято, что координата (Х=0, Y=0) соответствует точке, расположенной в верхнем левом углу матрицы, поэтому во внутреннем цикле по истинности условия Y=0 командой putpixal (x,y.f) выводятся на печать все точки верхней строки буквенной матрицы. После первого выхода из внутреннего цикла условие Y=0 становится ложным, поэтому проверяется следующее условие (Х=0)OR(Х=4), по которому командой putpixal (x,y.f) точки ставятся только в позиции ноль и четыре во всех остальных строках матрицы.

Пример 2. Составить алгоритм для анимационного изо-

бражения процесса перемещения линии по полю носителя информации (плоскости). Положение линии на носителе информации может быть отображено одной из следующих команд программного пакета «ПАСКАЛЬ»: lineto(x,y) и line(x1,y1,x2,y2). По команде lineto(x,y) линия на поле носителя информации проводится от точки положения на нем курсора до точки с координатами x,y. По команде line(x1,y1,x2,y2) эта линия проводится от точки с координатами x1,y1, до точки с координатами x2,y2. В обоих случаях цвет линии предварительно задается командой setcolor(f), где f – код соответствующей цветовой гаммы.

Рассмотрим варианты использования этой команды в анимационных моделях на следующем примере. Первоначально обеспечим удлинение исходной линии с поворотом ее на 45 градусов.

В этом фрагменте примера командой line(x1,y1,x2,y2) в цикле происходит приращение параметров:

Х2 = Х2 + 1 и Y2 = Y2 + 1, при этом па-

раметры Х1 и Y1 остаются неизменными.

68

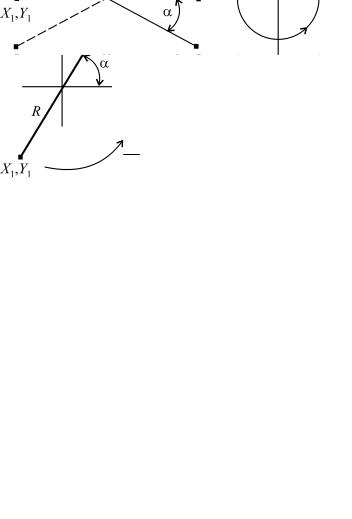
В следующем фрагменте этого примера первоначально повернутая на 45 градусов прямая линия начинает вращаться вокруг своего центра симметрии. При этом радиус поворота» зависит от значения параметров Х2,Y2 и определяется по следующему уравнению:

В результате этого поворота координаты концов прямой

В третьем фрагменте этого примера концы горизонтальной прямой линии совершают круговое движение относительно оси Х. Схема этого фрагмента выглядит следующим образом.

Величина радиуса вращения концов этой прямой заранее задается. Величина этого радиуса, определяет значение параметра Y1, (как проекцию вращающегося конца прямой линии на плоскость). Величина этого параметра зависит от значения угла β поворота вращающегося конца этой линии.

69

В результате поворота концов этой линии на угол β (от 0 до 360°) параметры модели меняются следующим образом:

Все фрагменты этого примера последовательно описываются алгоритмом, представленным на рис. 33.

После запуска этого алгоритма вводятся исходные данные, среди которых координаты исходной прямой (X1, Y1, X2, Y2)

ирадиус прецессии вращения ее торцов R1. Следующим опера-

тором line(x1,y1,x2,y2) изображается исходное положение линии и по формуле (55) производится расчет радиуса ее последующего вращения.

Первым анимационным процессом с этой прямой является процесс трансформации ее длины и изменения углового положения относительно осей координат. Этот процесс осуществляется в цикле. Счетчиком этого цикла является изменяемый па-

раметр Х2, величина которого меняется от 1 до 10. В этом цикле одновременно меняется параметр Y2. В результате этого прямая линия за десять циклов одновременно увеличивается в размере

инаклоняется к оси Х.

Вследующем цикле анимация этой прямой связана с ее вращением, которое происходит в плоскости координат Х, Y относительно точки ее середины (симметрии). Этот поворот осу-

ществляется в диапазоне изменения угла α от 45 до 180°. При этом значение координат (X1, Y1, X2, Y2) этой прямой вычисляется в соответствии с формулами (56).

70