
книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL
.pdfПри нарушении этого условия во многих формулах уменьшение свободы выбора для бесповторной выборки учитывается коэффициентом (1 – n/N).
Понятия повторной и бесповторной выборок не имеют особого смысла для результатов повторяющихся измерений, выполняемых для случайной характеристики одного объекта, т.к. результат каждого измерения нельзя вернуть в генеральную совокупность. Здесь более существенным фактором является регламентация процедуры случайного выбора, например при измерении диаметра шейки коленвала нужно проводить измерения диаметра с различными установками измерительного инструмента по длине шейки и угловой координате конкретного диаметра.
Отобранные объекты могут характеризоваться одним или несколькими признаками (одномерные и многомерные выборки), измеренными в различных шкалах измерений. Шкалы признаков могут быть различными, наиболее распространены порядковые (например, оценка за экзамен), номинальные (например, номер цвета в палитре цветов) и количественные (например, шкалы времени, длины).
Для того чтобы по исследованию выборки можно было сделать выводы о поведении интересующего нас признака генеральной совокупности, нужно, чтобы выборка правильно представляла пропорции генеральной совокупности, то есть была представительной (репрезентативной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если объектов достаточно много и каждый объект выбран случайно, причем для любого объекта вероятность попасть
ввыборку одинакова.
Вконкретных условиях для обеспечения репрезентативности используют различные методы отбора и их комбинации:
–собственно случайный (простой), при котором единицы совокупности или их группы извлекаются по жребию или по
11
таблице случайных чисел, при этом элементы совокупности должны иметь равную вероятность попасть в выборку;
–типический (расслоенный случайный) – генеральную со-
вокупность разбивают на типические группы и отбор внутри группы осуществляют собственно случайным способом;
–механический, при котором осуществляется отбор каждой n-й (например, единицы совокупности; чаще используется для совокупностей, упорядоченных каким-либо образом; при таком отборе велика опасность систематической ошибки);
–серийный – элементы из генеральной совокупности отбираются сериями (партиями, группами), которые должны обследоваться при помощи сплошного обследования.
Измеренные значения изучаемого признака могут содер-
жать грубые ошибки, появляющиеся в результате сбоя измерительных систем, ошибок оператора («человеческий фактор») и тому подобных причин. Формальная статистическая обработка таких выборок может дать неверные результаты. Поэтому выборки подвергают цензуресцелью выявления подобных ошибок.
Наиболее простым и эффективным приемом выявления грубых ошибок является графическое представление выборочных данных в различных формах, а также сравнение минимального и максимального значений с остальной совокупностью результатов.
Удаление из выборки сильно отклоняющихся от среднего значения минимальных или максимальных значений (цензури-
рование выборки слева или справа) выполняется на основе де-
тального анализа возможных причин таких отклонений и/или с помощью различных статистических критериев, сводящих к минимуму риск удаления действительно наблюдаемых значений.
Неаргументированное удаление из выборок значений, не нравящихся исследователю по каким-то субъективным причинам, чаще всего является подгонкой результатов и осуждается с этических позиций.
12
1.2. Основные распределения случайных величин, используемые в математической статистике
Математическая статистика использует распределения вероятности для специальных случайных величин (статистик), вычисляемых по выборке. Чаще всего применяются распределения: стандартное нормальное, χ2 , Стьюдента и Фишера (Фи-
шера – Снедекора).
Их отличительной особенностью является следующее обстоятельство: стандартный нормальный закон распределения имеет известные параметры, а параметры остальных указанных законов имеют смысл степеней свободы, определяемых через объемы выборок.
Приведем определения и некоторые свойства этих распределений для произвольной случайной величины Х (опуская далее в некоторых случаях для простоты индекс «х» в обозначениях математического ожидания mx, дисперсии
Dx , среднеквадратичного отклонения σx и их точечных оце-
нок m |
, D , D |
,σ |
, |
σ |
, вычисляемых по выборочным |
x |
x x испр |
x |
|
x испр |
|
данным).
При определении границ доверительных интервалов, при нахождении критических точек в процедурах проверки статистических гипотез типичной операцией является вычисление специальной числовой характеристики конкретного распределения вероятностей случайной величины Х с функцией распределения F(x) – квантиля xр. Для заданного уровня вероятности р квантиль xр является решением уравнения Р{X< xp} = F(xp) = p.
На числовой оси возможных значений случайной величины Х точка xр определяет границу левосторонней области, в которую с вероятностью р попадут случайные точки Х. Вероятность противоположного события – случайные точки Х попадут правее xр, определяется выражением Р{X ≥ xp} = 1 – p.
13
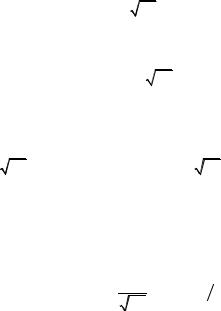
Графический способ решения этого уравнения показан на рис. 1.1: на оси ординат графика F(x) откладывается заданное значение р, от этого значения идем вправо по горизонтальной штриховой линии до пересечения с кривой F(x), из точки пересечения спускаемся по вертикали вниз до пересечения в точке
xр с осью х.
На практике для определения xр используют справочные таблицы типа таблиц приложений [2] или численные процедуры современных статистических программ, например обратные статистические функции MS Excel.
1.2.1. Стандартное нормальное распределение N (0; 1)
Стандартное нормальное распределение N (0; 1) является частным случаем (а = 0; σ2 = 1) нормального распределения N (а; σ2), имеющего функцию плотности распределения
|
1 |
|
(x − a)2 |
|
||
f (x) = |
|
exp − |
|
|
|
(1.1) |
σ 2π |
2σ |
2 |
||||
|
|
|
|
|
||
и функцию распределения
x |
|
1 |
x |
|
(t − a)2 |
|
|
||
F(x) = ∫ f (t) dt = |
|
|
∫ exp |
− |
|
|
|
dt. |
(1.2) |
σ |
|
2σ |
2 |
||||||
−∞ |
2π −∞ |
|
|
|
|
|
|||
Дифференциальная и интегральная функции распределения N (0; 1) имеют следующий вид (см. рис. 1.1):
f (х) = |
1 |
|
− |
x2 |
|
; F(х) = Ф(x) = |
|
|
exp |
|
|
||||
2π |
2 |
||||||
|
|
|
|
|
1 х |
|
− |
t2 |
|
|||
|
|
exp |
|
dt. |
(1.3) |
||
2π −∞∫ |
2 |
||||||
|
|
|
|
||||
Функцией распределения случайной величины X~N (0; 1) является функция Лапласа Ф(х), причем в справочных табли-
цах чаще всего для x ≥ 0 приведена нормированная функция Лапласа Ф0 (х) :
х |
|
Ф0 (х) = 12π ∫0 exp (−t2 2) dt, |
(1.4) |
14
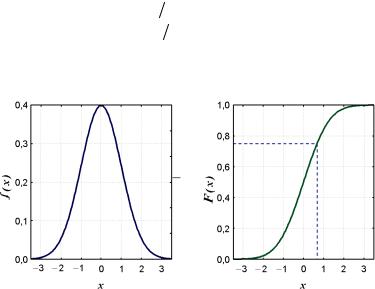
при этом связь функции Лапласа с нормированной функцией Лапласа имеет вид
|
0 |
(−х) , x < 0 ; |
|
1 2 −Ф |
(1.5) |
||
Ф(х) = |
1 2 +Ф0 (х) , x ≥ 0 . |
||
|
|
||
Математическое ожидание и дисперсия распределения N (0; 1) равны соответственно 0 и 1.
|
а |
б |
|
Рис. 1.1. Дифференциальная (а) и интегральная (б) функции |
|||
|
|
распределения для N (0; 1) |
|
Для практического применения таблиц Ф0 (х) |
при вычис- |
||
лении |
нужных |
квантилей заданного уровня |
вероятности |
up ≡ xp |
(для обозначения квантиля стандартного нормального |
||
распределения xp |
используется специальное обозначение up ) |
||
в качестве уравнения F( up ) = p нужно использовать его представление через функцию Ф0 (х), а также учитывать свойства симметрии этого распределения: u 1−p = −up . Для перехода от
(1.1)–(1.2) к (1.3)–(1.4) – нормированию и центрированию случайной величины Х, делают замену переменных: z = (x −a) / σ.
15
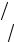
Уравнение для нахождения квантиля up через функцию Ф0 (х) имеет вид
|
1 2 −Ф |
0 |
(−u |
p |
) , p <1/ 2; −u |
p |
< 0 ; |
|
|||
|
|
|
|
|
|
|
|
(1.6) |
|||
|
p = |
1 2 +Ф0 (up ) , |
p ≥ |
1/ 2; up ≥ 0 . |
|||||||
|
|
|
|||||||||
|
Например: |
|
|
|
|
|
|
|
|
|
|
u0,2 |
= −0,8416 = −u1−0,2 = −u0,8 |
Ф0 (−u0,2 ) = 0,5 −0,2 = 0,3; |
|||||||||
u0,8 |
= 0,8416 Ф0 (u0,8 ) = 0,8 −0,5 |
= 0,3. |
|
|
|
||||||
При оценке доверительных интервалов и проверке статистических гипотез с двусторонней критической областью для заданной доверительной вероятности (надежности) β =1−α воз-
никает необходимость |
вычисления квантилей |
uα/ 2 = –u1−α/ 2 |
( u(1−β)/ 2 = – u(1+β)/ 2 ), |
определяющих границы |
соответствую- |
щих доверительных интервалов и критических областей. Ис-
пользуя нормированную функцию Лапласа |
Ф0 (х) |
[2] для |
||
α/ 2 < 0,5, можно вычислить квантиль u1−α/ 2 |
как |
решение |
||
уравнения |
|
|
|
|
Ф0 (u1−α/ 2 ) = Ф0 (u(1+β)/ 2 ) = |
1−α |
= |
β |
|
|
2 . |
(1.7) |
||
2 |
||||
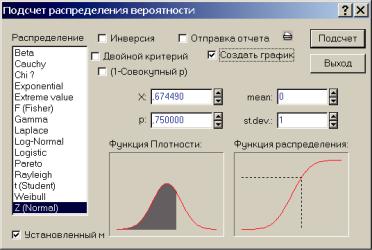
При использовании современных математических пакетов для персональных компьютеров нет нужды пользоваться многочисленными справочными таблицами для различных законов распределения. Например, рис. 1.1 получен с помощью вероятностного калькулятора пакета STATISTICA 6.0, диалоговое окно которого показано на рис. 1.2.
Задача вычисления квантиля уровня р = 0,75 для стандартного нормального распределения здесь сводится к выбору нужного закона распределения Z(Normal), заданию числовых значений его параметров (a = mean = 0; σ = st.dev. = 1), заданию
16
PNRPU
значения 0,75 в соответствующем окне. Результат u0,75 ≡ x0,75 =
= 0,674490 в числовой и графической форме отображается в окне «X» и на графиках обеих функций распределения.
Рис. 1.2. Меню вероятностного калькулятора пакета STATISTICA 6.0
В табличном процессоре Excel 2003 для работы с нормальным распределением можно использовать следующие встроенные статистические функции (см. прил. 2):
–НОРМСТРАСП (х) – возвращает (вычисляет) F(x) для стандартного нормального распределенияN (0; 1);
–НОРМРАСП (х; а; σ; ИСТИНА) – возвращает F(x) для нормального распределенияN (а; σ2);
–НОРМРАСП (х; а; σ; ЛОЖЬ) – возвращает f(x) для нормальногораспределенияN (а; σ2);
–НОРМСТОБР (р) – возвращает квантиль uр = xр для стандартного нормального распределенияN (0; 1);
–НОРМОБР (р; а; σ) – возвращает квантиль xр для нормальногораспределенияN (а; σ2).
Пример 1.1. Вычислить с помощью функции НОРМСТРАСП (х)
вMS Excel функцию распределения F(x) стандартного нормального распределенияN (0; 1) длязначенийх: –3, –2, –1, 0, 1, 2, 3.
17
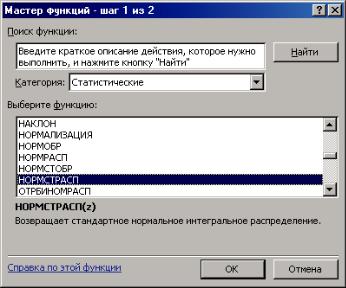
Решение: Зададим в ячейках A1, B1 названия столбцов: х и F(x), в А2:А8 – значения аргумента х, в ячейке В2 – функцию НОРМСТРАСП(A2):
–щелчком левой клавиши мыши (далее – ЛКМ) по ячейке В2 делаем ее активной;
–затем щелчком ЛКМ по кнопке ввода функций fx попа-
даем в окно «Мастера функций», где в категории «Статистические» находим нужную функцию (рис. 1.3);
Рис. 1.3. Меню мастера функций MS Excel
– двойным щелчком ЛКМ по названию выбранной функции вызываем окно задания ее аргументов (рис. 1.4), где в поле для задания единственного аргумента этой функции указываем ячейку А2 (все адреса ячеек в Excel набираются латинскими буквами, а имена функций – русскими, ошибка возникает даже при совпадении символов, например, АRU ≠ AEN, поэтому желательно пользоваться «Мастером функций»), <ОК>, в результате имеем результат для х = –3 (рис. 1.5, а);
18
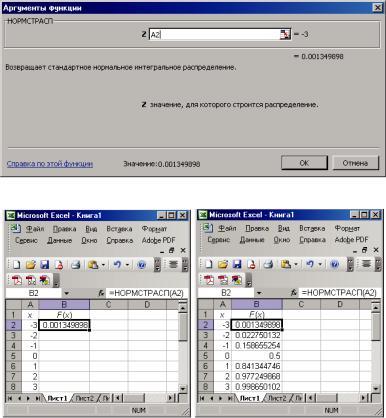
– при выделенной активной ячейке В2 (щелчок ЛКМ делает ее активной – выделяется прямоугольной жирной рамкой) обычный курсор Excel в виде белого крестика подводим к правому нижнему углу рамки выделения – маркеру заполнения в виде черного маленького квадрата, пока курсор мыши не превратится в «худой» черный крестик. При нажатой ЛКМ протаскиваем этот крестик по ячейкам В3:В8, копируя содержание функции в эти ячейки. Результат показан на рис. 1.5, б.
Рис. 1.4. Меню задания аргументов функции НОРМСТРАСП
а |
б |
Рис. 1.5. Результаты вычислений для примера 1.1:
а – задание функции в ячейке В2; б – результат копирования функции в ячейке В3:В8
19
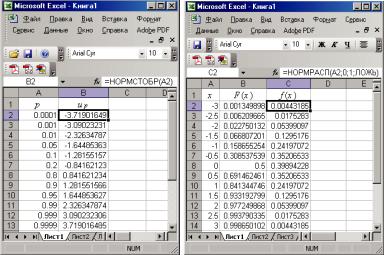
Пример 1.2. Вычислить с помощью функции НОРМСТОБР (р) квантили стандартного нормального распределения N
(0; 1) для значений р: 0,0001, 0,001, 0,01, 0,05, 0,1, 0,2, 0,8, 0,9, 0,95, 0,99, 0,999, 0,9999.
Решение: Зададим в ячейках A1, B1 названия столбцов,
вА2:А13 – заданные значения вероятностей, в ячейке В2 – функцию НОРМСТОБР(А2), копируя ее способом примера 1.1
вячейки В3:В13, имеем в столбце В результат, представленный на рис. 1.6, а.
Пример 1.3. Вычислить с помощью функций НОРМ-
РАСП (х; а; σ; ИСТИНА) и НОРМРАСП (х; а; σ; ЛОЖЬ)
функцию распределения F(x) и функцию плотности f (x) стандартного нормального распределения N (0; 1) для значений х от –3 до 3 с шагом 0,5.
а б
Рис. 1.6. Результаты вычислений для примеров 1.2 (а) и 1.3 (б)
Решение: Зададим в ячейках A1, B1, С1 названия столбцов, в А2 значение –3, в А3 –2,5, выделим эти обе ячейки и протаскиванием черного крестика – маркера заполнения при
20
