книги / Теория определяющих соотношений. Общая теория

71

10. Группа равноправности

Очевидно, каждая частица с -окрестностью тривиально изоморфна самой себе. Однако для каждой отдельной частицы Х (или Х – модельного тела) может существовать и нетривиальный изоморфизм, т. е. могут суще-

ствовать отличные друг от друга отсчетные конфигурации K 1 и K 2 для рассматриваемой частицы, такие, для которых соотношение

выполняется для любой невырожденной предыстории градиента деформа-

ции Ft (напомним, что F rT ). Поскольку в данном случае речь идет об одной и той же частице, обозначение частицы Х (или R0) исключено; предыстории деформации в левой и правой частях соотношения (45) одинаковы, но определяются по отношению к различным отсчетным конфигура-

циям ( K 1 и K 2 ).

Таким образом, согласно (45) реакция материала (напряжения) при одинаковых предысториях деформаций относительно двух различных конфигураций одной и той же частицы (с -окрестностью) будет одинаковой.

Например, для упруго-идеально-пластических материалов в качестве таких конфигураций могут быть использованы любые конфигурации после нагружения и полной разгрузки. Следует отметить, что здесь говорится о неотличимости конфигураций по реакции материала в макросмысле; при переходе на иной масштабный уровень (например, мезоили микроуровень) ситуация меняется: субструктура дефектов в сравниваемых конфигурациях может отличаться, однако эти отличия должны быть несущественными, чтобы поведение материала в макроэкспериментах было одинаковым.

Возникает вопрос о соответствии вводимого понятия с содержащимся в предыдущем разделе определением материального изоморфизма. В предыдущем определении устанавливался «пространственный изоморфизм», соответствие между различными частицами исследуемого тела. При этом частицы не различимы не только по реакции материала, но и «геометрически», т. е. не обладая никакой информацией о предшествую-

чить ни по взаиморасположению, ни по длинам материальных отрезков. Рассматриваемое в настоящем разделе соответствие (45) можно назвать изоморфизмом «по времени» (или «по параметру нагружения»). Здесь анализируется одна и та же частица в различных конфигурациях с неотли-

72

чимой реакцией материала. В то же время понятно, что геометрически эти конфигурации вполне различимы, одна получается из другой некоторым деформированием.

Таким образом, никакими макроэкспериментами по определению реакции материала вблизи точки Х тела B нельзя установить, из какой

конфигурации осуществляется деформирование — K 1 или K 2 . В этом

случае говорят, что конфигурации K 1 и K 2 равноправны в точке Х (по

равноправную и K , и K . Иначе говоря, суперпозиция операторов из MF

K

есть оператор того же множества. Очевидно, что множеству MF принад-

K

ассоциативности (знак й означает суперпозицию операторов). Показать последнее свойство нетрудно, учитывая, что отображения из множества MF представляют собой вектор–значные функции (аффинные преобразо-

K

том свойств множества отображений MF можно заключить, что это мно-

K

жество представляет собой группу относительно операции суперпози-

ции. Нетрудно увидеть, что свойство коммутативности не выполняется.

73

Группа MF называется группой равноправности материала по

K

отношению к K в точке Х, определяемой реакцией F . Иногда ее назы-

K

вают группой изотропии; однако следует иметь в виду, что речь не идет об изотропии материала (независимости реакции от ориентации материального объема по отношению к фиксированной в пространстве истории деформации, например), для анизотропных материалов также существуют группы равноправности.

Следует отметить, что обычно группой равноправности называют не

K

вышесказанному

В соответствие преобразованию с помощью вектор-значных функций ставится преобразование, осуществляемое с помощью градиентов i( ), определенных в соответствующих конфигурациях. Например, преоб-

o

разование конфигурации окрестности R в K в конфигурацию окрестно-

o

сти R2 в K 2 осуществляется следующим образом:

K

ции F ). При этом равноправные конфигурации должны иметь одинако-

K

вую плотность (поскольку плотность часто входит в качестве независимого аргумента определяющего отображения, и в противном случае не представляется возможным осуществить одинаковую историю воздействий из равноправных конфигураций; кроме того, различие в плотности двух конфигураций легко устанавливается в макроэкспериментах). Следовательно, градиенты рассматриваемых преобразований должны иметь единичный по модулю определитель

состоящая из градиентов всех отображений, переводящих K в равноправ-

ные конфигурации. Обозначим элементы этой группы через H, H g ; H

K

— унимодулярные (имеющие единичный по модулю определитель) тензоры второго ранга.

для любой невырожденной предыстории (FT )t . Подобное соотношение

можно получить для F (с использованием градиента обратного преобра-

K2

зования H-1). Однако в данном случае конфигурации K1 , K2 равноправны с точки зрения определяющего отображения и их можно отождествить с

отсчетной конфигурацией K рассматриваемой группы равноправности

g . Следовательно, соотношение (48) может быть преобразовано к виду

K

K K

В записи принципа независимости от системы отсчета (для определяющего отображения в Kt) можно положить Ot = O(t) = O = const, тогда получаем

являющееся необходимым условием для принадлежности ортогональных элементов группе g . Проводя рассуждения в обратном порядке, можно

K

76

показать, что если O удовлетворяет (53), то O g . Следовательно, усло-

K

вие (53) является необходимым и достаточным условием принадлежности

ортогонального тензора O группе равноправности g .

K

Отметим, что условие (53) по виду совпадает с определением изотропных функций, однако в последнем O — произвольные элементы O ; в

данном же случае O g ; кроме того, здесь Fo – произвольный оператор,

K K

а не тензорзначная функция.

Очевидно, что оператор инверсии (тензор (-E)) принадлежит группе

g , что непосредственно следует из (53):

K

Преобразование инверсии, очевидно, не отвечает никакой физически реализуемой деформации, однако с точки зрения формальной ничто не

физически реализуемых преображений с градиентами, определители кото-

рых равны (+1), то группу преобразований g можно представить прямым

K

произведением тривиальной группы (E,-E) на группу g :

Попутно показано, что наименьшая возможная группа равноправности есть (E, –E).

Вообще говоря, любая подгруппа унимодулярной группы может быть группой равноправности некоторого материала. Можно построить

бесконечное множество операторов реакции материала F , отвечающих

K

определенной произвольной подгруппе g .

K

Каждой конфигурации выделенной частицы (с малой окрестностью) в общем случае соответствуют, конечно, разные группы равноправности. Но поскольку речь идет об одной и той же материальной частице, то, естественно, возникает вопрос: а существует ли связь, соответствие групп равноправности по отношению к различным отсчетным конфигурациям (т.е.

не обязательно входящим в группу равноправности g отсчетной конфи-

K

гурации K ) для рассматриваемой произвольной частицы? Действительно, как и определяющее отображение F , группа равноправности g для вы-

K K

78

ваться в (58) в качестве некоторой произвольной предыстории, которую в

ностью) в двух конфигурациях K 1 и K 2 существует взаимно-

однозначное соответствие вида (61).

Кроме того, отсюда следует, что существование группы равно-

правности и ее «мощность» есть факты, не зависящие от выбора отсчетной конфигурации.

79

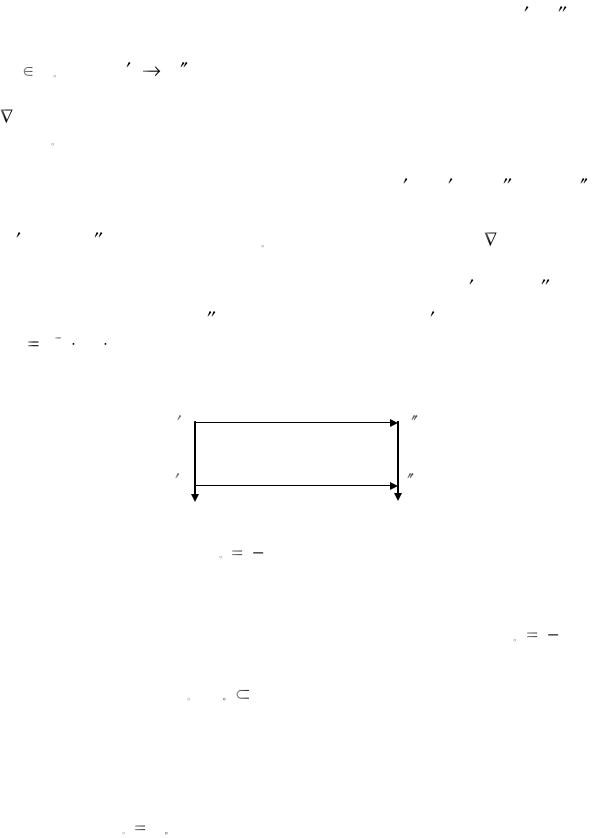
Прокомментируем полученный результат (61). Пусть K 1 ,K 1 — равноправные конфигурации, получаемые с помощью преобразования

Тогда реакция материала, определяемая из новой отсчетной конфигурации

группа равноправности не изменяется при объемном расширении или сжатии. Заметим, что, несмотря на совпадение групп равноправности, в