Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Решение электротехнических задач методом конечных элементов

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

944.52 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

H*	1	du .	(3.13)
	a
		dr

Аналитические выражения для напряженности магнитного поля одиночного цилиндрического проводника запишутся следующим образом [5]:

– при r 0 RC

H		I r		;	(3.14)
H	2 R		2	;	(3.14)
	2 R		2
		C
– при r RC
H		I	.		(3.15)
H		2 r	.		(3.15)
		2 r

Задание

Дан одиночный проводник (см. рис. 3.1), по которому протекает ток. Найти распределение магнитного потенциала и напряженности магнитного поля.

Варианты заданий представлены в табл. 3.1.

			Таблица 3.1
	Варианты заданий

Номер варианта	RC , мм	R0 , мм	I , A
1	11	50	1500
2	12	52	1750
3	13	54	2000
4	14	56	2250
5	15	58	2500
6	16	60	2750
7	17	62	3000
8	18	64	3250
9	19	66	3500
			21

			Окончание табл. 3.1

Номер варианта	RC , мм	R0 , мм		I , A
10	20	68		3750
11	21	70		4000
12	22	72		4250
13	23	74		4500
14	24	76		4750
15	25	78		5000
16	26	80		5250
17	27	82		5500
18	28	84		5750
19	29	86		6000
20	30	88		6250
21	31	89		6500
22	32	90		6750
23	33	91		7000
24	34	92		7250

Содержание отчета:

1.Титульный лист.

2.Задание.

3.Постановка задачи.

4.Аналитические формулы по определению напряженности магнитного поля.

5.Результаты вычислений.

Номер узла			r , мм		u , В с/м

Номер	r , мм	H*	, A/мм	H , A/мм	H * H	100 , %

элемента					H max
6. Графики u f (r) ,			H * f (r)	и H f (r) .

7.Код программы.

8.Выводы.

4. Двухмерная задача стационарной теплопроводности

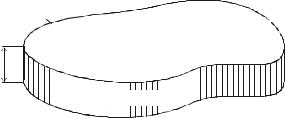
Рассмотрим задачу определения стационарного температурного поля в поперечном сечении кабеля (рис. 4.1).

Рис. 4.1. Трехжильный кабель: 1 – токопроводящая жила (ТПЖ); 2 – изоляция; 3 – межфазное заполнение; 4 – полимерная оболочка

Дифференциальное уравнение теплопроводности (1.1) в двухмерной стационарной постановке запишется как

0 .

(4.1)

Источником тепла является электрический ток, протекающий по токопроводящим жилам.

Применение метода Галёркина к уравнению (4.1) даст

qV dV 0 ,

(4.2)

где u – приближенное решение.

После преобразования уравнения (4.2) запишем

	N T	u	N	T	u	T	T	u
					dS N		qV dS N		dL 0 , (4.3)
	x	x	y		dS N		qV dS N	n	dL 0 , (4.3)
	x	x	y		y	S	L	n
S						S	L

где S – площадь поперечного сечения (рис. 4.2); L – внешний контур (см. рис. 4.2).

V=hS

Sb=hL

Рис. 4.2. Исследуемая область

На рис. 4.2 приведена произвольная двухмерная область исследования S . Здесь Sb – площадь боковой поверхности объема V;

dV hdS и dSb hdL .

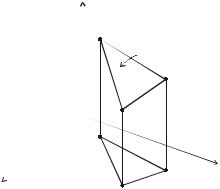
Интерполяционный полином для двухмерного симплексэлемента имеет вид (рис. 4.3) [2, 3]

u NiUi N jU j NkUk N U ,

(4.4)

где U – вектор-столбец узловых неизвестных;

ai bi x ci y ;

ai X jYk XkYj ;

или N

Y ;

2S(e)

c X

XkYi XiYk ;

N j

aj bj x cj

y ;

Yk Yi ;

или

(e)

Xi Xk ,

1	1	x	y

	1	X j	Yj	;
2S(e)
	1	Xk	Yk

			1	X	Y

N		1	1	xi	yi	;
	j	2S(e)
			1	Xk	Yk

ak XiYj X jYi ;

1 X

b x c y

;

или

1 X

;

2S(e)

X j Xi ,

1 x

Здесь S(e)

– площадь треугольного симплекс-элемента,

S(e) 1

1 X j

u=NiUi+NjUj+NkUk

(Xi ,Yi)

(Xk ,Yk)

(Xj ,Yj)

Рис. 4.3. Двухмерный симплекс-элемент

Матрица градиентов запишется следующим образом:

N j

Yj Yk

Yk Yi

X j

Xi Xk

(e)

Nk
x			1		bi	bj		bk
x			1		bi	bj		bk
					c c			c
			2S	(e)	c c		j	c
Nk			2S		i		j	k
y
y
Y	Y							(4.5)
i		j	.					(4.5)
X j	Xi

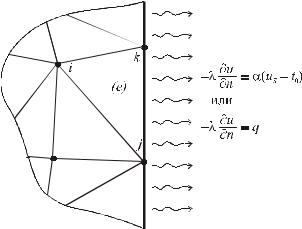
Как и при решении одномерной задачи стационарной тепло-

проводности,	интеграл	N T	u dL	в уравнении (4.3)	учитывает
		L	n
граничные	условия	второго	и	третьего родов	(рис. 4.4).
На рис. 4.4: q – заданная плотность теплового потока; uS					– искомая

температура границы тела; t0 – заданная температура окружающей среды; – коэффициент теплоотдачи.

Рис. 4.4. Поток тепла на границе области

Уравнение (4.3) с учетом выражений (4.4), (4.5) и граничных условий запишется следующим образом:

N T

dS U

N N dL U

N T qdL N T t0 dL N T qV dS 0.

(4.6)

Перепишем уравнение (4.6) в виде

B T B dS U N T N dL U

		S		L
	N T qdL			N T t0dL N T qV dS,	(4.7)
		Lq	L	S



	x
где B	N – матрица градиентов.

	y

Как и для одномерной задачи стационарной теплопроводности, принимаем, что коэффициент теплопроводности и мощность внутреннего источника тепла qV постоянны в пределах конечного

элемента.

Переход от выражения (4.7) к сумме интегралов по элементам дает следующие выражения:

	k	U f qV
	(e)	(e)
	(e)
		q
	k ( g ) U f ( g )

( g )

;

f ( g ) ,

(4.8)

(4.9)

где		k (e) B T B dS ;			f (qeV)			qV N T dS ;
		S( e )				S( e )
k ( g)		N T N dL ; f ( g )		t0	N T dL ; f ( g )			q N T dL .
					q
	L( g )		L( g )				L( g )
							q

Индекс (e) указывает на то, что суммирование производится по двухмерным конечным элементам, а индекс (g) отвечает за сум-

мирование по одномерным конечным элементам по границе расчетной области.

Определим члены уравнения для текущего элемента

k (e) B T B ds B T B ds B T B S(e)

S( e ) S( e )

1bibi cici

4S(e) bjbi cj cibk bi ck ci

bibj cicj bjbj cj cj bk bj ck cj

bibk	cick
b b	c c	.	(4.10)
j k	j k
b b	c c
k k	k k

Интеграл для локальных координат треугольного симплексэлемента определяется по формуле

S( e )

Тогда

f (qeV) qV N T S(e)


L a L b L cds				a!b!c!		2S(e) .
L a L b L cds			a	b c 2 !		2S(e) .
1	2	3

		N			L			q S
ds qV			i			1		q S
ds qV		N j ds qV			L2		ds	V
		S( e ) N			S( e) L			3
			k			3

(4.11)

(e) 1

1 . (4.12)

В выражении (4.9) производится суммирование по одномерным симплекс-элементам границы области исследования, для которых необходимо определить следующие матрицы:

k ( g)			N T N dL ; f ( g)		t0 N T dL	; f ( g )		q N T dL ,
						q
		L( g )		L( g )			L( g )
							q
где	N		– функция формы	одномерного		линейного		симплекс-

элемента. Указанные интегралы вычисляются аналитически с помощью выражения

	L1a L2bdL	a!b!	L( g ) ,	(4.13)
		a b 1 !
L( g )

где L( g ) – длина одномерного линейного конечного элемента, определяемая по формуле

L( g )

Xi X j 2 Yi Yj 2 .

(4.14)

Здесь индексы i и j – номера узлов одномерного элемента.

С учетом выражения (4.13) локальная матрица коэффициентов

k ( g ) , вектор-столбцы

( g )

и f ( g )

определятся

следующим

образом:

( g )

Ni2

Ni N j

L( g )

N dL

; (4.15)

( g )

( g ) Ni N j

N j

( g )

t L( g )

t0 N

N j

;

(4.16)

( g )

f (qg )

q N T dL q

qLq

(4.17)

L( g )

N j

Задание

На рис. 4.1 представлено поперечное сечение трехжильного кабеля. По токопроводящим жилам протекает электрический ток, который является источником теплового воздействия на кабель. На внешней поверхности кабеля задано граничное условие третьего рода – температура окружающей среды t0 и коэффициент теплоотдачи

. Необходимо определить ток в токопроводящих жилах, при котором максимальная температура была равна 70 °С, и построить температурное поле в поперечном сечении кабеля.

Варианты заданий представлены в табл. 4.1. Заданы коэффициенты теплопроводности элементов конструкции кабеля (см. рис. 4.1 и табл. 4.1). Для нечетных вариантов токопроводящие жилы медные, для четных – алюминиевые.

Формула для определения сопротивления жилы на единицу длины кабеля имеет вид [7]

R	ρ20	1	αT tЖ 20 ,	(4.18)
R	SЖ	1	αT tЖ 20 ,	(4.18)
	SЖ
				29

где ρ20 – удельное электрическое сопротивление при 20 °С, Ом м; SЖ – сечение жилы, м2; αT – температурный коэффициент электрического сопротивления, 1/°С; tЖ – температура токопроводя-

щей жилы.

Значения электрических удельных сопротивлений и температурных коэффициентов проводниковых материалов приведены в табл. 4.2.

Удельная мощность внутреннего источника тепла в токопроводящей жиле определяется согласно закону Джоуля – Ленца по формуле [7]

q	I 2	R / S	Ж	,	(4.19)
V	Ж		Ж

где IЖ – ток, А; R – электрическое сопротивление токопроводящей жилы, Ом/м; SЖ – площадь поперечного сечения токопроводящей

жилы, м2.

Определение сопротивления токопроводящей жилы R по формуле (4.18) и удельной мощности qV по формуле (4.19) следует прово-

дитьсучетомустановившейся температурытокопроводящейжилы. Геометрические параметры расчетной области и разбиение ее

на конечные элементы даны в электронной таблице.

Таблица 4.1

Варианты заданий

Номер	1 ,	2 ,	3 ,	4 ,	,		t0	, °С
варианта	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	2	·°С)	t0	, °С
варианта	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м	·°С)
1	384	0,3	0,1	0,2	15			22
2	204	0,2	0,1	0,2	16			21
3	384	0,15	0,1	0,2	17			20
4	204	0,3	0,1	0,2	18			19
5	384	0,2	0,1	0,2	19			18
6	204	0,15	0,1	0,2	20			17
7	384	0,3	0,1	0,2	21			16
8	204	0,2	0,1	0,2	22			15
30

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в папке книги

#
12.11.202312.71 Mб3Решение некоторых многоэкстремальных задач методом сужающихся окрестностей..pdf
#
12.11.202321.38 Mб4Решение нелинейных задач теории оболочек на ЭВМ..pdf
#
19.11.202332.73 Mб17Решение практических задач при бурении и освоении скважин..pdf
#
12.11.202312.02 Mб0Решение технологических проблем действующего производства средствами автоматизации. Производство калийных удобрений.pdf
#
12.11.20235.01 Mб1Решение частных задач оптимизации для инженерных систем зданий..pdf
#
12.11.2023944.52 Кб1Решение электротехнических задач методом конечных элементов..pdf
#
12.11.2023963 Кб6Риторика и ораторское искусство..pdf
#
12.11.20238.54 Mб1Робот. Компьютер. Гибкое производство.pdf
#
19.11.202351.95 Mб0Рок в Союзе 60-е, 70-е, 80-е..pdf
#
12.11.202310.45 Mб2Роликовые и дисковые конвейеры и устройства..pdf
#
12.11.20231.53 Mб1Роль фаворитизма в социальном процессе..pdf