
книги / Строительная механика машин
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет»
Е.В. Кузнецова, Г.Л. Колмогоров, Т.Е. Мельникова
СТРОИТЕЛЬНАЯ МЕХАНИКА МАШИН
Утверждено Редакционно-издательским советом университета
в качестве учебно-методического пособия
Издательство Пермского национального исследовательского
политехнического университета
2018
УДК 624.04(072.8) К89
Рецензенты:
д-р техн. наук, профессор В.Н. Трофимов (Пермский национальный исследовательский политехнический университет);
канд. физ.-мат. наук, доцент И.А. Оборина (Пермский военный институт войск Национальной гвардии РФ)
Кузнецова, Е.В.
К89 Строительная механика машин : учеб.-метод. пособие / Е.В. Кузнецова, Г.Л. Колмогоров, Т.Е. Мельникова. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2018. – 75 с.
ISBN 978-5-398-01969-8
Рассматриваются общие вопросы решения задач изгиба пластин, вопросы использования вариационных (энергетических) методов в cтроительной механике, приводятся основные уравнения пластин и оболочек с применением принципов Лагранжа, Кастильяно, метода Бубнова – Галеркина и др. Теоретические положения иллюстрируются примерами. Представлен лабораторный практикум по исследованию прогибов при нагружении квадратных и круглых пластин.
Предназначено для бакалавров и магистров очной и заочной форм обучения по направлению «Прикладная механика», изучающих курсы «Строительная механика машин», «Экспериментальная механика», «Прикладная механика».
УДК 624.04(072.8)
ISBN 978-5-398-01969-8 |
© ПНИПУ, 2018 |
2
ОГЛАВЛЕНИЕ |
|
Введение............................................................................................................ |
4 |
1. Теория пластин ........................................................................................... |
5 |
1.1. Основные понятия и определения в теории пластин...................... |
5 |
1.2. Цилиндрическая жесткость пластин................................................. |
7 |
1.3. Дифференциальное уравнение изогнутой поверхности |
|
поперечно нагруженной пластинки......................................................... |
9 |
1.4. Изгиб круглых пластин...................................................................... |
17 |
1.5. Учет граничных условий при расчете пластин................................ |
21 |
2. Вариационные методы в теории пластин и оболочек........................ |
24 |
2.1. Вариационные принципы строительной механики......................... |
24 |
2.1.1. Принцип Лагранжа – Кастильяно ........................................... |
24 |
2.1.2. Принцип Гамильтона................................................................ |
28 |
2.2. Теория вариационных методов.......................................................... |
31 |
2.3. Практическое приложение вариационных методов........................ |
37 |
2.3.1. Применение метода Ритца – Тимошенко............................... |
37 |
2.3.2. Канонические уравнения Галеркина |
|
для изгиба пластинки.......................................................................... |
41 |
2.3.3. Уравнения Кастильяно – Ритца для изгиба пластинки......... |
44 |
2.3.4. Уравнения устойчивости сжатой пластинки |
|
(уравнение Галеркина) ....................................................................... |
48 |
2.3.5. Энергетический метод расчетов на устойчивость................. |
50 |
2.3.6. Применение метода Бубнова – Галеркина для расчета |
|
пологих оболочек................................................................................ |
51 |
2.3.7. Применение метода Ритца – Тимошенко для расчета |
|
гибких пластин.................................................................................... |
54 |
3. Лабораторный практикум........................................................................ |
63 |
3.1. Выполнение и оформление лабораторных работ............................ |
63 |
3.2. Порядок выполнения и защиты лабораторных работ..................... |
65 |
3.3. Лабораторные работы......................................................................... |
66 |
Лабораторная работа № 1. Изгиб круглых пластин........................ |
66 |
Лабораторная работа № 2. Изгиб квадратных пластин................... |
69 |
Вопросы для самостоятельного изучения теоретического материала........ |
71 |
Вопросы к экзамену по дисциплине «Строительная механика машин» |
|
(направление подготовки «Прикладная механика», профили ДПМ, |
|
ВМ, БМ) ............................................................................................................. |
72 |
Список рекомендуемой литературы............................................................... |
74 |
3
ВВЕДЕНИЕ
Практически все задачи, связанные с исследованием напряжен- но-деформированного состояния в строительных конструкциях, сводятся к решению краевых задач для одного или нескольких дифференциальных уравнений для стержней, пластин и оболочек. Точное решение этих уравнений не вызывает затруднения лишь в некоторых элементарных случаях. В более сложных случаях оно сопряжено с большими математическими трудностями, для большинства же задач точное решение вообще невозможно. Во всех таких случаях приходится прибегать к методам приближенного решения задачи.
Методы приближенного решения краевых задач дифференциальных уравнений могут быть разбиты на две большие группы:
а) методы вариационные, дающие приближенное аналитическое выражение для искомой функции;
б) методы численные, дающие численные значения функции при тех или иных значениях аргумента.
К первой группе относятся метод Ритца, метод Галеркина, метод Треффца, Канторовича и другие, а ко второй – конечно-разност- ный метод или метод сеток, вариационно-разностный метод, метод конечных элементов.
В данном пособии рассматриваются методы первой группы.
4

1.ТЕОРИЯ ПЛАСТИН
1.1.Основные понятия и определения в теории пластин
Раздел «Теория пластин» входит в комплексную дисциплину «Строительная механика машин» направления бакалавриата «Прикладная механика».
Существует большое количество деталей конструкций, машин и механизмов с определенными характеристиками и свойствами, которые при моделировании и абстрагировании можно описать как пластины. Конструкции с использованием деталей, подобных пластинам, легкие, прочные и широко используются в строительстве, аэрокосмической технике, судостроении, автомобильной промышленности. Расчет пластин на прочность, жесткость и устойчивость – это задачи строительной механики.
Пластина – это модель формы, к которой можно отнести тела, у которых один габаритный размер (толщина h) много меньше двух других (ширины а и длины b) (рис. 1.1).
z
a
b
x
h
у
Рис. 1.1. Прямоугольная пластина с размерами h×a×b
Определяющими характеристиками для пластин являются (см. рис. 1.1): срединная поверхность – плоскость, равноудаленная от наружных поверхностей, а также толщина h и величина прогиба w при действии нагрузки.
5
В зависимости от величины прогиба пластинки подразделяют на три группы:
1) жесткие пластины, у которых величина прогибов не пре-
вышает 20–25 % от толщины пластинки |
|
1 |
÷ |
1 |
|
|
, |
в них |
|
w ≈ |
4 |
5 |
h |
||||||
|
|
|
|
|
|
|
|
||
преобладают изгибные напряжения, зависимость между прогибами и нагрузкой линейна;
2) гибкие |
пластины, для которых величина прогибов |
|||
1 |
÷ |
1 |
|
в них возникают цепные (мембранные) напряжения, |
w > |
|
h, |
||
4 |
|
5 |
|
|
действующие в плоскости срединной поверхности; 3) абсолютно гибкие пластины, у которых прогиб при дейст-
вии нагрузки в 5–6 раз больше их толщины (w >(5 ÷6) h) , зависи-
мость между прогибами и нагрузкой нелинейна, в них преобладают мембранные напряжения, а изгибными напряжениями можно пренебречь.
В тех случаях, когда прогибы малы в сравнении с толщиной, т.е. речь идет о жестких пластинах, можно построить удовлетворительную приближенную теорию изгиба под поперечными нагрузками, основываясь на следующих допущениях:
1.В срединной плоскости пластинка не испытывает деформаций. При изгибе эта плоскость остается нейтральной.
2.Точки пластинки, лежащие до нагружения на нормали к срединной плоскости, остаются в процессе изгиба на нормали к ее срединной поверхности. Это допущение эквивалентно пренебрежению влиянием перерезывающих сил на прогиб пластинок, что допустимо, за исключением случая пластины с отверстием, когда перерезывающие силы имеют большое значение.
3.Нормальными напряжениями σz в направлении, перпенди-
кулярном к плоскости срединной поверхности пластинки, допустимо пренебрегать (σz = 0).
6

Основываясь на этих допущениях, можно все компоненты напряжений выразить через прогибы пластинки.
1.2. Цилиндрическая жесткость пластин
Рассмотрим задачу об изгибе длинной прямоугольной пластинки толщиной h, несущей поперечную, не изменяющуюся по длине пластинки нагрузку Р(х). Изогнутую поверхность участка такой
пластинки, достаточно удаленного |
|
l |
|||||
от ее концов, можно при этом счи- |
|
||||||
|
|
|
|||||
тать цилиндрической с |
осью ци- |
|
|
x |
|||
|
|
||||||
линдра, |
параллельной |
пластинке |
|
|
|||
|
dy |
||||||
(рис. 1.2). |
|
|
|
|
|||
|
|
|
|
|
|
||
Для |
вывода |
дифференциаль- |
|
|
|
||
ного уравнения |
изгиба |
выделим |
|
w |
|||
в пластине элементарную полоску, |
y |
||||||
|
|
||||||
как стержень прямоугольного по- |
|
|
|
||||
перечного сечения с пролетом l и |
|
z |
|||||
толщиной h. При вычислении обу- |
Рис. 1.2. Изгиб прямоугольной |
||||||
словленных изгибом напряжений |
|||||||
в таком стержне мы предполагаем, |
|
пластины |
|||||
|
|
|
|||||
что поперечные сечения стержня остаются плоскими, испытывая лишь повороты относительно своих нейтральных осей.
Если в концевых сечениях стержня не приложено никаких нормальных сил, то нейтральная поверхность стержня совпадает со срединной поверхностью пластинки, и относительное удлинение волокна, параллельного оси х, окажется пропорциональным его расстоянию от срединной поверхности. Кривизну изогнутой оси
стержня можно будет при этом принять равной d 2 w/dx2 . Относительное удлинение волокна, отстоящего на расстоянии z от срединной поверхности (рис. 1.3), будет иметь вид
εх = −z d 2 w . dx2
7

h
2 |
M |
M |
|
||
h |
σx z dz |
|
2 |
σx |
a |
б |
Рис. 1.3. Относительное удлинение волокна (а) в сечении прямоугольной пластины от действия нормальных напряжений (б)
Пользуясь законом Гука, выразим относительные удлинения εх и εy заштрихованного на рис. 1.3, а элемента в функции действующих на него нормальных напряжений:
εх = |
1 |
(σх −µσу ), |
|
E |
|||
|
(1.1) |
||
|
|
εy = E1 (σy −µσx ) = 0 ,
где µ – коэффициент Пуассона, Е – модуль упругости.
Для того чтобы пластинка сохранила при деформации непрерывность, необходимо, чтобы поперечная линейная деформация ее в направлении у была равна нулю. Поэтому из второго из уравнений (1.1) напряжение σу =µσх . Подставив это значение в первое, по-
лучим:
εх = |
1 |
(σх −µσy ) = |
1−µ2 |
σх или σх = |
E |
|
εх , |
(1.2) |
E |
E |
1−µ |
2 |
|||||
|
|
|
|
|
|
где εx – относительное удлинение волокна, отстоящего на расстоянии z от срединной поверхности.
8

Располагая выражением для напряжения изгиба σх , находим
посредством интегрирования изгибающий момент в элементарной полоске:
h 2 |
h 2 |
|
E d |
2 |
w dz = − |
Eh |
3 |
d |
2 |
w |
|
|||
М = ∫ |
σx z dz = − ∫ z2 |
|
|
|
|
. (1.3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
12(1−µ2 ) dx2 |
|||||||||
−h 2 |
−h 2 |
1−µ2 dx2 |
|
|||||||||||
Вводя следующее обозначение: |
|
|
|
|
|
|
|
|
||||||
|
|
|
Eh3 |
|
|
|
|
|
|
|
|
|||
|
|
|
= D, |
|
|
|
|
|
(1.4) |
|||||
|
12(1−µ2 ) |
|
|
|
|
|
||||||||
представим уравнение изогнутой кривой, т.е. кривой прогибов, для элементарной полоски в следующем виде:
D d 2 w |
= −M . |
(1.5) |
dx2 |
|
|
Здесь величина D играет ту же роль, что и произведение El, входящее в формулы изгиба балки, и называется цилиндрической жесткостью пластины при изгибе.
1.3. Дифференциальное уравнение изогнутой поверхности поперечно нагруженной пластинки
Рассмотрим изгиб пластинки, нагруженной поперечной силой. Пластинка свободно опирается по контуру, т.е. опорные реакции на краях должны быть нормальны к пластинке. Прогибы при этом примем малыми в сравнении с толщиной. При этих условиях можно пренебречь деформацией в срединной плоскости пластины.
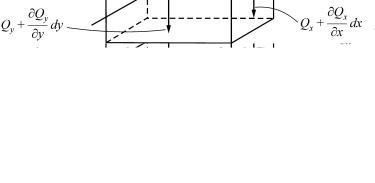
Рассмотрим элемент, вырезанный из пластинки, как показано на рис. 1.4.
Кроме изгибающих и крутящих моментов, в данном случае будут действовать еще и вертикальные перерезывающие силы, приложенные по боковым граням элемента:
9
|
h |
|
|
h |
|
|
Qx = |
2 |
τxz dz, |
Qy = |
2 |
τyz dz , |
|
∫ |
∫ |
(1.6) |
||||
|
−h |
|
|
−h |
|
|
|
2 |
|
|
2 |
|
|
где τхz, τyz – касательные напряжения.
Рис. 1.4. Элемент пластины, вырезанный двумя парами плоскостей, параллельных плоскостям xz и yz
Поскольку моменты и перерезывающие силы являются функциями координат х и у, то при исследовании условий равновесия элемента мы должны принять во внимание малые изменения этих величин, обусловленные изменениями координат на малые величи-
ны dx и dy.
Срединная плоскость элемента представлена на рис. 1.5, где указаны те направления сил и моментов, которые принимаются положительными.
Рассмотрим действие нагрузки, распределенной по верхней поверхности пластинки. Интенсивность этой нагрузки обозначим через q, так что нагрузка, действующая на элемент поверхности, будет равна qdxdy.
Проектируя все приложенные к элементу силы на ось z, получим следующее уравнение равновесия:
10
