
книги / Программирование. Обработка информации в пакетах прикладных программ
.pdf
функции; t – значение аргумента, при котором вычисляется интерполирующее значение функции.
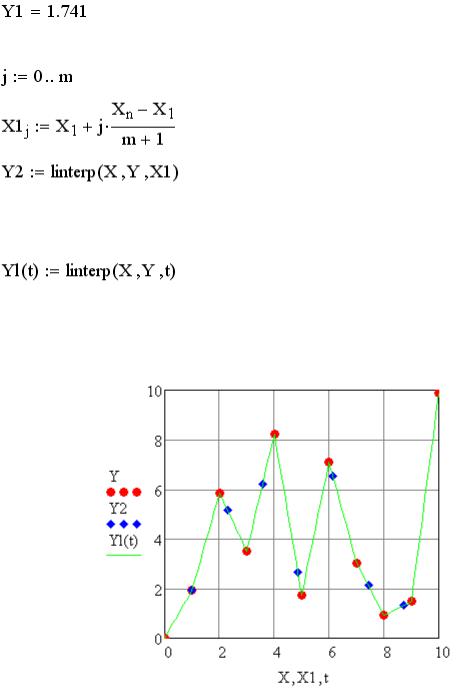
Кубическая сплайн-интерполяция для примера 1:
Пример 2. Решить задачу интерполяции для массива значений (X,Y), заданных с помощью функции случайных чисел rnd.
Решение.
Линейная интерполяция для примера 2:
21
1. 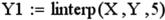 Y1 – интерполирующее значение функции в одной точке X=5
Y1 – интерполирующее значение функции в одной точке X=5
2. 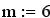
Y2 – массив интерполирующих значений функции в m точках значений X
3. 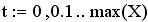
Y1(t) – непрерывная интерполирующая функция
22
Кубическая сплайн-интерполяция для примера 2:
Контрольные вопросы по лабораторной работе № 3
1.Сформулируйте задачу интерполяции.
2.Укажите требования к интерполирующей функции.
3.В чем заключается алгоритм проверки правильности полученного решения задачи интерполяции?
4.Опишите последовательность действий для решения задачи интерполяции (линейной и кубической сплайн-интерполяции) в программе Mathcad.
23

Лабораторная работа № 4
Аппроксимация табличных зависимостей методом наименьших квадратов
Цели работы:
–научиться использовать методы, языки и системы программирования для решения задачи аппроксимации табличных зависимостей;
–научиться использовать математический пакет Mathcad для решения задачи аппроксимации табличных зависимостей.
Задание.
1. Аппроксимировать табличную зависимость методом наименьших квадратов на языке программирования PascalABC.NET. Блок-схема алгоритма аппроксимации табличных зависимостей многочленом степени m для n точек методом наименьших квадратов приведена на рис. 10 [1]. Записать зависимость y f (x)
с полученными в результате расчета коэффициентами. В программе должна быть предусмотрена проверка правильности полученных решений (определить разность между табличными значениями y и значениями функции, вычисленными в таб-
личных значениях x по полученной зависимости y f (x) ).
2. Решить задачу аппроксимации табличной зависимости в математическом пакете Mathcad [3].
Варианты заданий
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
|||||
x |
y |
x |
y |
x |
y |
x |
y |
x |
y |
0,2 |
9,9 |
0,2 |
6,9 |
0,2 |
6,9 |
0,8 |
36,4 |
0,2 |
0,017 |
0,4 |
5,1 |
0,4 |
4,6 |
0,4 |
2,1 |
0,9 |
27,68 |
0,4 |
0,072 |
0,6 |
3,2 |
0,6 |
3,57 |
0,6 |
0,23 |
1,0 |
22,07 |
0,6 |
0,199 |
0,8 |
2,6 |
0,8 |
3,35 |
0,8 |
–0,4 |
1,5 |
11,48 |
0,8 |
0,276 |
1,0 |
1,9 |
1,0 |
2,9 |
1,0 |
–1,1 |
2,0 |
8,05 |
1,0 |
0,037 |
2,0 |
1,1 |
2,0 |
2,6 |
2,0 |
–1,9 |
2,5 |
6,78 |
2,0 |
0,6 |
4,0 |
0,4 |
4,0 |
2,15 |
4,0 |
–2,6 |
3,0 |
5,74 |
4,0 |
0,789 |
6,0 |
0,43 |
6,0 |
2,27 |
6,0 |
–2,57 |
3,5 |
5,41 |
6,0 |
0,836 |
8,0 |
0,15 |
8,0 |
2,03 |
8,0 |
–2,85 |
4,0 |
4,85 |
8,0 |
0,982 |
10,0 |
0,3 |
10,0 |
2,2 |
10,0 |
–2,7 |
4,5 |
4,78 |
10,0 |
0,905 |
24
Вариант 6 |
|
|
Вариант 7 |
Вариант 8 |
Вариант 9 |
Вариант 10 |
|||||||||||
x |
y |
|
|
x |
y |
x |
y |
x |
|
|
y |
x |
|
y |
|||
0,6 |
|
11,21 |
|
0,2 |
–2,32 |
0,2 |
2,12 |
0,2 |
|
–1,21 |
0,6 |
|
|
–2,32 |
|||
0,7 |
|
8,06 |
|
0,4 |
–0,73 |
0,4 |
0,93 |
0,4 |
|
–0,32 |
0,7 |
|
|
–0,73 |
|||
0,8 |
|
6,35 |
|
0,6 |
–0,12 |
0,6 |
0,02 |
0,6 |
|
–0,01 |
0,8 |
|
|
–0,12 |
|||
0,9 |
|
4,84 |
|
0,8 |
0,65 |
0,8 |
–0,45 |
0,8 |
|
0,38 |
0,9 |
|
0,65 |
||||
1,0 |
|
4,1 |
|
1,0 |
0,9 |
1,0 |
–1,1 |
1,0 |
|
0,5 |
1,0 |
|
0,9 |
||||
2,0 |
|
0,9 |
|
3,0 |
3,3 |
3,0 |
–3,1 |
3,0 |
|
1,7 |
2,0 |
|
3,3 |
||||
3,0 |
|
0,54 |
|
5,0 |
4,12 |
5,0 |
–4,32 |
5,0 |
|
2,01 |
3,0 |
|
4,12 |
||||
4,0 |
|
0,15 |
|
7,0 |
4,98 |
7,0 |
–4,79 |
7,0 |
|
2,55 |
4,0 |
|
4,98 |
||||
5,0 |
|
0,26 |
|
9,0 |
5,29 |
8,0 |
–5,26 |
8,0 |
|
2,48 |
5,0 |
|
5,29 |
||||
6,0 |
|
0,01 |
|
11,0 |
5,9 |
9,0 |
–5,29 |
9,0 |
|
2,79 |
6,0 |
|
5,9 |
||||
|
|
Начало |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i = 1, m+1 |
|
|
|
|
||
|
|
Ввод n, m, |
|
|
|
|
|
|
|
|
|
||||||
|
|
x(n), y(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w1 = n |
|
|
|
|
|
j = 1, m+1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 1, n
k = i + j – 1 aij = wk
b1 = b1 + yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод Гаусса |
|
|
|
i = 2, 2 m+1 |
|
|
|
|
|
|
|
|
|
|
|
i = 1, m+1 |
|
||||
|
|
|
|
|
|
|||
k = 1, n |
|
|
|
Вывод |
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
ai-1= , bi |
|
||
wi = wi + xki–1 |
|
|
|
|||||
|
|
|
|
|
|
|
||
|
|
нет |
|
|
|
|
|
|
i m+1 |
|
Конец |
|
|||||
|
|
|
|
|||||
|
да |
|
|
|
|
|
|
|
bi = bi + yk xki–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
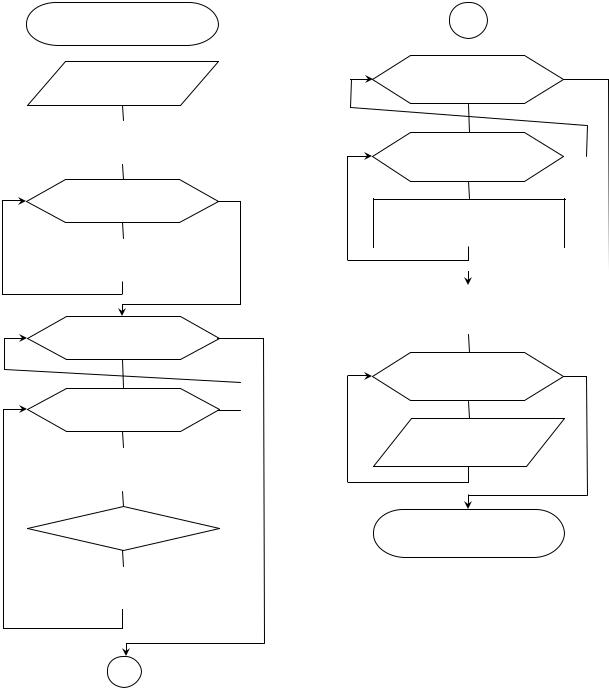
Рис. 10. Блок-схема алгоритма аппроксимации табличных зависимостей многочленом степени m для n точек методом наименьших квадратов
25
Блок-схема алгоритма аппроксимации табличных зависимостей многочленом степени m для n точек методом наименьших квадратов приведена на рис. 10.
Решается система уравнений вида (в матричной форме):
A z b ,
где
|
|
n |
n |
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
xi |
xi2 |
... |
xim |
|
|
|
|
|
|
yi |
|
|
|
||
n |
|
|
|
|
|
|
|
|
||||||||
|
|
i 1 |
i 1 |
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
n |
n |
|
n |
|
|
|
|
a0 |
|
n |
xi |
|
||
|
xi |
xi2 |
xi3 |
... |
xim |
1 |
|
|
|
|
yi |
|
|
|||
i 1 |
i 1 |
i 1 |
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
||
|
n |
n |
n |
|
n |
|
|
|
|
a1 |
|
|
n |
xi2 |
|
|
A |
xi2 |
xi3 |
xi4 |
... |
xim |
2 |
|
, |
z a2 |
|
, b |
yi |
|
, |
||
|
|
i 1 |
i 1 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
... |
|
i 1 |
|
|
|
|||||
................................................................................... |
|
|
|
|
am |
|
............. |
|
|
|||||||
|
n |
n |
n |
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
xim |
xim 1 |
xim 2 |
... |
xi2 m |
|
|
|
|
yi |
xim |
|
||||
i 1 |
i 1 |
i 1 |
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A – матрица коэффициентов системы; z – столбец неизвестных; b – столбец свободных членов.
В связи с тем, что матрица коэффициентов системы уравнений aij содержит попарно повторяющиеся элементы, для ее формирования используется вспомогательный массив w – вектор с количеством элементов, равным 2m 1. Кроме этого, в блок-схеме использованы следующие обозначения: векторы x и y – исходные табличные данные; n – количество точек таблицы; m – степень многочлена (аппроксимирующей функции); bi – вектор свободных членов. В результате выполнения приведенного на рис. 10 алгоритма получаем коэффициенты многочлена:
a0 = b1, a1 = b2, …, am = bm+1.
Полученные в результате значения a0, a1, …, am подставляют в аппроксимирующую функцию (в данной лабораторной работе это алгебраический многочлен Pm(x)), что позволяет полностью ее определить и в дальнейшем использовать для приближенного вычисления значений функции при значениях аргумента, отличных от таблично заданных, а также исследовать методами математического анализа.
26
Аппроксимация табличных зависимостей в программе Mathcad
При проведении различных экспериментов часто требуется массив экспериментальных данных (табличную зависимость) представить в виде функции, которую можно использовать в дальнейших расчетах. Если кривая, описываемая этой функцией, не должна проходить через все экспериментальные точки и является аппроксимацией (усреднением) исходных данных, операция получения промежуточных точек и расчетной функции называется регрессией. Регрессия сводится
кподбору коэффициентов в той или иной аналитической зависимости.
Впрограмме Mathcad есть несколько встроенных функций регрессии двух
типов:
1) позволяющих увидеть аналитическую зависимость, т.е. возвращающих набор коэффициентов аппроксимирующей функции;
2) не позволяющих увидеть аналитическую зависимость.
Рассмотрим функцию 2-го типа, которая не выводит коэффициентов и аппроксимирует массив данных одним многочленом степени n. В программе Mathcad это реализуется комбинацией встроенных функций интерполяции и регрессии:
interp(s,X,Y,t)
regress(X,Y,n)
Здесь X – вектор экспериментальных значений аргумента, расположенных в порядке возрастания; Y – вектор экспериментальных значений функции; s – вектор коэффициентов для построения аппроксимирующего многочлена, создаваемый функцией regress; t – значение аргумента, при котором вычисляется значение функции; n – степень аппроксимирующего многочлена.
Пример. Решить задачу аппроксимации для массива значений (X,Y), заданных с помощью функции случайных чисел rnd.
Решение.
27
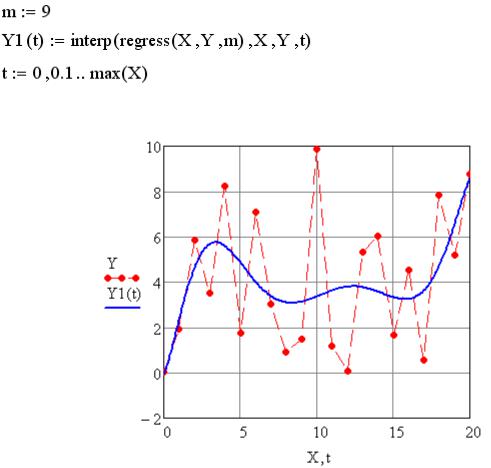
Поменяйте m – степень многочлена и проанализируйте изменения вида аппроксимирующей функции.
Контрольные вопросы по лабораторной работе № 4
1.Сформулируйте задачу аппроксимации табличных зависимостей.
2.Укажите требования к аппроксимирующей функции.
3.Опишите метод наименьших квадратов для аппроксимации таблично заданной функции.
4.В чем заключается алгоритм проверки правильности полученного решения задачи аппроксимации табличных зависимостей?
5.Опишите последовательность действий для аппроксимации табличных зависимостей в программе Mathcad.
28
Лабораторная работа № 5
Численные методы решения дифференциальных уравнений и их систем
Цели работы:
–научиться использовать численные методы, языки и системы программирования для решения обыкновенных дифференциальных уравнений и их систем;
–научиться использовать математический пакет Mathcad для решения обыкновенных дифференциальных уравнений и их систем.
Задание.
1.Решить дифференциальное уравнение методом Эйлера на языке программирования PascalABC.NET. Блок-схема алгоритма решения дифференциального уравнения 1-го порядка методом Эйлера приведена на рис. 11 [1]. В программе должна быть предусмотрена проверка правильности полученных решений (сравнить полученные значения искомой функции с точным решением, приведенным
втаблице заданий).
2.Решить дифференциальное уравнение методом Рунге–Кутты в математическом пакете Mathcad с помощью функций rkfixed и odesolve [3].
Варианты заданий
№ |
Дифференциальное |
Начальные |
Отрезок |
Шаг |
Точное решение |
|
||||||||||||
ва- |
уравнение |
|
условия |
интегри- |
интегри- |
|
|
|
y=f(х) |
|
|
|
||||||
ри- |
|
|
|
|
рования |
рования |
|
|
|
|
|
|
|
|
|
|
|
|
анта |
|
|
|
|
x0; xk |
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y y 1 |
ex |
yo |
2,5 |
|
|
f (x) cos x sin x |
|
1 |
x |
||||||||
|
y' |
1,5 |
0; 1 |
0,05 |
1 2 e |
|
||||||||||||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y" 4 y cos3x |
yo |
0,8 |
0; 1 |
0,05 |
f (x) cos 2x sin 2x 0, 2 cos3x |
||||||||||||
|
yo' |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
y" y ' 6 y |
2e4 x |
yo |
1, 433 |
0; 1 |
0,05 |
f (x) 0,1e3x |
e 2 x |
1 |
e4 x |
|
|||||||
|
y' |
0,367 |
3 |
|
||||||||||||||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
y" 2 y ' y |
5xex |
yo |
1 |
0; 1 |
0,05 |
f (x) ex |
xex |
|
5 |
x3ex |
|
||||||
|
yo' |
2 |
6 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
y" y ' 6y |
3x2 x 1 |
yo |
0,9 |
0; 1 |
0,05 |
f (x) 0,1e2 x |
e 3x 0,5x2 |
|
|||||||||
|
y' |
3, 2 |
|
|||||||||||||||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
8y" 2 y ' 3y x 5 |
yo |
1/ 9 |
0; 1 |
0,05 |
f (x) e |
x |
e |
3x |
|
|
x 17 |
|
|||||
|
|
|
||||||||||||||||
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
||||||
|
yo' |
7 /12 |
3 9 |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||
29
7 |
y" 4 y ' 5y 3x |
|
yo |
1, 48 |
|
|
|
2 x |
|
3 |
12 |
|
|
y' |
3, 6 |
0; 0,5 |
0,025 |
f (x) e |
|
(cos x sin x) |
5 x |
25 |
|
|
|
|
o |
|
|
|
|
|
|
|
|
8 |
y" 4y ' 4 y 0 |
|
yo |
1 |
0; 1 |
0,05 |
f (x) (1 x) e 2 x |
|
|
||
|
|
yo' |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
9 |
(1 x2 ) y " ( y ')2 1 |
0 |
yo |
1 |
0; 0,5 |
0,025 |
f (x) 1 x 2ln(1 x) |
|
|
||
|
yo' |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
10 |
y" 2 y ' 2 y 2e x |
cos x |
yo |
1 |
0; 1 |
0,05 |
f (x) e x (cos x sin x x sin x) |
||||
|
yo' |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
Примечание: заданное дифференциальное уравнение 2-го порядка при решении численным методом Эйлера необходимо привести к системе дифференциальных уравнений 1-го порядка. При этом формула метода Эйлера используется для каждого из полученных уравнений. Совместная система уравнений на каждом шаге интегрирования решается одновременно.
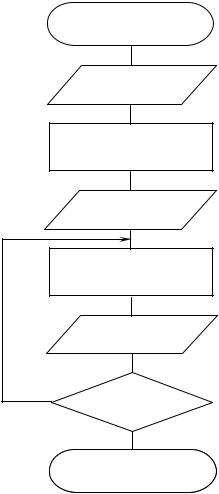
Алгоритм решения дифференциального уравнения 1-го порядка методом Эйлера представляет собой циклический процесс вычислений искомой функции y по формуле метода Эйлера при изменении аргумента x от x0 до xk с шагом h (рис. 11).
Начало
Ввод h, x0, xk, y0
x = x0 y = y0
Вывод x, y
y= y+h f(x,y) x = x+h
Вывод x, y
нет
x > xk
да
КОНЕЦКонец
Рис. 11. Блок-схема алгоритма решения дифференциального уравнения 1-го порядка методом Эйлера
30
