
книги / Метод конечных элементов для решения электротехнических задач
..pdfМинистерство науки ивысшего образования РоссийскойФедерации
Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет»
А.Г. Щербинин
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РЕШЕНИЯ ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧ
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета
2020
1
УДК 621.3:517.962.1(075.8) Щ64
Рецензенты:
д-р техн. наук, профессор Н.М. Труфанова (Пермский национальный исследовательский политехнический университет);
канд. техн. наук, ген. директор В.Г. Савченко (ООО «Богословский кабельный завод», г. Краснотурьинск)
Щербинин, А.Г.
Щ64 Метод конечных элементов для решения электротехнических задач : учеб. пособие / А.Г. Щербинин. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2020. – 105 с.
ISBN 978-5-398-02366-4
Рассмотрено применение метода конечных элементов для решения электротехнических задач.
Предназначено для бакалавров и магистров высших учебных заведений направлений подготовки 13.03.02, 13.04.02 «Электроэнергетика и электротехника», профилей «Конструирование и технологии
вэлектротехнике» и «Управление и информационные технологии
вэлектротехнике», а также для научных и инженерных работников, аспирантов, специалистов в области инженерных наук.
УДК 621.3:517.962.1(075.8)
ISBN 978-5-398-02366-4 |
ПНИПУ, 2020 |
2
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ............................................................................................. |
5 |
1. КОНЦЕПЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ.................. |
6 |
2. ДИСКРЕТИЗАЦИЯ ОБЛАСТИ........................................................ |
8 |
2.1. Типы конечных элементов................................................... |
8 |
2.2. Одномерный симплекс-элемент......................................... |
10 |
2.3. Двухмерный треугольный симплекс-элемент.................. |
14 |
2.4. Двухмерный четырехугольный элемент........................... |
19 |
2.5. Интерполяционные полиномы |
|
для дискретизованной области ................................................. |
24 |
3. ПРИМЕНЕНИЕ МЕТОДА ГАЛЁРКИНА |
|
В МЕТОДЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ........................................... |
27 |
4. РЕШЕНИЕ ОДНОМЕРНЫХ СТАЦИОНАРНЫХ |
|
ЗАДАЧ МКЭ......................................................................................... |
29 |
4.1. Теплопроводность плоской стенки.................................... |
29 |
4.2. Электрическое поле коаксиального кабеля...................... |
34 |
4.3. Осесимметричная задача магнитостатики........................ |
39 |
5. РЕШЕНИЕ ДВУХМЕРНЫХ СТАЦИОНАРНЫХ |
|
ЗАДАЧ МКЭ......................................................................................... |
45 |
5.1. Решение двухмерной задачи электростатики |
|
с использованием симплекс-элемента............................... |
45 |
5.2. Решение стационарной двухмерной задачи |
|
теплопроводности с использованием |
|
четырехугольного элемента................................................ |
50 |
5.3. Решение двухмерной задачи магнитостатики |
|
с использованием симплекс-элемента............................... |
60 |
5.4. Решение двухмерной осесимметричной задачи |
|
теплопроводности с использованием симплекс-элемента..... |
65 |
6. РЕШЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ЗАДАЧ |
|
С ГАРМОНИЧЕСКИ ИЗМЕНЯЮЩИМСЯ |
|
ПО ВРЕМЕНИ ПОЛЕМ МКЭ............................................................. |
72 |
3
6.1. Уравнения в переменном электромагнитном поле.......... |
72 |
6.2. Решение одномерной осесимметричной |
|
магнитодинамической задачи............................................. |
77 |
6.3. Решение двухмерной магнитодинамической задачи |
|
с использованием симплекс-элемента............................... |
86 |
7. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ.......................... |
93 |
7.1. Решение нестационарной одномерной |
|
осесимметричной задачи теплопроводности.................... |
93 |
7.2. Решение нестационарной двухмерной задачи |
|
теплопроводности с использованием |
|
симплекс-элементов .......................................................... |
100 |
СПИСОК ЛИТЕРАТУРЫ.................................................................. |
103 |
4
ВВЕДЕНИЕ
Решение задач электротехники зачастую связано с определением электромагнитных и температурных полей в исследуемой области. При этом наиболее эффективным подходом при решении подобного типа задач является использование численных методов, таких как метод конечных разностей и метод конечных элементов.
При решении задач со сложной геометрией более предпочтительным является метод конечных элементов (МКЭ). Широкому распространению метода конечных элементов способствовало применение метода взвешенных невязок (метод Галёркина), в результате чего МКЭ превратился в общий метод численного решения дифференциальных уравнений в частных производных.
Метод конечных элементов может быть использован также при решении электро- и магнитодинамических задач, задач нестационарной теплопроводности.
Основная идея метода конечных элементов базируется на том, что любую непрерывную функцию, такую как температура, электрический или магнитный потенциал, давление и др., аппроксимируют кусочно-гладкой (кусочно-непрерывной) функцией, определяемой на заданном количестве подобластей, которые называются конечными элементами. В пределах своего конечного элемента ку- сочно-гладкая функция представляет собой полином, а за его пределами равна нулю. Порядок полинома определяется типом конечного элемента. Достаточно часто в качестве аппроксимирующего полинома используется полином первой степени. Подбор параметров аппроксимирующих полиномов должен обеспечивать непрерывность функции по границам конечных элементов. В результате решения задачи методом конечных элементов вычисляется значение искомой функции в узлах конечных элементов.
5

1. КОНЦЕПЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Суть метода конечных элементов рассмотрим на примере определения электрического потенциала (x) между двумя плоскими
электродами (область 0 ), представленного на рис. 1.1. На рис. 1.2 показано разбиение области исследования на конечные элементы. Искомая функция (x) аппроксимируется функцией u(x) , которая
представляет собой сумму кусочно-непрерывных функций u(k ) |
[1–4]: |
u(x) u(k ) . |
(1.1) |
Как видно из рис. 1.2, область исследования разбита на четыре конечных элемента (в общем случае разной длины) с тремя внутренними и двумя внешними узлами.
Необходимо отметить, что для рассматриваемого примера в пределах текущего конечного элемента кусочно-непрерывная
функция u(k ) представляет собой полином первой степени, а за его пределами u(k ) 0 (рис. 1.3). При этом коэффициенты линейного полинома определяются значениями функции U1 , U2 , …, U5 в узлах конечных элементов.

0 |
|
Рис. 1.1. Распределение (x)
u(x) |
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
u |
(1) |
U2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(2) |
|
U3 |
U4 |
|
|
|
|
|
|
|
u(3) |
u(4) |
U5 |
|
|
|
|
|
|
|
|
||
x |
L(1) |
L(2) |
|
L(3) |
|
L(4) |
x |
|
1 |
(1) 2 |
(2) |
3 |
(3) |
4 |
(4) |
5 |
|
Рис. 1.2. Кусочно-непрерывная |
||||||||
|
|
|
функция и(х) |
|
|
|||
6
u(x) |
|
U i |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
u(k) |
|
U j |
|
|
|
|
|
|||
|
|
|
|
|||
|
|
|
L(k) |
|
|
x |
|
|
i (k) |
j |
|||
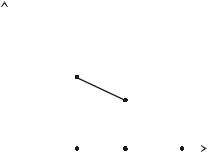
Рис. 1.3. Кусочно-непрерывная функция u(k )
В общем случае при решении задачи методом конечных элементов значения функции U1 , U2 , U3 , … в узлах расчетной сетки
являются искомыми величинами. Для их определения производится построение системы линейных алгебраических уравнений путем минимизации некоторой величины, связанной с физической сущностью задачи, например, с помощью использования метода Галёркина, методов наименьших квадратов или других [1–5].
7

2. ДИСКРЕТИЗАЦИЯ ОБЛАСТИ
При решении задачи МКЭ на первом этапе производится дискретизация исследуемой области, которая включает в себя выбор типа конечного элемента и аппроксимирующего полинома, разбиение на конечные элементы области исследования, нумерацию элементов и узлов [1–5]. Процедуры разбиения двух- и трехмерных областей являются отдельными задачами, от решения которых во многом зависит результат решения поставленной задачи.
2.1. Типы конечных элементов
Размерность решаемой задачи определяет размерность применяемого конечного элемента. Порядок аппроксимирующего полинома зависит от формы и количества узлов конечного элемента.
Если число узлов на единицу больше мерности элемента, то такой конечный элемент называется симплекс-элементом [1–5]. Элементы, содержащие большее количество узлов, называются ком- плекс-элементами. Симплекс-элементы могут быть одномерными, двухмерными и трехмерными (рис. 2.1).
|
|
|
|
|
|
l |
|
|
|
k |
|
|
|
i |
j |
|
j |
i |
|
|
|
|
k |
||||
|
|
i |
|
|
j |
|
|
а |
б |
|
в |
||
Рис. 2.1. Симплекс-элементы: а – одномерный; б – двухмерный (треугольник); в – трехмерный (тетраэдр)
Симплекс-элементам соответствуют линейные полиномы:
– одномерный (рис. 2.1, а)
u 1 2 x ; |
(2.1) |
8

– двухмерный (рис. 2.1, б) |
|
u 1 2 x 3 y ; |
(2.2) |
– трехмерный (рис. 2.1, в) |
|
u 1 2 x 3 y 4 z , |
(2.3) |
где i – коэффициенты полинома ( i 1, 2, 3, ...); x , y , z – коорди-
наты.
Количество коэффициентов аппроксимирующего полинома определяется числом узлов конечного элемента.
Для построения квадратичного аппроксимирующего полинома необходимо наличие трех узлов одномерного конечного элемента
(рис. 2.2, а):
u |
|
x |
x2 , |
(2.4) |
1 |
2 |
3 |
|
|
а для кубического полинома требуется четыре узла конечного элемента (рис. 2.2, б):
|
|
|
u |
|
x |
x2 |
|
x3 . |
(2.5) |
|||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
||
1 |
2 |
3 |
|
1 |
|
2 |
3 |
4 |
||||
|
|
а |
|
|
|
|
|
|
|
б |
|
|
Рис. 2.2. Одномерные конечные элементы высокого порядка: а – квадратичный; б – кубический
Квадратичный треугольный конечный элемент содержит шесть узлов (рис. 2.3), а аппроксимирующий полином – шесть коэффициентов:
u |
|
x |
y |
x2 |
y2 |
xy . |
(2.6) |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Четырехугольный двухмерный конечный элемент является нелинейным с наименьшим числом узлов (рис. 2.4):
u 1 2 x 3 y 4 xy . |
(2.7) |
9

5 |
4 |
4 |
3 |
|
|
||
|
|
|
6 |
3 |
2 |
|
|
|||
|
2 |
||
1 |
|
||
|
1 |
||
|
|
||
Рис. 2.3. Квадратичный |
Рис. 2.4. Четырехугольный |
||
|
треугольный |
||
|
конечный элемент |
||
конечный элемент |
|||
|
|||
2.2. Одномерный симплекс-элемент
Одномерным симплекс-элементом является отрезок с двумя узлами i и j длиной L (рис. 2.5) [1–5]. Значения функции в узлах
равняются Ui и U j .
 u
u
Ui u= 1+ 2x Uj
|
i |
j |
x |
|||
|
Xi |
|
L |
|
||
|
|
|
Xj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5. Одномерный симплекс-элемент |
||||||
Линейный полином u имеет вид |
|
|||||
|
u 1 |
2 x . |
(2.8) |
|||
Здесь x лежит в диапазоне от Xi до X j .
10
