
Lektsia_po_Diskr
.pdf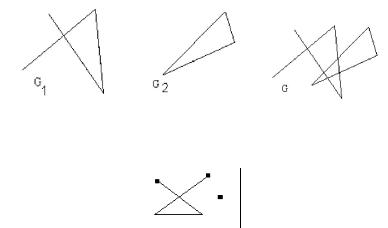
|
|
|
|
|
|
|
|
|
|
63 |
|
|
Метка V : |
|
+ V , r = 6 . |
|
|
|
|
|
|
||||
|
|
4 |
|
3 |
|
4 |
|
|
|
|
|
|
Γ- (V ) = {V |
, V |
. |
Но V |
помечена, а z |
= 0. |
|
|
|||||
|
3 |
|
1 |
5} |
|
1 |
|
|
53 |
|
|
|
Вершина |
V |
помечена и просмотрена. |
|
|
|
|
||||||
|
|
|
|
3 |
|
|
V . |
|
|
|
|
|
Просматриваем вершину |
|
|
|
|
|
|||||||
Γ+ (V ) = {V }. |
|
|
4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
4 |
|
5 |
|
|
|
|
|
|
|
|
Присваиваем вершине V |
метку + V , r = |
min (r , q |
- z ) = min(11, 5 - 5) = 0. Значит, этой вершине метку |
|||||||||
не присваиваем. |
|
|
5 |
4 |
5 |
4 |
45 |
45 |
||||
|
|
|
|
|
|
|
|
|||||
Γ- (V |
4 |
) ={V |
, V |
. Но V |
помечена, а |
z |
= 0. |
|
|
|||
|
|
2 |
3} |
|
3 |
|
24 |
|
|
|
||
Вершина |
V |
помечена и просмотрена. |
|
|
|
|
|
|||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
Дальнейшая расстановка меток невозможна. Значит, полученный поток является оптимальным. Он равен 15.
6.9. Связность в графах
Пусть задан граф G, у которого р – вершин и q – ребер. Если для двух вершин существует цепь, то они называются связными. Граф называется связным, если у него все вершины связны. Если граф может быть задан в виде объединения нескольких подграфов, то каждый такой подграф называется компонентой связности, а количество компонент обозначается буквой k.
Рис. 53. G = G1 U G2, k =2
Рис. 54. Несвязный граф, k=3
Теорема. Пусть имеется три инварианта: р, q и k. Тогда
|
|
p k q |
( p k)( p k 1) |
|
|
|
|
|
|
||
|
|
2 |
|
|
|
Доказательство по индукции: |
. |
|
|
||
|
|
|
|
||
1) Докажем, что |
р – k q |
(1) |
|
||
а). Пусть р = 1; q = 0; тогда k=1 и р – k = 1- 1 = 0 = q ─ верно. |
|
||||
б). Пусть р = 2. |
|
|
|
|
|
При k = 2, получим q = 0 и |
р – k = 0 = q. При k = 1: получим q= 1 и |
р – k = 1 = q. |
|||
Слдовательно, неравенство (1) справедливо.
в). Пусть неравенство (1) справедливо для некоторого р. Покажем, что оно справедливо и для р | = р + 1, то есть мы должны показать, что справедливо р | -k | q | (2) где q | -
количество ребер, получившихся после добавления вершины, а k | - число компонент нового графа. В самом деле:
При р | = р+ 1, k | = k + 1 и q | = q получим р | - k | = р + 1- k - 1 = |
р- k |
(в силу неравенства (1)) q = q | |
. |
|
|
Если же при р | = р + 1 имеем q | = q + n (n 1) и k | = k, то |
р | - k | |
= р+ 1 - k (в силу неравенства (1)) |
|
|
|
|
64 |
q + 1 q+ n= q | . |
|
|
||
Неравенство (2) доказано. |
|
|
||
2) Докажем, что |
( p k )( p k 1) |
q |
(3) |
|
2 |
(1 1)(1 1 1) |
|
||
а). Пусть р = 1; q = 0; k = 1. Тогда |
= 0 = q. |
|||
|
|
|
2 |
|
Пусть неравенство (3) справедливо для некоторого р. Докажем, что оно справедливо и для р | = р + 1, т.е.
|
( p | k | )( p | |
k | 1) |
q | |
(4) |
|
|
2 |
|
|
||
|
|
|
|
|
|
б). Пусть |
р | |
= р + 1; q | |
= q и k | =k + 1. |
(*) |
|
Тогда |
|
|
|
|
|
|
|
( p | k | )( p | k | 1) |
= |
|
|
( p 1 k 1)( p 1 k 1 1) |
= |
||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
в). Пусть р | = р + 1; q | = q + 1 и k | =k. Тогда |
|
|
|
|
|
|
|||||||||||
|
( p | k | )( p| k | 1) |
= |
|
|
( p | k | ) 2 p | k | |
|
= ( подставляя (*) |
||||||||||||
2 |
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и раскрывая скобки) |
= |
|
p 2 |
k 2 2 pk 3( p k ) |
|
2 |
|
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
||
p 2 k 2 2 pk p k |
|
2 |
|
( p k )( p k 1) |
+1 |
||||||||||||||
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||
Что и требовалось доказать.
= |
( p k )( p k 1) |
q = q | |
2 |
|
|
(в силу неравенства (3)) q + 1= q | .
6.10. Циклы
Цепь, в которой начальная и конечная вершины совпадают, называется циклом. Для циклов вводится понятие циклонического числа z = q – р + k.
Если z = 0, то граф не имеет циклов. Если же z = 1, то граф имеет один цикл. Для мультиграфа z выражает число циклов.
Например: при р = 4, q = 8 и k = 1: z= q - р+ k = 8 – 4 + 1= 5.
6.11. Деревья
Если граф не имеет циклов, то он называется ациклическим. В связном графе мостом называется ребро, при удалении которого увеличивается число компонент связности. Если в графе q = р - 1, то граф называется древо-
видным.
Ациклический связный граф называется деревом.
Теорема. Следующие утверждения равносильны, , т.е. если для графа G выполнено любое из условий, то он дерево:
1)Граф ацикличен и связан.
2)Граф ацикличен и древовиден.
3)Граф связан и древовиден.
4)Граф ацикличен, но добавление одного ребра приводит к образованию ровно одного цикла.
5)Каждое ребро графа есть мост.
6)Любые две вершины соединены единственной цепью.
Доказательство:
Из 1 2:
Граф ациклический и связный. Так как граф ацикличен, то z = 0. Так как граф связный, то k = 1. Т.к. z = q - р + k, (1) то 0 = q – р + 1, тогда q = р + 1. А это значит граф древовидный.
Докажем теперь, что из 2 3:
Так как граф древовидный, то q = р - 1. Так как граф ациклический, то z = 0. Подставим в (1): 0 = р - 1- р + k, отсюда k = 1, следовательно, граф связный.
Из 3 4:
Вграфе G: k=1; q = р - 1; из (1) получим z = 0. Добавим ребро и получим граф G | , в котором q | = q + 1; р |
=р и k | = k = 1. Тогда z | = q | - р | + k | = q +1- р+1 = р – 1 + 1- р + 1 =1. z | = 1,следовательно, образовался один цикл.

65
Докажем, что из 4 5:
Допустим, что граф G таков, что некоторое ребро U – не мост, то есть его удаление не приводит к увеличению
компонент связности, а значит, граф G | = G - U остается связным. По 4 он еще и ацикличен. Но если к связному ациклическому графу добавить ребро U, то должен получиться граф с циклом, значит граф циклический. Пришли
кпротиворечию, следовательно, каждое ребро является мостом.
Из 5 6:
Пусть граф G таков, что вершины V i и V j соединены двумя цепями. Так как каждое ребро мост, то удаление
какого-либо ребра из одной цепи должно привести к увеличению компонент связности, то есть V i и V j ─ не
связаны. Но они связаны другой цепью. Пришли к противоречию, следовательно, цепь единственная.
Из 6 1:
Т.к существует цепь, связывающая любые две вершины, то граф связный. Предположим, что граф имеет цикл.
Вершина V i является началом и концом цикла. Тогда V j связана с V i двумя цепями. А это противоречит един-
ственности цепи. |
|
|
|
|
|
|
|
||
Что и требовалось доказать. |
|
|
|
|
|
||||
|
|
|
V1 • |
• V0 |
|
|
|
|
|
|
|
|
|
|
• V2 |
|
|
|
|
|
|
V3• |
|
• V4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V5 • |
|
|
• V6 |
• V7 |
• V8 |
• V9 |
|||
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
V17 |
V18 |
V19 |
Рис. 55. Граф-дерево
В деревьях обычно одну из вершин выделяют и называют корнем.
Вершины, удаленные от корня на одно и то же расстояние образуют ярус. V0- нулевой ярус, V1, V2 – первый ярус, V3, V4, V7, V8, V9 – второй ярус, V5, V6, V15, V16, V17, V18, V19 ─ третий ярус, V10, V11, V12, V13, V14 – четвертый ярус.
Вершины, степень которых равна 1 (висячие) называются концевыми, или листьями. На рис. 55 – это вер-
шины , V10, V11, V12, V13, V14, V15, V16, V17, V18, V19 .
Упорядоченное объединение непересекающихся деревьев называется лесом. Ясно, что лес является несвязным графом.
Остовом связного графа называется подграф, содержащий все его вершины и являющийся деревом. Такое дерево называют покрывающим граф.
Каждая вершина дерева называется узлом.
6.11.1. Задача о минимальном остовном дереве
Эта задача довольно часто возникает на практике при строительстве линий электропередач, каналов связи, газопроводов и т.п.
Задача. Пусть имеется связный взвешенный граф. Веса можно истолковывать как стоимости, расстояния и т.д.
Требуется построить остов с минимальным суммарным весом. (Если граф не связный, то требуется построить минимальный лес).
Существует много способов нахождения какого-нибудь остова данного графа. Например, алгоритм поиска в глубину строит остов по ребрам возврата, но этот остов может не быть кратчайшим.
V1 |
|
1 |
V2 |
V1 |
1 |
V2 |
||||
|
|
• |
|
|
• |
• |
|
|
• |
|
|
|
|
|
|
||||||
4 |
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
|
• |
|
|
• |
• |
|
• |
||
|
|
|
|
|
|
|
|
|
|
|
V4 |
1 |
|
V3 |
V4 |
|
V3 |
||||

|
|
|
|
|
66 |
|
Рис. 56. Граф |
|
Рис. 57. Дерево кратчайших путей |
|
|||
V1 |
1 |
V2 |
|
V1 |
1 |
V2 |
• |
|
• |
|
• |
|
• |
|
|
2 |
|
|
2 |
|
• |
1 |
• |
• |
|
|
• |
V4 |
V3 |
V4 |
|
1 |
V3 |
|
Рис. 58. Два кратчайших остова
6.11.2. Жадный алгоритм Краскала построения
кратчайшего остова
Пусть задан связный граф, имеющий р вершин и с различными длинами своих ребер. На первом шаге находим ребро наименьшей длины и помещаем его в будущий остов. Получили подграф. Затем из оставшихся ребер находим второе ребро наименьшей длины и помещаем его в подграф ─ будущий остов. Затем из оставшихся ребер находим ребро наименьшей длины, не образующее цикла с ранее выбранными ребрами, и помещаем его в подграф. Продолжаем этот процесс до тех пор, пока есть ребра, не образующие цикл в подграфе. Т.к. граф связный, то в подграф попадут все вершины, т.е. подграф будет содержать р вершин. Следовательно, полученный в конечном итоге подграф будет остовным. Т.к. он ацикличен, то он дерево. А т.к. в него включались ребра наименьшей длины, то оно и будет искомым остовом.
Замечание. Поиск наименьшего ребра существенно упрощается, если упорядочить длины ребер по возрастанию.
6.11.3. Ориентированные деревья
Орграф называется ориентированным деревом (ордеревом), если
1.существует единственный узел, полустепень захода которого равна 0 (корень),
2.полустепень захода остальных узлов равна 1,
3.все узлы достижимы из корня.
Пример.
• |
|
• |
|
• |
|
• |
• |
• |
• |
• |
• |
• |
• |
• |
|
• |
|
|
|
• |
|
|
|
|
|
|
• |
|
• |
|
|
|
|
|
Рис. 59. Ордеревья с 4 узлами
Остальные ордеревья с 4 узлами изоморфны графам на рис. 59. Теорема. Свойства ордеревьев.
1.Если q – число дуг, а p – число узлов оррдерева, то q = p - 1.
2.Если в оррдереве отменить ориентацию ребер, то получится свободное дерево.
3.В оррдереве нет контуров.
4.Для каждого узла существует единственный путь из корня.
5.Если в свободном дереве любую вершину назначить корнем, то получится оррдерево.
Доказательство.
1. Т.к. в каждый узел, кроме корня, заходит единственная дуга (п. 1, 2 определения), то q = p - 1
67
2.Отмена ориентации в оррдереве приведет к созданию связного дерева (иначе нарушается п.3 определения). Из доказанного свойства 1 следует, что этот граф древовиден. Граф связен и древовиден, значит, он – дерево.
3.Если допустить в ордереве наличие контуров, то при отмене ориентации получится граф с циклами, т.е. не дерево, что противоречит свойству 2.
4.Если предположить наличие двух путей для некоторого узла, то при отмене ориентации получится граф
сциклами, т.е. не дерево, что противоречит свойству 2.
5.Пусть вершина u назначена корнем. Инцидентные с ней ребра ориентируем в глубину. Т.к. для любой
вершины v существует единственная цепь, соединяющая u и v , то полустепень захода d+(v) = 1 v, и каждый узел достижим из корня.
6.11.4. Упорядоченные деревья
Если в качестве корня в ордереве выбрать какой-нибудь узел v, то множество узлов, достижимых из v образует орграф с корнем v (поддерево).
Если относительный порядок поддеревьев установлен, то ордерево называется упорядоченным.
Ордеревья и упорядоченные деревья часто используются в программировании. Например, для представления выражений, вложенных блоков, для представления иерархической структуры операторов, структуры вложенности каталогов и файлов, скобочные структуры и т.д. Существует договоренность об изображении корня вверху дерева, направление дуг сверху вниз, что позволяет не рисовать стрелок, если это не приводит к путанице.
Если рассматривать деревья рис. 59 как упорядоченные деревья, то они все различные. Если рассматривать их как ордеревья, то I = П, но П ≠ Ш. Если рассматривать их как свободные деревья, то они все изоморфны.
6.11.5..Бинарные деревья
В информатике широко используются подмножества множества деревьев, в которых каждый узел является либо листом, либо образует два поддерева – левое и правое. Такой вид деревьев называется бинарным деревом. Бинарное дерево не является упорядоченным ордеревом.
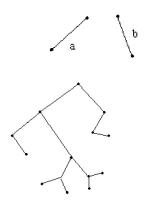
Например, деревья а и b различны.
Рис. 60. Пример бинарного дерева
Бинарное дерево называется полным уровня п, если каждый узел уровня п является листом, а каждый узел меньшего уровня имеет непустые левое и правое поддеревья.
Примером полного дерева может служить таблица розыгрыша кубка по какому-нибудь виду спорта по олимпийской системе (плей офф).
6.12. Эйлеровы циклы
Задача о Кёнигсбергских мостах.
По Кёнигсбергу протекает река Прегель, образующая два острова, связанных между собой и с берегами семью мостами. Надо разработать такой замкнутый маршрут, в котором каждый из мостов проходится один раз.

68
Рис. 61. Задача о Кёнигсбергских мостах
Эта задача была решена Эйлером в 1736 г.
Задача сводится к построению циклического графа с 4 вершинами и 7 ребрами так, чтобы каждое ребро входило в него по одному разу.
Аналогична задача о рисовании конвертов, не отрывая карандаша и не рисуя дважды одну линию.
Рис.62. Закрытый и открытый конверты
Если граф имеет цепь (цикл), соединяющую две вершины и содержащую все ребра графа по одному разу,
то цепь (цикл) называется эйлеровой, а сам граф называется эйлеровым. Теорема.
Для того чтобы граф бы эйлеровым, необходимо и достаточно, чтобы число вершин, степень которых нечетна, равнялось 0 или 2.
Доказательство: Необходимость:
Пусть граф эйлеров, то есть существует или эйлерова цепь, или эйлеров цикл. И пусть имеется одна вершина с нечетной степенью, не являющаяся ни начальной, ни конечной, степень которой равна 2п +1. Тогда 2п +1 - е ребро приведет нас в эту вершину п + 1-й раз, и покинуть её мы не сможем. Следовательно, такими вершинами могут быть только начальная и конечная. Их две в случае наличия цепи и 0 в случае цикла.
А |
|
|
|
В |
|
|
|
||
|
|
|
Рис.63. Начальная и конечная точка цепи
Достаточность
Пусть имеется две вершины с нечетной степенью. Выйдя из вершины А, мы попадем в вершины, из которых всегда можно выйти. Таким образом, все ребра, инцидентные вершинам с четной степенью, будут пройдены, и мы придем к вершине В. Мы можем выйти, затем войти, но опять выйти уже не сможем. Таким образом, между А и В существует эйлерова цепь.
Докажем существование эйлерова цикла для вершины А:
Пусть эйлеров цикл существует для некоторых q1 ребер. Докажем, что он существует для q > q1 . Так как
для любого q1 <q существует эйлеров цикл, а каждая вершина имеет четную степень, то существует вершина,
принадлежащая обоим циклам (уже пройденному и еще нет, ребра которого не входят в 1 - ый цикл). Объединяя эти циклы, получим эйлеров цикл.

69
Рис.64. Образование эйлеровоого цикла
Таким образом, из теоремы Эйлера следует, что задача о Кёнигсбергских мостах и о рисовании закрытого конверта решений не имеют, т.к. вершин нечетной степени больше двух. Задача об открытом конверте решение имеет. Построение его следует начинать из вершины нечетной степени.
6.13.Гамильтоновы графы
Всредине 19 века ирландский математик Уильям Гамильтон опубликовал задачу о «кругосветном путешествии». Требуется обойти все вершины графа (столицы государств) по одному разу и вернуться в исходную вершину.
.
Рис. 65. Задача о «кругосветном путешествии» Если граф имеет простой цикл, содержащий все вершины графа, то этот цикл называется гамильтоновым
циклом, а сам граф называется гамильтоновым графом.
Гамильтонов цикл не обязательно содержит все ребра графа. Совершенно очевидно, что гамильтоновы графы являются связными.
Решение задачи о «кругосветном путешествии».
Находясь в любой вершине, мы можем повернуть вправо (П) или влево (Л). Условимся вместо ПП писать П 2 и т.д. Тогда решение может быть задано формулой
(Л3 П3 (ЛП)2)2 = ЛЛЛ ППП ЛП ЛП ЛЛЛ ППП ЛП ЛП.
Решение не единственно. Можно начинать в обратном порядке. Можно сделать круговую перестановку.
6.13.1. Существование гамильтоновых графов
Лемма. Любой граф G можно превратить в гамильтонов, добавив достаточное количество вершин и ребер.
Доказательство.
К вершинам v1, v2, …, vр добавим вершины u1, u2, …, uр и множество ребер {( v i ,u i)}U {( u I ,vi+11)}. Получим
гамильтонов граф. |
|
Теорема Дирака. Если в графе G степень каждой вершины |
d(v) ≥ р/2 (р ─ число вершин), то этот граф |
является гамильтоновым. |
|
Доказательство от противного. |
|
Предположим, что граф не гамильтонов. Добавим к нему наименьшее количество п вершин uI, соединяя их со всеми вершинами v так, чтобы получился гамильтонов граф.
Пусть v, u1, w, …, v – гамильтонов цикл в новом графе. G1, причем v G, u1 G1, u1 G. Такая пара вершин v и u1 в гамильтоновом цикле обязательно найдется, иначе граф G был бы гамильтоновым. Тогда w G и w {u i}, иначе вершина u1 была бы не нужна. Вершина u1 была бы не нужна, если бы вершины v и w были бы смежными.
Если в цикле v, u1, w, …, х, у, …, v есть вершина у, смежная с вершиной w, то вершина х несмежна с вершиной v, т.к. иначе можно было бы построить гамильтонов цикл v, х, w, у, …, v без u1. Отсюда следует, что число вершин
70
графа G1, не смежных с v, не менее числа вершин смежных с w. Но для любой вершины w графа G имеем d(w) ≥ р/2 + п по построению и d(v) ≥ р/2 + п. Общее число вершин, смежных и несмежных с v, равно р + п -1. Получим
Р + п -1 ≥ d(w) + d(v) ≥ р/2 + п+ р/2 + п = р + 2п.
Итак , р+ п -1 ≥ р + 2п. Отсюда 0 ≥ п + 1, что противоречит положительности п.
6.13.2. Задача коммивояжера
Имеется р городов, связанных между собой дорогами с известными их длинами. Требуется обойти все города по одному разу так, чтобы сумма пройденных расстояний была наименьшей.
Решение может быть осуществлено методом прямого перебора, что потребует рассмотрения р! вариантов с последующим выбором оптимального. Даже для небольших р это весьма затруднительно.
Данная задача относится к числу, так называемых, NP - задач, для которых не известен эффективный алгоритм, существенно сокращающий перебор вариантов.
Библиографический список
1.Акимов О.Е. Дискретная математика. – М., Лаборатория Базовых Знаний, 2003.
2.Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.,изд. МГТУ им. Н.Э. Баумана, 20004
3.Березина Л.Ю. Графы и их применение. – М.: Просвещение, 1979.
4.Берж К. Теория графов и ее применения. – М.: ИЛ, 1962.
5.Булос ДЖ., Джеффри Р. Вычислимость и логика. М.; Мир, 1994.
6.Виленкин Н. Я. Комбинаторика. М.; Наука, 1969.
7.Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: Наука, 1992.
8.Гиндикин С.Г. Алгебра логики в задачах. – М.: Наука, 1972.
9.Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1987.
10.Грэхем Р., Кнут Д, Поташник О. Конкретная математика. Основание информатики. М. – Мир, 1998.
11.Евстигнеев В.А. Применение теории графов в программировании. – М.: Наука, 1985.
12.Зыков А.А. Основы теории графов. – М.: Наука, 1987.
13.Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергия, 1980.
14.Линский В. Комбинаторика для программистов. – М.: Мир, 1988.
15.Ломазова И. А. Дискретная математика. Математические основы обработки информации. Учеб. пособие.- ЯГУ. Ярославль, 2000.
16.Мелехов А.Н. Ориентированные графы и конечные автоматы. – М.: Наука, 1971.
17.Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Изд-во МАИ, 1992.
18.Никольская И.Л. Математическая логика. – М.: Высшая школа, 1981.
19.Новиков Ф. А. Дискретная математика. – С-Пб.: Питер, 2001.
20.Спирина М.С., Спирин П.А. Дискретная математика. – М., ACADEMA, 2004.
21.Трахтенброт Евстигнеев В.А. Применение теории графов в программировании. – М.: Наука, 1985.
22.Яблонский С.В. Введеие в дискретную математику. 3-е изд. – М., Высш. Шк., 2001.
ОГЛАВЛЕНИЕ
Предисловие………………………………………………………………..3
1.Основные понятия………………………………………………………3
2.Множества…………...……………………………………………….3
2.1. Подмножества .................................................................................. |
4 |
2.2. Равенство множеств......................................................................... |
4 |
2.3. Мощность множеств........................................................................ |
4 |
2.4. Алгебра множеств. Операции над множествами. ......................... |
4 |
2.5. Свойства операций........................................................................... |
5 |
2.6. Разбиение множества на классы..................................................... |
6 |
2.7. Декартово произведение множеств................................................ |
7 |
2.7.1. Декартова степень .................................................................... |
8 |
2.7.2. Декартово произведение n множеств ..................................... |
8 |
2.7.3. Свойства декартового произведения...................................... |
8 |
2.8. Отношения....................................................................................... |
8 |
2.8.1 Композиция отношений............................................................ |
9 |
2.8.2. Отношения на множестве........................................................ |
9 |
2.8.3. Виды отношений ...................................................................... |
9 |
2.9. Функции.......................................................................................... |
10 |
71
2.9.1. Представление функций в ЭВМ ........................................... |
10 |
3.Комбинаторика……………...……………………………………...11
3.1. Размещения.................................................................................... |
11 |
3.1.1. Формула числа размещений без повторений....................... |
11 |
3.1.2. Другой вид формулы числа размещений ............................. |
12 |
3.2. Перестановки.................................................................................. |
12 |
3.3. Сочетания ....................................................................................... |
12 |
3.3.1. Свойства сочетаний ............................................................... |
13 |
3.4. Размещения с повторениями......................................................... |
13 |
3.4.1. Число подмножеств данного множества.............................. |
14 |
3.5. Перестановки с повторениями...................................................... |
14 |
3.6. Сочетания с повторениями ........................................................... |
14 |
4. Основы математической логики…………….………………………...15 |
|
4.1. Высказывания................................................................................. |
15 |
4.2. Основные операции над высказываниями................................... |
15 |
4.3. Формулы ......................................................................................... |
18 |
4.3.1. Соглашение о скобках ........................................................... |
18 |
4.3.2. Булевы функции ..................................................................... |
18 |
4.3.3 Равносильные формулы.......................................................... |
18 |
4.3.4. Основные равносильности .................................................... |
18 |
4.4. Решение логических уравнений ................................................... |
19 |
4.5. Виды формул.................................................................................. |
20 |
4.5.1. Связь равносильности и эквиваленции ............................... |
20 |
4.6. Нормальные формы ....................................................................... |
21 |
4.6.1. Дизъюнктивная нормальная форма формулы ..................... |
21 |
4.6.2. Конъюнктивная нормальная форма...................................... |
21 |
4.6.3. Методы доказательства тавтологии...................................... |
21 |
4.6.4. Совершенные нормальные формы ....................................... |
22 |
4.7. Решение логических задач ............................................................ |
24 |
4.8. Анализ рассуждений...................................................................... |
24 |
4.8.1. Правила вывода ...................................................................... |
25 |
4.8.2. Вывод ...................................................................................... |
26 |
4.8.3. Теорема дедукции .................................................................. |
27 |
4.9. Предикаты ...................................................................................... |
27 |
4.9.1 Область истинности ................................................................ |
28 |
4.9.2. Операции над предикатами ................................................... |
28 |
4.9.3. Кванторы................................................................................. |
29 |
4.9.4. Операции с кванторами ......................................................... |
29 |
4.9.5. Формулы ................................................................................. |
30 |
4.9.6. Равносильность....................................................................... |
30 |
4.9.7. Равносильности с кванторами.............................................. |
30 |
4.9.8. Запись математических предложений с помощью предикатов 31 |
|
4.9.9. Общезначимые формулы....................................................... |
31 |
4.9.10. Некоторые общезначимые формулы с кванторами .......... |
32 |
4.9.11. Рассуждения.......................................................................... |
33 |
4.9.12. Вывод .................................................................................... |
33 |
5. Кодирование информации……....……….…………………………….34 |
|
5.1. Задача кодирования ....................................................................... |
34 |
5.2. Равномерное кодирование............................................................. |
35 |
5.3. Алфавитное кодирование.............................................................. |
35 |
5.4. Кодирование с минимальной избыточностью........................... |
35 |
5.5. Префиксное кодирование.............................................................. |
36 |
5.6. Неравенство Макмиллана ............................................................. |
36 |
5.7. Понятие вероятности ..................................................................... |
37 |
5.8. Цена кодирования .......................................................................... |
37 |
5.9. Алгоритм Фано префиксного кодирования................................. |
37 |
5.10. Оптимальное кодирование.......................................................... |
39 |
5.10.1. Теорема об оптимальном кодировании.............................. |
40 |
5.10.2. Алгоритм Хаффмена............................................................ |
41 |
5.11. Помехоустойчивое кодирование ................................................ |
42 |
61.1. Смежность................................................................................ |
43 |
6.1.2. Виды графов ........................................................................... |
43 |
6.1.3. Изоморфизм............................................................................ |
44 |
|
72 |
6.1.4. Инварианты............................................................................. |
45 |
6.2. Подграфы........................................................................................ |
45 |
6.3. Маршруты. Цепи. Циклы .............................................................. |
45 |
6.3.1. Расстояние............................................................................... |
46 |
6.3.2. Связность ................................................................................ |
46 |
6.4. Задание графа ................................................................................. |
47 |
6.5. Метод математической индукции ............................................... |
49 |
6.6.1. Задача о наименьшем числе аварий...................................... |
50 |
6.7. Взвешенный граф........................................................................... |
52 |
6.7.1. Задача о кратчайшем пути..................................................... |
52 |
6.7.2. Алгоритм Форда..................................................................... |
52 |
6.8. Задача о максимальном потоке..................................................... |
54 |
6.8.1. Теорема Форда – Фолкерсона ............................................... |
55 |
6.9. Связность в графах ........................................................................ |
63 |
6.10. Циклы............................................................................................ |
64 |
6.11. Деревья.......................................................................................... |
64 |
6.11.1. Задача о минимальном остовном дереве............................ |
65 |
6.11.2. Жадный алгоритм Краскала построения............................ |
66 |
6.11.3. Ориентированные деревья................................................... |
66 |
6.11.4. Упорядоченные деревья ...................................................... |
67 |
6.11.5..Бинарные деревья................................................................. |
67 |
6.12. Эйлеровы циклы........................................................................... |
67 |
6.13. Гамильтоновы графы................................................................... |
69 |
6.13.1. Существование гамильтоновых графов ............................. |
69 |
6.13.2. Задача коммивояжера .......................................................... |
70 |
Библиографический список……………….…………………………….70 |
|
