
А5 Главы 1-4
.pdf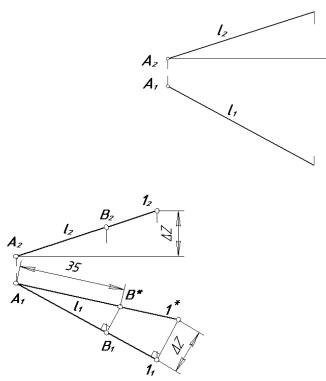
Задача 6
От точки А є l отложить на прямой l отрезок AВ длиной
35 мм.
Решение: Алгоритм:
– на прямой l отметить произвольную точку 1;
– определить н.в. отрезка 1А методом прямоугольного треугольника;
– на н.в. А11* отложить 35 мм и отметить точку В*;
– построить точки В1 и В2.
3.5. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ
С ПОМОЩЬЮ КОНКУРИРУЮЩИХ ТОЧЕК
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай:
1. Параллельные прямые.
Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллель-
43
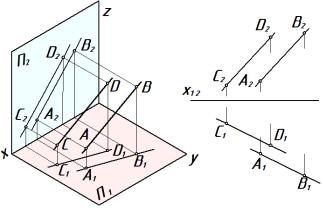
ных прямых на любую плоскость (не перпендикулярную данным прямым) параллельны. Это свойство параллельного проецирования остается справедливым и для ортогональных проек-
ций, то есть если AB CD, то A1B1 C1D1; A2B2 C2D2; A3B3 C3D3
(рис.3.3). В общем случае справедливо и обратное утверждение.
а) б) Рис. 3.3. Параллельные прямые: а – модель; б – эпюр
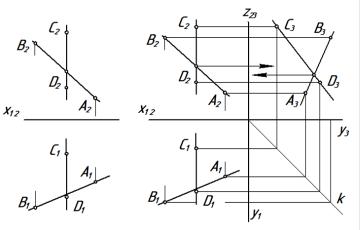
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны A1B1 C1D1; A2B2 C2D2 (рис.3.4,а), но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 3.4, б).
В рассмотренном случае проекции отрезков на плоскость П3 пересекаются A3B3∩C3D3, следовательно, они не параллельны.
2. Пересекающиеся прямые.
Пересекающимися называются две прямые, лежащие в одной плоскости и имеющие одну общую точку. Если прямые пересекаются, то точки пересечения их одноименных проекций находятся на одной линии связи (рис. 3.5).
44

а) б)
Рис. 3.4. Взаимное расположение прямых: а – двухкартинный чертеж; б – трехкартинный чертеж
а) б)
Рис. 3.5. Пересекающиеся прямые: а – модель; б – эпюр
В общем случае справедливо и обратное утверждение, но есть два частных случая:
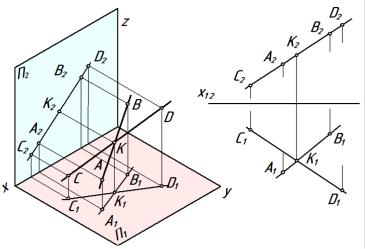
1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например профильной плоскости проекций
45
(рис. 3.6), по двум проекциям невозможно судить об их взаимном расположении. Так, горизонтальная и фронтальная проекции отрезков АВ и СD пересекаются и точка пересечения проекций лежит на одной линии связи, профильные проекции этих отрезков тоже пересекаются, однако точка их пересечения не лежит на одной линии связи с точками пересечения горизонтальной и фронтальной проекций отрезков, следовательно, не пересекаются и сами отрезки.
а) б)
Рис. 3.6. Взаимное расположение прямых: а – двухкартинный чертеж; б – трехкартинный чертеж
2. Пересекающие прямые расположены в одной плоскости, например, перпендикулярной к фронтальной плоскости проекций (рис. 3.7). О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной проекции, например по проекции на горизонтальную плоскость проекций
(А1В1∩С1D1 АВ∩СD).
3. Скрещивающиеся прямые.
Скрещивающимися называются две прямые не лежащие в одной плоскости. Если прямые не пересекаются и не параллельны между собой, то точки пересечения их одноименных проекций (если они есть) не лежат на одной линии связи.
46
а) б)
Рис. 3.7. Пересекающиеся прямые: а – модель; б – эпюр
Для определения видимости прямых относительно плоскостей проекции используются конкурирующие точки.
Рассмотрим комплексный чертеж скрещивающихся прямых а и b (рис. 3.8). Определим, какая из прямых расположена выше другой (относительно плоскости П1) или ближе другой к наблюдателю (относительно плоскости П2). Для этого необходимо проанализировать положение конкурирующих точек А и В, С и D, принадлежащих этим прямым. В данном случае точки А и В – фронтально-конкурирующие, а точки С и D – горизон- тально-конкурирующие.
Определим видимость на плоскости проекций П2. Из двух конкурирующих точек В и А, принадлежащих скрещивающимся прямым а и b, видимой на плоскости П2 будет точка В, так как В1 расположена ближе к наблюдателю, что видно при взгляде спереди по указанной стрелке. Точка А1 дальше от наблюдателя, следовательно, точка А будет не видима на плоскости П2 (А2 обозначена второй в совпадающих проекциях).
Определим видимость на плоскости проекций П1. Из рис. 3.8 следует, что при взгляде сверху по указанной стрелке D2
47

выше С2 относительно П1. Следовательно, точка D, принадлежащая прямой а, будет видима, а точка С, принадлежащая прямой b, будет не видима (D1 обозначена второй в совпадающих проекциях).
Понятие конкурирующих точек используется в решении позиционных задач, когда требуется определить видимость.
а) б)
Рис. 3.8. Скрещивающиеся прямые: а – модель; б – эпюр
Рассмотрим решение задач по изучаемой теме.
Задача 1
Определить взаимное положение прямых.
Решение:
Прямые c и d , m и n параллельны, так как c 1 || d1 , c2 || d2 и n1 || m1 , n2 || m2 .
48
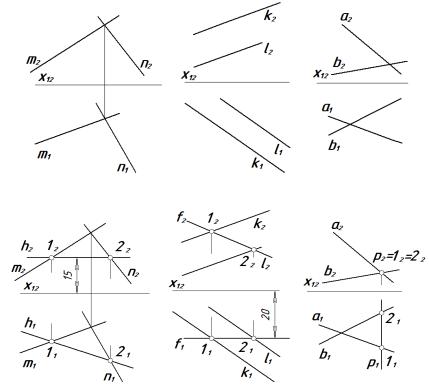
Прямые k и l , t и u пересекаются, так как точки пересечения одноименных проекций принадлежат одной линии связи.
Прямые a и b , p и q скрещиваются, так как отсутствуют признаки параллельности и пересечения.
Задача 2
Пересечь прямые:
а) m и n горизонталью с высотой 15 мм; б) k и l фронталью с глубиной 20 мм;
в) а и b фронтально-проецирующей прямой.
а) |
б) |
в) |
Решение:
а) |
б) |
в) |
49
Задача 3
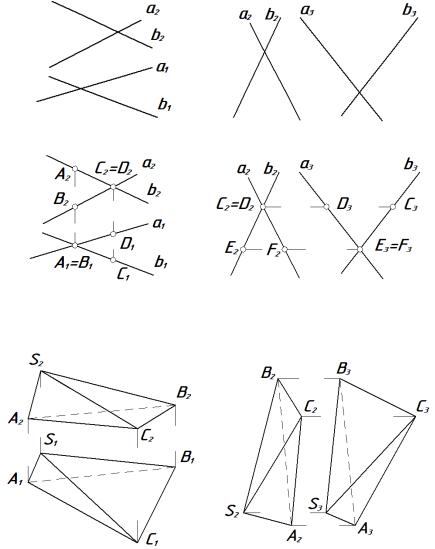
Определить конкурирующие точки на прямых а и b:
а) фронтально- и горизонтально- |
б) фронтально- и профильно- |
конкурирующие точки |
конкурирующие точки |
Решение:
|
Задача 4 |
Обвести ребра SC и AB пирамиды SAВC с учетом их ви- |
|
димости: а) на П1 и П2 |
б) на П2 и П3 |
50
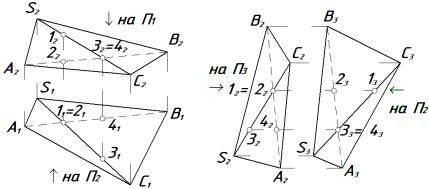
Решение:
3.6. ТЕОРЕМА О ПРОЕЦИРОВАНИИ ПРЯМОГО УГЛА. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Угол геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Углом между прямыми называется меньший из двух углов между лучами, параллельными этим прямым. Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и еѐ проекцией на данную плоскость.
Рассмотрим ряд свойств ортогональных проекций плоских углов:
1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (теорема о проецировании прямого угла).
Дано: АВС 90о; ВС // П1; АС П1. Доказательство теоремы:
– продлим отрезок АС до пересечения с плоскостью П1
(рис. 3.9);
–получим горизонтальный след прямой – точку М = М1, одновременно принадлежащую прямой и ее проекции. Из свойства ортогонального проецирования следует, что ВС // В1С1;
51
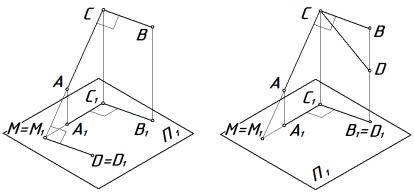
– через точку М проведем прямую МD параллельно С1В1, она будет параллельна и СВ, а следовательно, СМD 90о.
Согласно теореме о трех перпендикулярах, С1МD 90о. Таким образом, MD А1С1 и MD // В1С1, следовательно,А1С1В1= 90о, что и требовалось доказать.
В случае, когда АС П1, проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.
2. Если проекция угла представляет угол 900, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 3.10).
Рис. 3.9. Теорема о |
Рис. 3.10. Обратная теорема о |
проецировании прямого угла |
проецировании прямого угла |
3.Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.
4.Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.
52
