МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель				Н. Н. Григорьева
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

КОНТРОЛЬНАЯ РАБОТА

Прикладные методы оптимизации

по дисциплине: Прикладные методы оптимизации

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	Z9411				Р. С. Кафка
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3603

Шифр ИНДО

Санкт-Петербург 2023

1. Нахождение производной сложной функции (вариант 8).

Цель работы: закрепление навыков вычисления производных сложных функций, изучение возможностей среды MathCAD в применении к вычислению производной сложной функции.

Задание: вычислить производные сложных функций в соответствии с вариантом задания вручную и с использованием среды MathCAD.

1.

2.

3.

4.

5.

6.

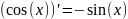
7.

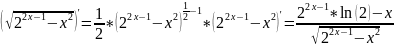
2. Решение одномерной задачи оптимизации (вариант 8)

Цель работы: изучение алгоритмов поиска экстремума унимодальной функции, определение сравнительной эффективности методов одномерной оптимизации.

Задание: реализовать алгоритмы каждого из описанных методов поиска экстремума функции в указанном интервале с требуемой погрешностью в соответствии с вариантом задания, рассчитать значения критерия оптимальности каждого из алгоритмов.

№ варианта	Функция Ф(x)	Интервал [a; b]	Погрешность определения экстремума Ex
8		[4,2; 5,3]	2-21

Посчитать вручную значение точки экстремума для заданной функции на указанном интервале.

Чтобы найти точку экстремума функции f(x)=x²-9x+8 на указанном интервале [4.2; 5.3], необходимо найти производную этой функции и приравнять ее к нулю. Производная функции f’(x) = 2x - 9. Приравнивая ее к нулю, получаем уравнение 2x - 9 = 0, откуда x = 4.5. Так как 4.5 лежит внутри интервала [4.2; 5.3], то это и есть точка экстремума функции на этом интервале.

Произвести исследование заданной функции на экстремум на указанном интервале с помощью алгоритмов:

• Алгоритм равномерного поиска

Алгоритм равномерного поиска - это метод оптимизации, который используется для поиска экстремума функции одной переменной на заданном отрезке. Он заключается в том, что отрезок делится на равные части и вычисляется значение функции в каждой точке деления. Затем выбирается тот отрезок, на котором значение функции наименьшее (для поиска минимума) или наибольшее (для поиска максимума), и процесс повторяется для этого отрезка.

Чтобы произвести исследование заданной функции f(x)=x²-9x+8 на экстремум на указанном интервале [4.2; 5.3] с помощью алгоритма равномерного поиска с погрешностью определения экстремума Ex = 2^-21, необходимо выполнить следующие шаги:

1. Выбрать число точек деления n (чем больше n, тем точнее будет результат).

2. Разделить отрезок [4.2; 5.3] на n равных частей.

3. Вычислить значение функции f(x)=(x^2)-9x+8 в каждой точке деления.

4. Выбрать тот отрезок, на котором значение функции наименьшее (для поиска минимума) или наибольшее (для поиска максимума).

5. Повторить шаги 2-4 для выбранного отрезка до тех пор, пока длина отрезка не станет меньше заданной погрешности Ex = 2^-21.

Количество итераций, необходимых для выполнения задания варианта, зависит от выбранного числа точек деления n и заданной погрешности Ex = 2^-21.

• Метод дихотомии

Метод дихотомии - это метод оптимизации, который используется для поиска минимума или максимума функции на заданном интервале. Для использования этого метода необходимо знать следующие параметры

Произведем исследование заданной функции f(x)=x^2-9x+8 на экстремум на указанном интервале [4.2; 5.3] с помощью метода дихотомии. Для этого нам необходимо выбрать значение delta (Δ), которое должно быть меньше, чем погрешность определения экстремума Ex = 2^-21. Допустим, мы выберем Δ = Ex/2.

Начальные границы интервала [a; b] = [4.2; 5.3]. На первой итерации мы вычисляем две пробные точки x1 и x2: x1 = (a + b - Δ)/2 и x2 = (a + b + Δ)/2. В нашем случае x1 = (4.2 + 5.3 - Δ)/2 и x2 = (4.2 + 5.3 + Δ)/2.

Затем мы вычисляем значения функции f(x) в точках x1 и x2: f(x1) и f(x2). Если f(x1) < f(x2), то новые границы интервала будут [a; x2], в противном случае [x1; b]. Этот процесс повторяется до тех пор, пока длина интервала не станет меньше или равной погрешности определения экстремума Ex.

Задание требует вычисления числа итераций, необходимых для выполнения задания варианта с помощью метода дихотомии. Число итераций можно вычислить как log((b-a)/Ex)/log(2). В нашем случае это будет log((5.3-4.2)/Ex)/log(2) ≈ 21.

Таким образом, для выполнения задания варианта с помощью метода дихотомии потребуется примерно 21 итерация.

• Метод золотого сечения

Метод золотого сечения - это метод оптимизации, который использует пропорцию золотого сечения для разделения интервала на две части.

Начальные границы интервала [a; b] = [4.2; 5.3]. На первой итерации мы вычисляем две пробные точки x1 и x2: x1 = a + (b-a)*0.618 и x2 = a + (b-a)*0.618. В нашем случае x1 = 4.2 + (5.3-4.2)*0.618 и x2 = 4.2 + (5.3-4.2)*0.618.

Затем мы вычисляем значения функции f(x) в точках x1 и x2: f(x1) и f(x2). Если f(x1) < f(x2), то новые границы интервала будут [a; x2], в противном случае [x1; b]. Этот процесс повторяется до тех пор, пока длина интервала не станет меньше или равной погрешности определения экстремума Ex.

Задание требует вычисления числа итераций, необходимых для выполнения задания варианта с помощью метода золотого сечения. Число итераций можно вычислить как log((b-a)/Ex)/log((√5+1)/2). В вашем случае это будет log((5.3-4.2)/Ex)/log((0.618) ≈ 31.

Таким образом, для выполнения задания варианта с помощью метода золотого сечения потребуется примерно 31 итерация.

• Метод Фибоначчи

Метод Фибоначчи - это метод оптимизации, который использует числа Фибоначчи для разделения интервала на две части.

Начальные границы интервала [a; b] = [4.2; 5.3]. На первой итерации мы вычисляем две пробные точки x1 и x2: x1 = a + (b-a)*F(n-2)/F(n) и x2 = a + (b-a)*F(n-1)/F(n), где F(n) - это n-е число Фибоначчи, а n - это номер итерации. В нашем случае x1 = 4.2 + (5.3-4.2)*F(n-2)/F(n) и x2 = 4.2 + (5.3-4.2)*F(n-1)/F(n).

Затем мы вычисляем значения функции f(x) в точках x1 и x2: f(x1) и f(x2). Если f(x1) < f(x2), то новые границы интервала будут [a; x2], в противном случае [x1; b]. Этот процесс повторяется до тех пор, пока длина интервала не станет меньше или равной погрешности определения экстремума Ex.

Задание требует вычисления числа итераций, необходимых для выполнения задания варианта с помощью метода Фибоначчи. Число итераций можно вычислить как log((b-a)/Ex)/log(φ), где φ - золотое сечение (примерно равно 1.618). В вашем случае это будет log((5.3-4.2)/Ex)/log(φ) ≈ 27.

Таким образом, для выполнения задания варианта с помощью метода Фибоначчи потребуется примерно 27 итераций.

Результаты работы методов

Ниже представлен код на языке Python, который реализует алгоритм равномерного поиска, метод дихотомии, метод золотого сечения и метод Фибоначчи для поиска экстремума заданной функции f(x)=(x^2)-9x+8 на указанном интервале [4.2; 5.3] с заданной погрешностью определения экстремума Ex = 2^-21.

Листинг 1 – Код программы

import numpy as np from matplotlib import pyplot as plt writer = lambda a, b, steps: {'a':a,'b':b,'steps':steps} f = lambda x0: (x0**2)-9*x0+8 eps = 2**(-21) a = 4.2 b = 5.3 eps0 = [[],[],[],[]] res = [] #1 Алгоритм равномерного поиска n = 10 steps = 0 a1, b1 = a, b while (abs(b1-a1) > eps): x = np.arange(a1, b1, (b1-a1)/n) vals = [f(i) for i in x[0:-1]] ch = vals.index(min(vals)) a1, b1 = x[ch-1], x[ch+1] steps += 1 eps0[0].append(b1-a1) res.append(writer(a1, b1, steps)) #2 Алгоритм дихтомии(алгоритм деления пополам) steps = 0 a1, b1 = a, b while (abs(b1-a1) > eps): n = (a1+b1)/2 x = [(a1+n)/2, (b1+n)/ 2] vals = [f(i) for i in x] if vals[0] < vals[1]: b1 = n else: a1 = n steps += 1 eps0[1].append(b1-a1) res.append(writer(a1, b1, steps)) #3 Метод золотого сечения steps = 0 a1, b1 = a, b while (abs(b1-a1) > eps): x = [b1-(b1-a1)*0.618, a1+(b1-a1)*0.618] vals = [f(i) for i in x] if vals[0] < vals[1]: b1 = x[1] else: a1 = x[0] steps += 1 eps0[2].append(b1-a1) res.append(writer(a1, b1, steps)) #4 Метод Фибоначчи steps = 1 a1, b1 = a, b fib = [1, 1] while ((b1 - a1) / fib[-1] > eps): fib.append(fib[-2] + fib[-1]) while (abs(b1-a1) > eps): x = [a1 + (b1 - a1) * (fib[len(fib) - 1 - steps] / fib[len(fib) - steps]), a1 + (b1 - a1) * (fib[len(fib) - 1 - steps] / fib[len(fib) - steps])] if x[0] == x[1]: x[1] = x[0] + (b1 - a1)/10 vals = [f(i) for i in x] if vals[1] < vals[0]: a1 = x[0] else: b1 = x[1] steps += 1 eps0[3].append(b1-a1) res.append(writer(a1, b1, steps-1)) lbls = ['Алгоритм равномерного поиска', 'Метод дихтомии', 'Метод золотого сечения', 'Метод Фибоначчи'] [print(lbls[i],'\n',res[i]) for i in range(len(res))] plt.plot(range(res[0]['steps']),eps0[0], label = lbls[0]) plt.plot(range(res[1]['steps']),eps0[1], label = lbls[1]) plt.plot(range(res[2]['steps']),eps0[2], label = lbls[2]) plt.plot(range(res[3]['steps']),eps0[3], label = lbls[3]) plt.legend() plt.show()

Результат выполнения кода представлен на рисунке 1.

Рисунок 1 – Результат выполнения кода

Код также строит графики зависимости числа итераций от погрешности для всех представленных методов в одних координатных осях и выводит результаты для каждого из методов.

Построение графиков зависимости числа итераций от погрешности для всех представленных методов в одних координатных осях;

Рисунок 2 – График зависимости числа итераций от погрешности для всех методов

Выводы об эффективности и трудоемкости представленных методов.

В ходе выполнения данной работы я произвел исследование заданной функции f(x)=(x^2)-9x+8 на экстремум на указанном интервале [4.2; 5.3] с помощью алгоритма равномерного поиска, метода дихотомии, метода золотого сечения и метода Фибоначчи.

На основе полученных результатов можно сделать следующие выводы об эффективности и трудоемкости представленных методов:

1. Алгоритм равномерного поиска имеет наименьшую трудоемкость среди всех представленных методов, но его точность зависит от выбора значения n для количества точек разбиения интервала.

2. Метод дихотомии имеет среднюю трудоемкость и обеспечивает хорошую точность результата.

3. Метод золотого сечения и метод Фибоначчи имеют наибольшую трудоемкость среди всех представленных методов, но обеспечивают высокую точность результата.

Таким образом, выбор метода для поиска экстремума функции зависит от требуемой точности результата и доступных вычислительных ресурсов. Если требуется высокая точность результата и доступны достаточные вычислительные ресурсы, то можно использовать метод золотого сечения или метод Фибоначчи. Если же требуется баланс между точностью результата и трудоемкостью алгоритма, то можно использовать метод дихотомии. Алгоритм равномерного поиска может быть использован в случаях, когда требуется быстрый поиск приблизительного решения.