Метод наименьших квадратов / Что говорить на слайдах

Слайд 1

Метод наименьших квадратов широко используется в регрессионном анализе. (набор статистических методов оценки отношений между переменными)

Слайд 2

На слайде изображена диаграмму рассеяния, где по горизонтали у меня отложен фактор икс, а по вертикали результативный показатель игрек. Точки на диаграмме показывают совокупность наблюдений. Здесь с ростом 1 показателя у нас растет и второй, что имеет выраженный линейный характер. На графике она в виде оранжевой прямой, имеющую вид (тык) . Прямая расположена так, чтобы она проходила максимально близко ко всем точкам.

А теперь зададимся вопросом, насколько хорошо построенная прямая описывает исходное наблюдение. Все отклонения исходных данных от точек на прямой изображено пунктирными линиями (тык). Чем они меньше, тем лучше.

Как эти отклонения измерить? Если я буду находить их сумму, как записано в 1 случае(тык) , то отрицательные отклонения в сумме с положительными будут гасить друг друга и мы не сможем узнать, насколько большими они были. Поэтому нужно рассчитывать (тык) сумму их квадратов и при суммировании они уже не будут гасить друг друга. Просчитав сумму квадратов отклонений мы узнаем, насколько близко или далеко расположена наша прямая от исходных точек на диаграмме. По сути это выражение это и есть метод наименьших квадратов. То есть Нам нужно найти такое значение неизвестных параметров, а 0 и а 1, чтобы полученная сумма квадратов отклонений была минимальной - отсюда и название метода. Ну, а теперь, прежде чем я расскажу, как находить а0 и а1, я покажу, какое влияние они оказывают на конечный результат.

Переход в эксель

На диаграмме всё те же наблюдения в виде точек их координаты x и y, приведенные в колонках «а» и «б». Также построен график прямой. Y расчетный. А 0 =19. А 1= -0.4. Такие параметры взяты специально, чтобы положение прямой не соответствовало общему характеру наблюдений. Координаты точек прямой рассчитываются в колонке С. Например, возьмем ячейку С5. К значению, а 0 прибавляем а1 и умножаем его на икс. В колонке Е измеряю квадраты отклонений между каждой точкой исходных данных Y и каждой точкой прямой - Y расчетным.

Внизу в ячейки Е17 нахожу их сумму. Это и есть сумма квадратов отклонений, которую нам нужно минимизировать. Когда мы здесь получим наименьшее возможное значение это будет означать, что прямая наилучшим образом описывает исходное наблюдение. А теперь давайте посмотрим, что будет происходить с ячейкой Е17, если мы начнем постепенно изменять параметры А 0 и А1. Сейчас у нас сумма квадрата в отклонении = 651,9 . Увеличим а1 до 0.9. При этом меняется также и угол наклона прямой. При а1=0,1 значение ячейки Е17 уменьшилось до 380,1. Если мы и дальше продолжим увеличивать а1, то сумма квадратов отклонений будет расти. То есть прямая начинает все дальше отдаляться от наших точек. Давайте теперь опустим нашу прямую. Я уменьшаю значение а0 до 10 и прямая начинает все ближе подбираться к исходным точкам. И отклонения в ячейке Е17 меньше. При а0 =10 ячейка Е17 =104,4 Если мы и дальше продолжим уменьшать, а 0, то отклонения начинают расти.

Как эти значения а0 и а1 находятся с помощью формул?

Мы будем минимизировать выражение , где Y расчетный зависит от неизвестных параметров, а0 и а1.

Слайд 3

Первое, что мы сделаем это подставим Y расчетный в наше выражение. Обозначим его функцией S. В данном случае исходные точки икс-игрек нам известны, а неизвестными переменными выступают а0 и а1. Именно их мы должны подобрать таким образом, чтобы минимизировать квадраты отклонений. Функция S будет принимать наименьшее значение, когда частная производная по обеим неизвестным будут равны 0. Далее идут обычные алгебраические преобразования. В конечном итоге получаем систему уравнений внизу.

Слайд 4

Из данной системы находим а0 и а1. И если поставить исходные данные, то получим, что а0=9.96, а1=0.94. То есть методом наименьших квадратов мы нашли такие а 0 и а1, которые наилучшим образом описывают исходное наблюдение.

Слайд 5

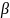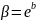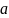Таким образом, эта задача свелась к предыдущей. Решая ее, находим значения коэффициентов a и b . Учитывая, что b=ln , находим . Подставим найденные значения и в уравнение (8) и получим искомую степенную функцию

Слайд 6

Слайд 7