контрольная работа № 3

где q(t) – амплитуда затухающих колебаний в момент времени t; ω –

циклическая частота затухающих колебаний:

Волны в упругой среде

Уравнение плоской бегущей волны

ξ ( l, t ) = A ∙ cos ω (t – l/ ) ,

где ξ (l, t) – смещение точек среды с координатой l в момент времени t; ω –

циклическая частота; – скорость распространения волны.

Длина волны λ связана с периодом T колебаний и циклической частотой

Волновая оптика. Интерференция света

Оптическая разность хода ∆ двух световых волн

∆ = L2 – L1 ,

где L – оптическая длина пути световой волны; L = nl. Здесь l – геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода ∆ световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки, находящейся в воздухе:

12

∆ = 2 d n2 sin 2 + 2 ,

где d – толщина пластинки; α – угол падения лучей. Слагаемое λ/2

обусловлено изменением фазы световой волны при отражении волны от среды с бóльшим показателем преломления (оптически более плотной среды). В

проходящем свете отражение световой волны происходит от оптически менее плотной среды и дополнительной разности фаз не возникает, поэтому для проходящих лучей слагаемое λ/2 в выражении для ∆ будет отсутствовать.

Условие максимумов интенсивности света при интерференции

∆ = m ,

где m = 1,2,3, . . .

Условие минимумов интенсивности света при интерференции

rm = mR .

Дифракция света

Положение минимумов освещенности при дифракции от щели, на которую нормально падает пучок параллельных лучей, определяется условием

a · sin φ = k λ ,

где а – ширина щели; φ – угол дифракции; λ – длина волны падающего света.

Условие главных максимумов интенсивности при дифракции света на дифракционной решетке (свет падает на решетку нормально)

13

d · sin φ = mλ ,

где d – период решетки (постоянная решетка); φ – угол дифракции (угол между направлением падающих на решетку лучей и дифрагированных лучей); m –

номер максимума.

Радиус зоны Френеля с номером m (для плоского фронта волны) rm = bm ,

где b – расстояние от фронта волны до точки наблюдения; m – номер зоны.

Поляризация света

Закон Брюстера

tg iБ = n21 ,

где iБ – угол Брюстера, т.е. угол падения, при котором отраженная от диэлектрика световая волна является полностью плоскополяризованной; n21 –

относительный показатель преломления. Относительный показатель преломления n21 равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:

n2 . n1

Скорость света в среде

nс ,

где с – скорость света в вакууме; n – абсолютный показатель преломления среды.

Закон Малюса

I = I0 cos2φ ,

где I0 – интенсивность плоскополяризованного света, падающего на анализатор,

I – интенсивность плоскополяризованного света, прошедшего через анализатор, φ – угол между направлением колебания светового вектора волны,

падающей на анализатор, и плоскостью пропускания анализатора.

14

Если неполяризованный свет интенсивностью I0 проходит через поляризатор, то прошедший свет становится плоскополяризованным,

интенсивность которого I связана с I0 следующим соотношением:

I = 12 I0 .

Примеры решения задач

П р и м е р 3.1

Материальная точка массой m = 10 г совершает гармонические колебания по закону синуса с периодом Т = 2 с и начальной фазой, равной нулю. Полная энергия колеблющейся точки W = 0,1 МДж. Найти: 1) амплитуду колебаний;

2) уравнение данных колебаний; 3) наибольшее значение силы Fmax,

действующей на точку.

Дано: m = 10 г = 0,01 кг, Т = 2 с, W = 0,1 МДж = 0,1 ∙106 Дж.

Найти: А =? Fmax = ? Уравнение – ?

Решение:

1. Уравнение гармонических колебаний имеет вид

х = А sin (ω0 t + φ0).

По условию задачи начальная фаза равна нулю, следовательно, уравнение гармонических колебаний принимает вид

х = А sin ω0 t.

Взяв первую производную смещения по времени, найдем скорость колеблющейся точки

dx

V = х′ = dt = A ω ∙ cos ω0 t.

Кинетическая энергия колеблющейся точки

15

Полная энергия колеблющейся точки равна максимальному значению ее кинетической энергии:

Отсюда находим следующее выражение для амплитуды колебаний:

Циклическая частота связана с периодом колебаний соотношением

ω0 = 2 .

Т

Подставляя его в выражение для амплитуды, получаем

Вычислим величину амплитуды:

Найдем численное значение циклической частоты:

2.Зная амплитуду колебаний и значение циклической частоты, можно записать уравнение гармонических колебаний для данной точки, м:

х= 0,045 ∙ sin πt .

3.Согласно второму закону Ньютона

смещения по времени (или, что то же самое, первую производную от скорости по времени):

Отсюда максимальное ускорение

16

amax A 02 .

Подставив это выражение максимального ускорения в соотношение (1),

найдем максимальную силу, действующую на точку:

Fmax = maω02.

Произведем вычисления:

Fmax = 0,01 ∙ 0,045 ∙ 3,142 = 4,44 ∙ 10-3 Н. Ответ: А= 0,045 м, Fmax = 4,44 ∙ 10-3 Н.

П р и м е р 3.2

Складываются два колебания одинакового направления, выраженные

φ2 составляющих колебаний; 2) амплитуду А и начальную фазу φ0

результирующего колебания. Написать уравнение результирующего колебания.

Дано: х1 = А1 ∙ cos ω(t + τ1) , x2 = A2 ∙cos ω(t + τ2), А1 = 1 см , А2 = 2 см ,

Для определения амплитуды А результирующего колебания удобно

воспользоваться методом векторных диаграмм. Суть его в том, что амплитуду А

17

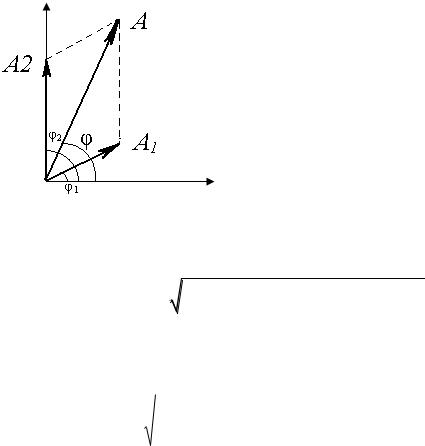
и начальную фазу φ0 результирующего колебания находят путем сложения векторов. Длина каждого вектора берется равной амплитуде соответствующего колебания, а угол, образованный вектором с осью ОХ, – начальной фазе.

Величины А и φ0 определяются длиной результирующего вектора и углом его наклона к оси ОХ.

На рисунке построена векторная диаграмма по условию данной задачи:

Согласно теореме косинусов амплитуда результирующего колебания определяется соотношением

Подставляя значения А1, А2 и (φ2 – φ1) в соотношение (3), произведем вычисления

Тангенс начальной фазы φ0 результирующего колебания определим по соотношению

Подставим значения А1, А2, φ1, φ2 и произведем вычисления:

18

Так как циклические частоты складываемых колебаний одинаковы, то

результирующее колебание будет иметь ту же частоту ω. Это позволяет написать уравнение результирующего колебания в виде

П р и м е р 3. 3

Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями х = А1 · cos t и y = А2 ∙cos t , где А1 = 1 см; А2 = 2 см; = π с-1. Найти уравнение траектории точки и построить траекторию с соблюдением масштаба, указать направление движения точки.

Дано: А1 = 1 см, А2 = 2 см. Определить: уравнение движения – ?

Решение:

Уравнение траектории точки, участвующей в двух взаимно

перпендикулярных колебаниях с амплитудами А1 и А2 и начальными фазами φ1

и φ2, имеет вид

Из условия задачи следует, что начальные фазы колебаний равны нулю,

следовательно, разность начальных фаз ( 2 1 ) также равна нулю, т.е.

2 1 = 0.

Сучетом этого уравнение траектории точки приобретает вид

Это уравнение можно записать следующим образом:

20