
03. Размещения, перестановки, сочетания
.pdf











 Свойства
Свойства





 биномиальных
биномиальных





 коэффициентов
коэффициентов





 (2)
(2)




































































































































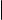






Докажем равенство 2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Cnk−1 + Cnk = |
|
n! |
|
|
|
+ |
|
n! |
|
= |
|
|
|
||||
(k − |
1)!(n − k + 1)! |
|
|
|
|
|
|
|
|
||||||||
|
|
k!(n − k)! |
|
|
|||||||||||||
= |
|
n! |
|
|
|
|
1 |
|
+ |
1 |
= |
|
|
||||
(k − |
1)!(n − k)! |
n − k + 1 |
k |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
n! |
|
· |
k + n − k + 1 |
|
= |
|
|
|
|||||||
(k − |
1)!(n − k)! |
k(n − k + 1) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
n!(n + 1) |
|
|
|
|
|
|
|
(n + 1)! |
k |
|
|||||
= |
|
|
= |
|
|
= Cn+1 |
, |
||||||||||
(k − |
1)!k(n − k)!(n − k + 1) |
k!(n + 1 − k)! |
|||||||||||||||
что и требовалось доказать.
§ 3. Размещения, перестановки, сочетания












 Биномиальная
Биномиальная





 формула
формула





 Ньютона
Ньютона





 (1)
(1)






































































































































































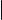








Пусть n произвольное натуральное число. Следующая формула называется биномиальной формулой Ньютона или просто биномом Ньютона:
n |
|
(x + y)n = X Cnk xn−k yk . |
(1) |
k=0
Эта формула и объясняет термин ¾биномиальные коэфиициенты¿: числа вида Cnk суть коэффициенты при одночленах в биноме Ньютона.
Доказательство биномиальной фомулы Ньютона проведем индукцией по n.
База индукции очевидна, так как (x + y)1 = x + y = C10x1−0 y0 + C11x1−1 y1 .
§ 3. Размещения, перестановки, сочетания












 Биномиальная
Биномиальная





 формула
формула





 Ньютона
Ньютона





 (2)
(2)















































































































































































Шаг индукции. Вычислим (x + y)n+1 , используя предположение индукции и свойства 1) и 2) биномиальных коэффициентов:
(x + y)n+1 = (x + y)n (x + y) =
=(xn + Cn1xn−1 y + · · · + Cnk xn−k yk + · · · + Cnn−1xyn−1 + yn )·
·(x + y) =
=xn+1 + Cn1 xn y + · · · + Cnk xn−k+1 yk + · · · + Cnn−1 x2yn−1 + xyn +
+xn y + Cn1xn−1 y2 + · · · + Cnk xn−k yk+1 + · · · + Cnn−1 xyn + yn+1 =
=xn+1 + (Cn1 + 1)xn y + · · · + (Cnk + Cnk−1 )xn−k+1 yk + · · · +
+(1 + Cnn−1)xyn + yn+1 =
=xn+1 + (Cn1 + Cn0 )xn y + · · · + (Cnk + Cnk−1 )xn−k+1 yk + · · · +
+(Cnn + Cnn−1 )xyn + yn+1 =
= xn+1 + C 1+ xn y + · · · + C k+ xn+1−k yk + · · · + C n+ xyn + yn+1 ,
n 1 n 1 n 1
что и требовалось доказать.
§ 3. Размещения, перестановки, сочетания












 Треугольник
Треугольник





 Паскаля
Паскаля


























































































































































































































































Удобным способом для того, чтобы быстро вычислить коэффициенты при одночленах в биноме Ньютона для небольших n служит так называемый треугольник Паскаля. Первые несколько его строчек выглядят так:
|
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
|
1 |
2 |
1 |
|
|
1 |
3 |
3 |
1 |
|
|
1 |
4 |
6 |
4 |
1 |
1 |
5 |
10 |
10 |
5 |
1 |
.. . . . . . . . . . . . . . . . . . . . . . . . . . .
Впервой строке треугольника Паскаля в центре записывается 1. В каждой следующей строке слева и справа от крайних элементов предыдущей строки пишутся 1, а посередине между каждыми двумя элементами предыдущей строки их сумма. Из свойства 2) биномиальных коэффициентов вытекает, что в n-й строке (если начинать нумерацию
строк не с единицы, а с нуля) слева направо будут записаны
биномиальные коэффициенты вида Cnk для k = 0, 1, . . . , n: нулевая строка соответствует равенству (x + y)0 = 1, первая равенству (x + y)1 = x + y, вторая равенству (x + y)2 = x2 + 2xy + y2 и т. д. В частности, согласно последней из выписанных нами выше строк треугольника Паскаля,
(x + y)5 = x5 + 5x4 y + 10x3 y2 + 10x2 y3 + 5xy4 + y5 .
5xy4 + y5 .
§ 3. Размещения, перестановки, сочетания
