Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kuznecov_reshebnik

.pdf

Скачиваний:

1095

Добавлен:

15.02.2015

Размер:

4.95 Mб

Скачать

☆

<<< < Предыдущая 12 / 322 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Уравнения первого порядка

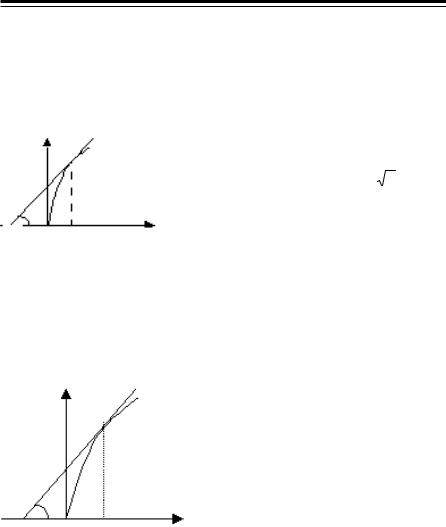
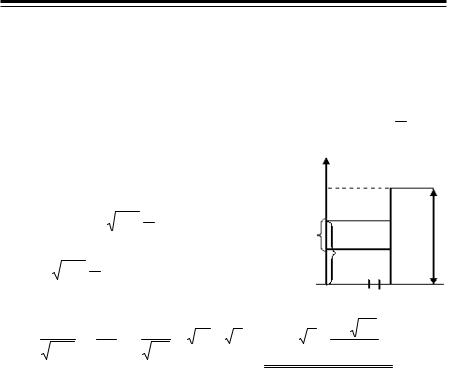
18 (3918). Найти линию, проходящую через точку (2; 0) и обладающую тем свойством, что отрезок касательной между точкой касания и осью ординатимеетпостоянную длину, равнуюдвум.

Решение

По условию

= 2. Из ∆

ABD

В .

= x =

cos (π − α ) = −2cos α =

.A(х,у)

D .

= −

1 + y

′2

1 + tg

+ y′

4 − x2

x = 2sin t,

4соs2t

y′ =

;

∫

dy =

∫

;

у =

∫

dt =

2sin t

dx = 2cos t dt

arcsin

= 2

+ cos t

= 2 ln

+ cos arcsin

= 2 ln tg

arcsin x

2 +


	x	= 2 ln
cos arcsin
cos arcsin	2
	2

		x
1 − cos arcsin					x2
1 − cos arcsin		2
		2	+ 2	1 −		=
	x		+ 2	1 −	4	=
	x				4
sin arcsin
sin arcsin	2
	2

1 −

+ 2 1 − x2

2 − 4 − x2

= 2 ln

+ 4 − x2

;

y = 2 ln 2 − 4 − x 2

4 − x 2

– уравнение трактрисы.

Примечание. Трактриса– плоскаякривая, обладающаятемсвойством, что длинаотрезкаеекасательноймеждуточкойкасанияинекоторойпрямой(базой трактрисы) естьвеличинапостоянная. ВнашемслучаебазойявляетсяосьОy.

Решебник задач по теме "Дифференциальные уравнения"

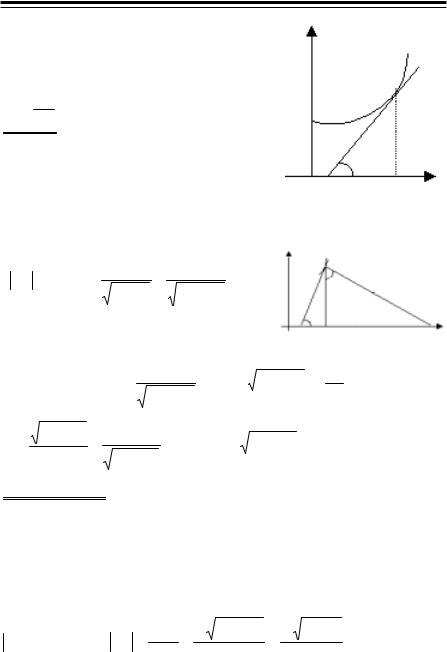
19 (3919). Найти все линии, у которых отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.

Решение

По условию

;

= x ;

= 2x.

.M(x,y)

Из ∆ АМK tg α =

y′ =

;

В .

+ ln c1; y = x c1

α .

y2 = cx

(c = c12 ) – параболы.

Дифференциальное уравнение можно

было составить, применив уравнение каса-

тельной АМ: Y − y = y′(X − x); X A = −x ; YA = 0

− y = y′(− 2x)

y = 2xy′.

20 (3920). Найтивселинии, укоторыхподкасательнаяпропорциональна абсциссе точки касания (коэффициент пропорциональности равен k).

Решение

По условию

= kx. Из ∆

АМВ

М(х,у)

имеем

. Значит,

= kx ,

tgα

y′

y dx

= kx ;

= ln

+ ln

; x1/ k

= c1 y

yk = cx , гдеc = c1−k.

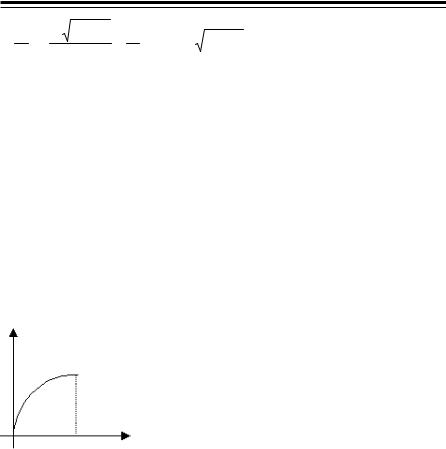
21 (3921). Найти линию, проходящую через точку (a; 1) и имеющую подкасательнуюпостояннойдлиныa.

Решение

По условию

= a . Из ∆ АМВ

tg α =

Уравнения первого порядка

+ ln c; ln

= ln eх/ а +

+ ln c

y = ceх/ а.

При х = а у = 1

1 = се с = е–1;

x − a

y = e a .

22 (3922). Найти линию, у которой длина нормали (отрезок ее от точки линии до оси абсцисс) есть постоянная величина a.

Решение

По условию

= a. Тогда

BC = asin α

a tg α

ay′

; (1)

1+ y′2

1+ (y′)2

tg α =

= yy′ .

(2) O K

′

ay′

a = y 1 + (y

′ 2

Из (1) и (2)

1 + (y′)2

)

O А

a2 y2

М(х,у)

Вх

C х

= 1 + (y′)2

y′ =	a2 − y2	;	y dy = dx x = − a2 − y2 + c a2 − y2 = (x − c)2	;
	y		a2 − y2

a2 = y2 + (x − c)2.

23 (3923). Найти линию, у которой сумма длин касательной и подкасательнойвлюбойееточкепропорциональнапроизведениюкоординатточки касания(коэффициентпропорциональностиравенk) (см. рисуноккзада-

че 22 (3922)).

Решение

= kxy ; KA =

y 1+ tg2α

= y

1+ y′2

;

sin α

tg α

y′

tg α

Решебник задач по теме "Дифференциальные уравнения"

=	y		y 1 + y′2	+	y	= kxy	1 + y′2 +1 = ky′x 1 + y′2 = k 2 y′2 x2 −
	y′		y′		y′

− 2ky′x +1

(k 2 x2 −1)dy = 2kx dx dy =

2kx

dx;

k 2 x2 −1

y =

k 2 x2 −1

+ c ;

y =

c (k 2 x2 −1)

, где

с =

ln c.

24 (3924). Найти линию y = f (x) ( f (x) ≥ 0, f (0) = 0), ограничивающую криволинейнуютрапециюсоснованием[0, x], площадькоторойпропорциональна (n + 1)-й степени f (x). Известно, что f (1) = 1.

Решение

По условию∫x

f (x)dx = k [f (x)]n+1. Продифференцируем обе части

f (x)= y

равенства:

;

(x)= k(n + 1)[f (x)] f ′(x)

y = k (n +1) yn y′ 1 = k(n +1) yn−1 dy

dx =

= k (n +1) yn−1 dy ∫dx = k (n +1)∫ yn−1dy

x = k (n +1) n

Из

f (1)= 1

следует 1 = k(n +1)

k =

. Тогда x = yn .

n +1

25 (3925). Материальная точка массой в 1 г движется прямолинейно поддействиемсилы, прямопропорциональнойвремени, отсчитываемому от момента t = 0, и обратно пропорциональной скорости движения точки. В момент t = 10 с скорость равнялась 0,5 м/с, а сила – 4 10–5 Н. Какова будет скорость спустя минуту после начала движения?

Уравнения первого порядка

Решение
m = 1 г = 10–3 кг		F = k	t			dV	= k	t
	По условию			,	m dt				.
	По условию		V	,	m dt			V	.
t = 10 с	Найдем k : 4 10−5 = k					10	k = 2 10−6 . Тогда
t = 10 с	Найдем k : 4 10−5 = k				0,5		k = 2 10−6 . Тогда
					0,5

V = 0,5 м/с				m	dV	= 2 10−6	t	mV dV = 2 10−6	t dt V 2 =
V = 0,5 м/с				m	dt	= 2 10−6		mV dV = 2 10−6	t dt V 2 =
					dt	V
F = 4 10–5 Н				= 2 10−3 t2 + c.
t		= 60 с		Найдем c: 0,25 = 2 10–3 100 + c					c = 0,05.
1
				Итак, V 2 = 2 10–3 t 2 + 0,05, откуда
V	1		– ?	Итак, V 2 = 2 10–3 t 2 + 0,05, откуда
	1
				V =		2 10−3 3600 + 0,05 ≈ 2,7 м/с .
				1

26 (3926). Материальная точка движется прямолинейно, причем так, что ее кинетическая энергия в момент t прямо пропорциональна средней скорости движения в интервале времени от нуля доt. Известно, что при t = 0 путь S = 0. Показать, что движение равномерное.

Решение

По условию Wk = kVср,

t = 0 = 0.

mV 2

= kVср

2kS

;

= k

∫

S =

t .

Обозначив

= V , получим S = Vt , т. е. движение равномерное.

27 (3927). Моторная лодка движется в спокойной воде со скоростью V = 10 км/ч. На полном ходу ее мотор был выключен, и через t = 20 с скоростьлодкиуменьшиласьдоV1 = 6 км/ч. Считая, что силасопротивле-

Решебник задач по теме "Дифференциальные уравнения"

нияводыдвижениюлодкипропорциональнаеескорости, найтискорость лодки через 2 мин после остановки мотора; найти также расстояние, пройденное лодкой в течение одной минуты после остановки мотора.

Решение
V = 10 км/ч
V = 10 км/ч					V
t = 20 сек = 1/30 ч			M		V
		R
		R
V = 6 км/ч
V = 6 км/ч	О S
t = 2 мин = 1/30 ч
t = 2 мин = 1/30 ч				P
t = 1 мин = 1/60 ч
V2 – ? S3 – ?

По закону Ньютона

= P + R ; mWx = Px+ Rx; R = − kV ;

= − kV

= − kV ; P = 0; W

Итак,

= − kV

= −

t + c V =

=ec1 e− m t V = ce− m t (c = еc1 ).

=10

10 = ce0 → c =10

V =10e−

t; V

= 6 6 =

ИзV

t = 0

=1/180

180

−

1/180

−

180

10e

m =

= (0,6) .

Итак, V = 10 (0,6)180 t ;

V2 = 10 (0,6)180 1/ 30= 10 (0,6)6 ≈ 0,467 км/ч;

1/ 60

[(0,6)3 −1]=

S3 = 10

∫

(0,6)180 t dt =

(0,6)180 t

1/ 60 =

180 ln 0,6

0,772

≈

0,085 км = 85 м .

9,194

28 (3928). В дне цилиндрического сосуда с поперечным сечением S и вертикальной осью имеется малое круглое отверстие площадью q, закрытое диафрагмой (как у объектива фотоаппарата). В сосуд налита

Уравнения первого порядка

жидкость высоты h. В момент t = 0 диафрагма начинает открываться, причем площадь отверстия пропорциональна времени и полностью отверстие открывается за Т секунд. Какова будет высота Н жидкости в сосуде через Т секунд после начала опыта?

Решение

Площадь отверстия δ = kt. При t = T

= q q = kT; k

Таким образом, δ

За время dt объем изменяется на вели-

чину S dx, за

то же время из отверстия вы-

течет жидкости

2gx

q t dt (ед. объема):

S dx = − 2gx

t dt;

∫t dt =

2 ( H − h )

= −S ∫

= −

h −

2gx

= Tq .

29 (3929). Скоростьохлаждениятелапропорциональнаразностимежду температурами тела и среды. В задачах (2710)–(2711) из [1] считаем коэффициентпропорциональностипостоянным. Принекоторыхрасчетах

считают, что он линейно зависит от времени: k = k0 (1 + α t ). Найти при этом предположении зависимость между температурой тела θ и временем t, полагая, что θ = θ 0 при t = 0, а температура окружающей среды θ 1.

Решение

dθ

= k0

+ α t)(θ − θ 1 );

= k0 (1 + α

t)dt

∫

= k0 ∫ (1 + α t)dt ;

θ − θ 1

θ −θ 1

θ 0

− θ

(2t + α t2 )

θ − θ

= k

t +

θ 0 − θ 1

Решебник задач по теме "Дифференциальные уравнения"

30 (3930). Скоростьростаплощадимолодоголиставиктории-регии, имеющего, какизвестно, формукруга, пропорциональнаокружностилиста и количеству солнечного света, падающего на лист. Последнее в свою очередьпропорциональноплощадилистаикосинусуугламеждунаправлением лучей и вертикалью. Найти зависимость между площадью S листа и временем t, если известно, что в 6 часов утра эта площадь равнялась 1600 см2, а в 6 часов вечера того же дня 2500 см2. (Полагать, что наблюдениепроизводилосьнаэкваторевденьравноденствия, когдаугол между направлением лучей солнца и вертикалью можно считать равным 90° в 6 часов утра и в 6 часов вечера и 0° в полдень.)

Решение

По условию S – площадь молодого листа виктории-регии;

= k

2π rk

S cosϕ . Но

S = π r2

π (t −12)

Изпропорции

: 6 = ϕ

− t :12

Таким образом,

dS =

2k k

S S cos

π (t −12)

Обозначив 2k1k2

π = k , получим

(t −

12)

(t −12)

= k cos

∫

= k ∫cos

dt;

S S

3 / 2

1600 S

12k

π (t −

12)

− 2

−

sin

+ 1 .

(*)

S(18)= 2500

12k

2 k =

Определим k:

−2

−

2400

Подставим

в (*):

−

= −

π (t − 12)

sin

+ 1

400

Уравнения первого порядка

	1		1			π	(t −12)			400			π	(t −12)
=		−			sin				+1		=10	− sin			−1
=	40	−	400		sin		12		+1	S	=10	− sin		12	−1
	40		400				12			S				12
S =			1600					.
S =					(t −			.
		9	− sin	π	(t −		12) 2

					12
					12

В задачах 31 (3931)–33 (3933) при помощи замены искомой функции привести данные уравнения к уравнениям с разделяющимися переменными и решить их.

31 (3931). y' = cos (x − y).

Решение

Положим u = x − y

y = x − u,

y' = 1 − u' ;

1 − u' = cos u

1 −

= cos u

= dx; ∫

+ c = ∫ dx

x + ctg

−ctg

+ c = x;

1− cos u

2sin

2 u

x − y

= c

x + ctg

= c .

32 (3932). y' = 3x − 2 y + 5.

Решение

Положим3x − 2 y + 5 = u

3 − 2 y' = u', y' =

−

u'. Тогда

−

u' = u;

−

= u

− u

dx =

dx + ln c1

∫ 3 − 2u

∫

−

3 − 2u

= x + ln c

3 − 2u

= ln e−2 x + ln c , где ln c =

– 2 ln c

;

3 − 2u = ce−2x

4 y − 6x − 7 = ce−2 x .

Решебник задач по теме "Дифференциальные уравнения"

33 (3933). y' 1 + x + y = x + y −1 .

Решение

Положим

1+ x + y = u

x + y = u2 −1, u' =

1 + y'

, y' = 2u' ×

1 + x + y

× 1

+ x + y −1 = 2uu' −1; (2uu' − 1)u = u 2 −1 − 1 2u 2u' = u 2 + u − 2 ;

u2du

2u2

= (u −1)(u + 2) 2∫

= ∫ dx + c ;

= 2 +

(u −1)(u + 2)

− 2u + 4

;

A =

; B = −

;

(u −1)(u + 2)

u −1

u + 2

2u +

u −1

−

u + 2

= x + c ,

где u =

1 + x + y .

Однородные уравнения

Взадачах 34 (3934)–44 (3944) найти общие решения уравнений.

34 (3934). y′

−

Решение

Обозначим

= u

y = xu ,

y′ = u + xu′; u + xu′ = u2 −

2; u + x

= u2 − 2

;

+ ln c

u2 − u − 2

∫

3 2 ∫

u −

−

1 ln

2u −1 − 3

= ln c1x

; 1 ln 2u − 4

= ln c1x

3 u − 2

= c1x

u − 2

u +1

3 2u −1 + 3

3 2u + 2

u +1

= cx3 (c3 = c);

u − 2 = cx3 (u +1)

y − 2x = cx3 (y + x).

<<< < Предыдущая 12 / 322 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015249.86 Кб7Kursova_robota_pochti_gotovaya.doc
#
15.02.20151.24 Mб16Kursovoy_Sistemy.docx
#
09.12.2018274.43 Кб9kurs_9.doc
#
19.08.2019138.24 Кб1Kurs_lektsiy.doc
#
15.02.2015979.17 Кб19Kuznecov_Praktikum.pdf
#
15.02.20154.95 Mб1095Kuznecov_reshebnik.pdf
#
15.02.20158.28 Mб43Kvasnickij_Pajka_mat.pdf
#
14.02.2015755.2 Кб41Lab1_kl_metod.doc
#
14.02.20152.66 Mб34Lab2_KL_metod.doc
#
14.02.2015547.06 Кб26Laba_1.docx
#
14.02.2015177.15 Кб7Laba_2.doc