
_books_met_files_fund_radio_el
.pdf
|
|
|
|
|
|
|
|
|
|
11 |
|
|
||
|
|
an |
|
2 |
|
TT2 U t cosn 1tdt; |
(2.14) |
|||||||
T |
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|||||
|
bn |
2 |
|
TT2 |
U t sinn 1tdt. |
|
||||||||
T |
|
|||||||||||||
|
|
|
|
|
2 |
|
||||||||
Из полученного выше выражения для ряда Фурье имеем |
|
|||||||||||||
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
||
|
|
U t |
|
|
an cosn 1t bn sinn 1t |
. |
(2.15) |
|||||||
|
||||||||||||||
Итак: |
|
|
|
|
|
2 |
|
n 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) В общем случае сложный периодический сигнал может иметь постоянную |
||||||||||||||
составляющую и бесконечный набор гармонических колебаний с частотами |
|
|||||||||||||
i = i 1. |
|
|
x |
|
|
|
|
|
|
|
||||
-T/2 |
|
0 |
|
|
|
|
|
T/2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.5
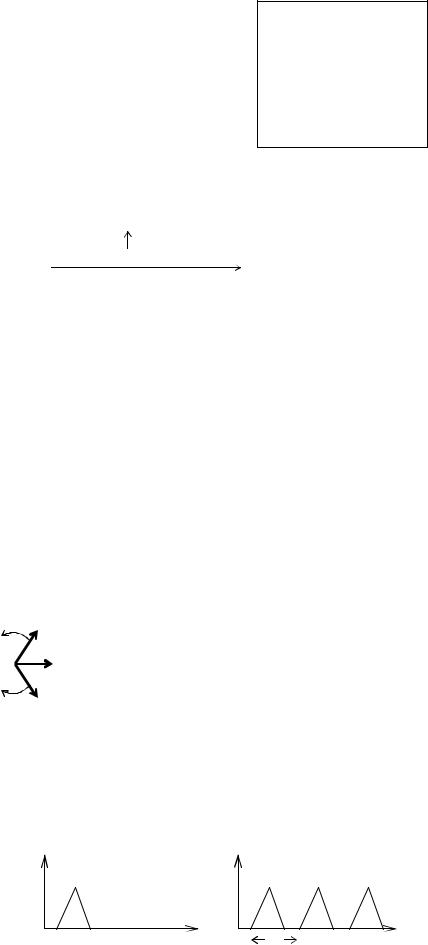
Отметим, чем больше составляющих i 1, тем ближе сумма составляющих к истинному сигналу (см. рис. 2.5).
2) Четный сигнал имеет только косинусоидальные слагаемые (т.к. bn обращаются в ноль), нечетный — только синусоидальные (т.к. an обращаются в ноль).
Каждую гармоническую составляющую можно описать ее амплитудой An и начальной фазой n, т.е. спектр периодического сигнала линейчатый (см. рис. 2.6).
an An |
cos n, |
bn An sin n, |
|
|||||
где An |
|
|
, n arctg |
bn |
. |
|
||
|
an2 bn2 |
|
||||||
|
|
|
||||||
Тогда |
|
|
|
|
an |
|
||
|
|
|
a0 |
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
U t |
An cos n 1t n . |
(2.16) |
|||
|
|
|
|
|||||
|
|
|
2 |
|
n 1 |
|
||
Амплитудный спектр |
|
Фазовый спектр |
|
|||||
An |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
0 |
|
1 |
|
3 |
|
4 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
0 1 2 3 4 |
|
2 |
|
||||||||||
Рис. 2.6

12
2.3.2. Комплексная форма ряда Фурье
Спектральное разложение периодического сигнала можно выполнить, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
|
|
|
|
|
l |
n |
exp |
jn |
1t , |
n 0, 1, 2,... |
|
(2.17) |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Действительно, функции этой системы периодичны с периодом T |
||||||||||||||||||||||||||
ортонормированны на отрезке времени T |
,T |
. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
||
Доказательство ортонормированности |
|
|
|
|
|
|||||||||||||||||||||
lm,ln TT2 lm t ln* t |
dt |
1 |
|
TT2 exp jm 1t exp jn 1t dt |
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
1 |
|
2 |
|
|
T |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
TT2 exp j m n 1t dt; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сделаем замену переменных: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
t x, t |
|
x |
, так как |
|
2 |
, то t xT , dt |
T |
|
dx |
|
||||||||||||||||
|
|
|
|
T |
2 |
|
||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
при t T |
1 |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
, x , при t |
|
, |
|
x , получим |
|
|
||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 при m n |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
lm,ln |
|
|
|
|
ej m n xdx |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 при m n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ряд Фурье (2.11) произвольного периодического сигнала в данном случае принимает вид:
U t Cnln t , или с учетом (2.17)
n |
1 |
|
|
|
U t |
|
|||
|
Cnejn 1t . |
|||
|
|
|
||
|
|
|||
|
|
T n |
||
Найдем коэффициенты разложения Cn. Для этого левую и правую часть
домножим на |
e jk 1t |
и возьмем интеграл TT2 |
. Получим |
||||||||
|
|
T |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
1 |
2 |
|
t e jn 1tdt. |
|||
|
|
|
|
Cn |
|
TU |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
T |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обычно используют несколько иную запись:
13
|
|
|
|
|
|
U t Cnejn 1t |
|
||||
|
n |
|
|
||
|
|
T |
. |
(2.18) |
|
|
1 |
2 |
|||
|
t e jn 1tdt |
|
|||
Cn |
TU |
|
|||
T |
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
Выражения (2.18) представляют ряд Фурье в комплексной форме. Спектр сигнала в соответствии с этими выражениями содержит компоненты на положительной и отрицательной полуоси, причем
|
|
|
|
|
|
|
|
Сn |
|
|
|
|
|
C n |
Cn*. |
|
|
|
|
(2.19) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
-2 |
-1 |
0 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
При переходе к тригонометрической форме записи получим |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t C0 |
|
|
|
cos n 1t n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Cn |
|
(2.20) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Из сравнения (2.16) и (2.20) видно, что |
n 1 |
|
T |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
An 2 |
|
Cn |
|
, |
an 2Cnc |
2 |
TU t cosn 1tdt, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
bn |
|
2Cns |
2 |
TU t sinn 1tdt. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После |
перехода к тригонометрической форме понятие “отрицательная” |
|||||||||||||||||||||||||
|
|
Im |
|
|
частота |
теряет |
смысл, |
т.к. это |
|
понятие не |
физическое, а |
|||||||||||||||||
+ |
|
|
|
математическое, |
вытекающее |
|
из |
способа |
представления |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Re |
комплексных |
|
чисел. Положительной |
частоте |
соответствует |
|||||||||||||||||||||
0 |
|
|
вектор, |
вращающийся против часовой стрелки, а отрицательной |
||||||||||||||||||||||||
- |
|
|
|
|
|
|
частоте — вектор, вращающийся по часовой стрелке. |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
2.4. Спектральное представление непериодических сигналов
Пусть U(t) одиночный импульс конечной длительности. Создадим периодическую последовательность с периодом T и представим ее комплексным рядом Фурье (см.2.18).
U |
|
Uпер |
|||
t |
|
|
|
|
t |
0 |
0 |
|
T |
|
|
|
|
||||
Рис. 2.7 |
|
|
|
|
|
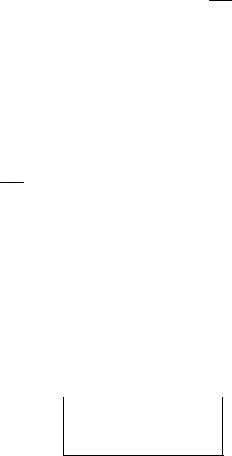
14
Uпер t |
|
|
|
||
Cnejn 1t , |
(2.21) |
||||
где |
|
n |
|
||
T |
|
||||
|
|
|
|||
|
1 |
2 |
|
||
Cn |
TU t e jn 1tdt. |
(2.22) |
|||
T |
|||||
|
|
|
2 |
|
|
|
|
|
|
||
Для того, чтобы перейти к спектральному представлению единичного импульса, устремим T .
Из (2.22) видно, что при T получаем:
-бесконечно-малые амплитудные коэффициенты Cn (из-за наличия T в знаменателе);
-частоты соседних гармоник n 1 и (n+1) 1 становятся сколь угодно
близкими (т.к. 1 2T );
- число гармоник, входящих в ряд Фурье, становится бесконечно большим, т.к. при T , основная частота 1 2T 0, т.е. спектр становится
сплошным.
Подставив (2.22) в (2.21), получим:
|
|
|
T |
|
|
|
|
|
|
2 |
|
1 |
|
||
U t |
|
U |
x e jn 1xdx ejn 1t |
, |
|||
2 |
|||||||
|
n |
T |
|
|
|||
|
|
|
2 |
|
|
|
|
т.к. T , то 1 2T 0, поэтому в этом выражении можно заменить
1 d ; n 1 ; . Таким образом, переходим к двойному интегралу Фурье:
|
|
1 |
|
|
|
|
|
|
|
U t |
|
ej t |
U |
x e j xdx d . |
|||
|
2 |
|||||||
|
|
|
|
|
|
|
||
x e j xdx S |
|
|
|
|||||
Здесь обозначим U |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S U t e j tdt |
(2.23). |
||||
|
|
|
|
|
|
|
|
|
S - спектральная плотность сигнала U t или прямое преобразование
Фурье, или Фурье-образ сигнала. Отсюда:

15
|
1 |
|
|
|
U t |
S ej td . |
(2.24) |
||
2 |
||||
|
|
|
||
|
|
|
Это обратное преобразование Фурье.
Физический смысл S
Спектральная плотность – это отношение комплексной амплитуды малого интервала частот вблизи частоты, равной f0, к длине этого интервала. Причем вклад дают как положительные, так и отрицательные частоты, образующие окрестность f0.
Спектральная плотность — комплекснозначная функция частоты, одновременно несущая информацию об амплитуде и о фазе элементарных синусоид.
Таким образом, из (2.23) и (2.24) следует, что один и тот же сигнал допускает две совершенно равноправные математические модели — временную и частотную.
Условия существования S - это абсолютная интегрируемость сигнала, т.е.
|
t |
|
|
|
|
|
|
|
||
|
|
U |
|
dt . |
(2.25) |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
Можно записать S A jB |
|
S |
|
e j , где: |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A U |
t cos t dt; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B U |
t sin t dt. |
||||||
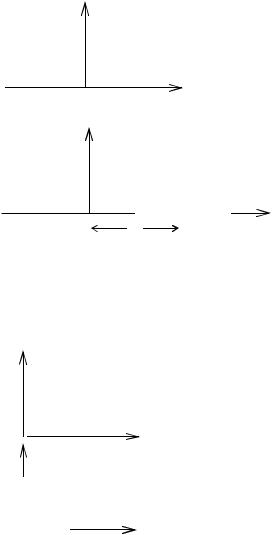
Тогда амплитудно-частотная характеристика (АЧХ) сигнала –
S 
 A2 B2 ;
A2 B2 ;
Фазо-частотная характеристика (ФЧХ) сигнала - arctg BA .
16
2.4.1. Основные свойства преобразований Фурье
Итак, между сигналом U t и его спектральной плотностью S существует
однозначное соответствие, устанавливаемое соотношениями (2.23) и (2.24). Для практических целей важна связь между различными преобразованиями сигнала и соответствующими изменениями спектра. Рассмотрим основные из этих преобразований.
1) Сложение сигналов. Если
U t U1 t U2 t ... Un t ,
то
S S1 S2 ... Sn ,
т.е. преобразование Фурье линейно. Пример: сигнал+помеха
2) Сдвиг сигналов во времени (теорема запаздывания).
|
U1 |
|
|
|
|
U2 t U1 t t0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
U1 t t0 e j t |
|
|
|
|
|
|
||
|
|
|
|
|
t |
|
|
|
|
|
|
|
обозначим t t0, dt |
||
|
|
|
|
|
|
||
0 |
|
|
|
|
|||
|
|
|
|
|
e j t0 d e |
||
|
|
|
|
|
|
||
|
U2 |
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
S2 e j t0 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
0 |
|
t0 |
|
|
|
|
|
|
|
|
|
||||
(2.26)
dt
d
j t0 S1 ;
S1 (2.27)
Рис.2.8
Отсюда видно, что АЧХ сигнала остается постоянной, но меняется его фазовая характеристика.
Пример: фильтрация РЛС сигналов.
|
U1 |
|
|
|
|
3) Изменение масштаба времени. |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
U2 t U1 nt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
n>1 – сжатие сигнала, |
|
|
|
|
|
|
|
|
t |
n<1 – расширение сигнала |
|
|
|
||
U2 |
|
|
и |
|
|
|
||||
|
|
|
|
|
|
u /n |
u /n |
|
|
|
|
|
|
|
|
|
S2 U2 |
t e j tdt U1 |
nt e j tdt. |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
t |
После замены переменных nt , |
dt d n |
отсюда имеем |
||
|
и/n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис.2.9

17
S |
|
|
1 |
u |
|
|
|
e |
j |
|
d |
1 |
S |
|
|
|
|
|
U |
|
|
n |
n |
|
|
||||||||
|
2 |
|
n 0 |
|
|
1 |
|
|
|
|
|
1 |
n |
|||
|
|
|
|
S |
|
|
1 |
S |
|
|
, |
|
|
(2.28) |
||
|
|
|
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
1 |
n |
|
|
|
|
||
т.е при сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр и уменьшается интенсивность спектральной плотности.
Из этого свойства и примеров по определению спектральных плотностей импульсов видно, что чем меньше длительность сигнала, тем шире его спектр.
Для установления количественных соотношений между указанными параметрами необходимо определиться с понятием длительности сигнала и ширины его спектра. В большинстве случаев выбор произвольный.
Например:
-для прямоугольного импульса ширина спектра принимается как
основание главного лепестка fв и 1;
-для колоколообразного импульса ширина берется на уровне 0,606 от максимального значения;
-можно также использовать энергетический критерий (например 90%
энергии и т.д.). В результате fв и constи зависит от формы импульса. Минимальная fв и 0,5у колоколообразного (гауссового) импульса. Пример: спектральный анализ с временной компрессией.
4) |
|
Произведение двух сигналов. |
||||
U t f t g t , |
||||||
где |
|
|
|
|
|
|
f t |
1 |
|
ej td , |
|||
|
F |
|||||
|
2 |
|||||
|
|
|
|
|||
g t |
1 |
|
|
ej td . |
||
|
G |
|||||
2 |
||||||
|
|
|
||||
Найдем прямое преобразование Фурье:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
S |
U t e j tdt f |
t |
g t e j tdt |
|
f t G |
x ejxtdx e |
||||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
G x f t e j x tdt dx |
G |
x F x dx, |
|
||||||||||||
2 |
2 |
|
||||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
S |
1 |
|
|
x F x dx |
|
|
|
|
|
|||
|
|
|
|
G |
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- свертка спектров сомножителей.
j t
dt
(2.29)

18
Примеры: преобразование частоты; исследование флуктуаций; получение спектра радиоимпульса как произведение синусоидального сигнала sin t на прямоугольный импульс.
5) Спектральная плотность производной сигнала и его интеграла. f t dUdt ,
|
dU e j tdt. |
|
|
|
|
F |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя по частям U Vdt UV UV dt, получим |
|||||
|
|
|
|
|
|
|
F U t e j t |
|
j U t e j tdt . |
||
|
|
||||
|
|
|
|
|
|
Если выполняется условие |
limU t 0, то |
||||
|
|
t |
|
||
|
|
|
|
|
|
|
|
|
|
|
F j S |
, |
|
где |
|
j e |
j |
|
(т.к. |
|
по |
формуле |
Эйлера |
||||
|
|
2 |
|
||||||||||
S |
|
S |
|
e j , |
|
S |
|
- амплитудный |
спектр и |
||||
|
|
|
|
||||||||||
исходного сигнала U(t), или |
|
|
|
||||||||||
(2.30) ej2 cos 2 jsin 2 j);
( ) – фазовый спектр
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
S |
e |
|
|
|
, |
|
(2.31) |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.е. изменится амплитудный спектр, а фазовый спектр меняется на |
на всех |
||||||||||||||||||||
частотах. |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
S |
|
, |
|
F |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
Если |
|
S |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0
Рис. 2.10
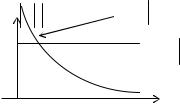
Причем дифференцирование поднимает верхние частоты и занижает низкие
частоты. |
|
|
|
|
|
|
|
|
|
|
|
Аналогично можно найти спектр интеграла g t U t dt. |
|
||||||||||
Представив U t dg , следовательно, |
S j G , отсюда |
|
|||||||||
|
dt |
|
|
|
|
S |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
G |
|
S |
|
|
j |
|
|
|||
|
|
|
|
|
e |
|
2 |
(2.32) |
|||
j |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
19
G, S
 G
G
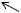
 S
S
0
Рис. 2.11
6) Теорема Парсеваля.
Известно, что энергия колебания на единичном сопротивлении E U2 t dt.
Найдем соотношение, позволяющее определить энергию колебания U(t) посредством использования его спектра. Для этого воспользуемся прямым преобразованием Фурье
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t |
|
|
S ej td . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Умножим обе части данного равенства на U(t) и проинтегрируем в |
||||||||||||||||||||||||||||||
бесконечных пределах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
U2 t dt |
|
|
S |
U |
t ej tdt d , |
|||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||
но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t ej tdt S* , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 d . |
||||||||
таким образом E |
|
|
S |
S* d |
|
S |
||||||||||||||||||||||||
2 |
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Т.к. квадрат модуля есть четная функция , то, удвоив значение интеграла, |
||||||||||||||||||||||||||||||
можно проводить интегрирование в пределах 0 — . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t dt 1 |
|
|
|
2 d |
|
|
|||||||||
|
|
|
|
|
|
|
E U2 |
|
|
S |
(2.33) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Из этого соотношения следует, что на бесконечно малый участок частот d |
||||||||||||||||||||||||||||||
приходится энергия E |
|
S |
|
2 |
d dE d , |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
S |
|
2 — энергетический спектр сигнала. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
Величина dE |
|
|
S |
|
2 |
|
|
— спектральная плотность энергии колебания U(t). |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Полная энергия сигнала равна сумме энергий всех его частотных составляющих.
Пример - спектральный анализатор.
20
7) Обобщенная формула Рэлея.
Пусть два сигнала U(t) и V(t) (в общем случае комплексные) определены своими обратными преобразованиями Фурье:
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
V t |
|
Sv ej td ; |
|
|
V* t |
|
|
|
Sv* e j td , |
|
|||||||||||||
2 |
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t |
|
Su ej td . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем скалярное произведение |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
U,V U |
t V* t dt |
1 |
|
|
|
U |
t Sv* e j td dt |
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Sv* U t e j tdt |
d |
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
U,V |
|
1 |
|
|
Sv* d |
1 |
SuSv |
|
|
|||||||||||
Отсюда |
|
|
|
Su |
|
|
|||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
,V |
|
1 |
SuSv |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
— Формула Рэлея |
(2.34) |
||||||||||||||||
|
|
|
2 |
||||||||||||||||||||
Скалярное произведение двух сигналов с точностью до коэффициента 21
равно скалярному произведению их спектральных плотностей.
Пример - ортогональность неперекрывающихся по спектру сигналов.
2.4.2 Спектральная плотность некоторых неинтегрируемых сигналов
Математические модели многих сигналов не удовлетворяют условию абсолютной интегрируемости (2.25) и поэтому метод преобразований Фурье в обычном виде к ним не применим. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что эти плотности описываются обобщенными функциями.
1) Спектральная плотность функции.
U U
|
|
|
|
U t t t0 |
, t t0 |
|
|
|
|
|
|
t t0 |
|
|
|
|
|
E=1/ u |
0, |
|
0 |
|
|
|
t |
|
|
t- u/2 t0 |
|
|
|
|||
t+ u/2 |
|
|
||||
Рис. 2.12
