
Теория вероятностей
.pdfТеорема 4. Если события |
и |
совместные, то |
|
Теоремы умножения(. |
+ |
) = ( ) + ( ) − ( ). |
(1.9) |
События и называются независимыми, если появление одного из них не
влияет на вероятность появления другого (в противном случае события зависимы).
События |
, , …., |
называются попарно независимыми (или независимыми в |
||||||||||||||||||||
совокупности), если каждые два из них независимы. |
|
|
|
|
|
|
|
|
||||||||||||||
Теорема 1. Если события |
и |
независимые, то |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Теорема 2. Если события |
, |
,(….,) = попарно( )∙ (независимы). |
, то |
|
|
|
(1.10) |
|||||||||||||||
|
|
|
|
|
|
n |
|
n |
|
|
i |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
(1.11) |
||||
|
|
|
|
|
P |
A |
|
|
P A |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 3. Если события |
и |
зависимые, то |
( ) ( ) |
|
|
|
|
|
|
|
||||||||||||
где |
|
- |
( |
) = |
( ) |
( |
) = |
|
|
|
|
|
|
|
|
(1.12) |
||||||
условии( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
и |
|
условные вероятности. |
- |
|
вероятность события |
при |
||||||||||||||||
,)что событие( ) |
уже произошло. Для условной( ) |
вероятности |
( |
) |
есть еще |
|||||||||||||||||
обозначение P(A/B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема 4. |
Вероятность) |
появления хотя бы одного из событий |
, |
|
, |
…., |
||||||||||||||||
независимых в совокупности, равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
P(A1 A2 |
... An ) 1 P( |
|
|
|
2 ) ... P |
|
n . |
|
|
|
(1.13) |
||||||||
|
|
|
A1) P( |
А |
A |
|
|
|
||||||||||||||
Пример 9. Вероятность попадания в мишень при каждом выстреле для первого стрелка равна 0,7, а для второго – 0,8. Оба они делают по одному выстрелу
по мишени. Найти вероятности событий: |
– |
в мишени две пробоины; |
– в |
|||||||||||||
мишени только одна пробоина; – в мишени хотя бы одна пробоина. |
|
|
|
|||||||||||||
Решение. Введем два события: |
={в мишень попал первый стрелок}, |
={в |
||||||||||||||
мишень попал второй стрелок}. Тогда |
|
|
, события |
и |
|
– независимые, |
||||||||||
применяя формулу (1.10), находим |
вероятность события |
|
|
|
|
|
|
|||||||||
|
|
|
= |
)∙ ( |
) = 0,7∙0,8 = 0,56 |
|
|
|
||||||||
Теперь найдем( ) = ( ∙ |
) = |
|
( |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вероятность события . В мишени одна пробоина означает, |
||||||||||||||||
что попал либо первый, либо второй, |
т.е. |
В А1 |
|
|
|
А2 . Выстрелы производятся |
||||||||||
А2 |
А1 |
|||||||||||||||
независимо, поэтому события |
и |
|
|
– независимые, события |
|
и |
– так же |
|||||||||
|
|
|||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|

независимые, |
а два события |
А1 А2 и |
А1 А2 |
- несовместные. Используя теоремы |
||||||||||
сложения и умножения, имеем |
|
|
|
|
|
|
|
|||||||
Р(В) Р(А1 |
|
|
|
А2 ) Р(А1 |
|
) Р( |
|
А2 ) 0,7 0,2 0,3 0,8 0,38. |
||||||
А2 |
А1 |
А2 |
А1 |
|||||||||||
Вероятность события С находим по формуле (1.13) |
||||||||||||||
|
|
Р(С) 1 Р( |
|
|
|
|
||||||||
|
|
А1)Р(А2 ) 1 0,3 0,2 0,94. |
||||||||||||
Пример |
1.10. Найти |
вероятность |
прохождения тока через цепь при |
|||||||||||
последовательном соединении, если вероятности исправной работы элементов равны и . Элементы работают независимо друг от друга.
 р1
р1  р2
р2
Решение. Введем два события: A1 {первый элемент работает}, A2 {второй элемент работает}. При последовательном соединении ток пройдет по цепи только тогда, когда оба элемента работают. Тогда событие C {ток идет по всей цепи}
можно записать в виде
C А1 А2 .
События A1 и A2 независимые, следовательно, по формуле (1.10) имеем
( ) = ∙
Пример 1.11. Найти вероятность прохождения тока через цепь при параллельном соединении, если вероятности исправной работы элементов равны
и. Элементы работают независимо друг от друга.
 р1
р1
 р2
р2
Решение. При параллельном соединении ток пройдет по цепи только тогда,
когда хотя бы один из двух элементов работает. Введем два события: A1 {первый элемент работает}, A2 {второй элемент работает}. Тогда событие C {ток идет по всей цепи} можно записать в виде
C А1 А2 А1 А2 А1 А2 .
11
Однако противоположное событие С можно представить в более компактном
виде
С А1 А2 .
События A 1 и A2 - независимые. Обозначим Р(А1) q1 Р(А2 ) q2 , тогда
Р(С) Р(А1 А2 ) Р(А1) Р(А2 ) q1 q2 .
По следствию теоремы сложения 3 имеем
Р(C) 1 Р(C) 1 q1 q2 1 1 p1 1 p2 .
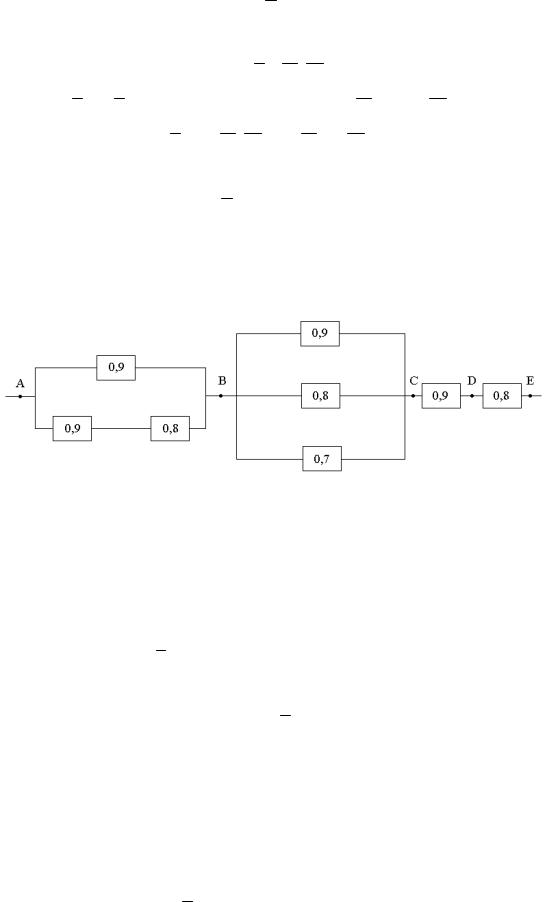
Пример 1.12. Найти вероятность прохождения тока через цепь, если вероятности исправной работы элементов указаны на схеме. Элементы работают независимо друг от друга.
Решение. Введем события: A1 - ток идет по участку АВ, A 2 - ток идет по участку ВС, A 3 - ток идет по участку СЕ. Согласно примеру 10, вероятность того,
что ток идет по участку СЕ равна
P(A3) 0,9 0,8 0,72.
Следуя примеру 11, вероятность того, что ток по участку ВС не идет равна
P(A2 ) 1 0,9 1 0,8 1 0,7 0,006.
Тогда вероятность того, что ток по участку ВС идет равна
P(A2 ) 1 P(A2 ) 0,994.
Участок АВ состоит из параллельного и последовательного соединения.
Вероятность того, что ток идет по нижнему участку АВ равна
P 0,9 0,8 0,72.
Тогда вероятность того, что по всему участку АВ ток не идет, вычисляем как для параллельного соединения (см. пример 11)
P(A1) 1 0,9 1 0,72 0,028.
А вероятность того, что по участку АВ ток идет равна
12
P(A1) 1 0,028 0,972.
Соединение АВ, ВС, СЕ – последовательное, поэтому вероятность того, что ток
идет по всему участку АЕ равна
PP A1 P A2 P A3 0,972 0,994 0,072 0,696.
1.5.Формула полной вероятности. Формула Байеса
Теорема. Если событие A может произойти только при условии появления одного из попарно несовместных событий (гипотез) В1,В2, ... Вn , образующих полную группу, то вероятность события A равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события A
n |
|
P(A) P(Bi )P(A/ Bi ) P(B1)P(A/ B1) P(B2 )P(A/ B2 ) ... |
P(Bn )P(A/ Bn ) (1.14) |
i 1 |
|
Из теоремы умножения (1.12) и формулы полной вероятности (1.14) легко получить формулу Байеса, которая позволяет «переставить причину и следствие»:
по известному факту события позволяет вычислить вероятность того, что оно было вызвано данной причиной.
Теорема. Условная вероятность гипотезы Bi , при условии того, что событие
A произошло, вычисляется по формуле Байеса
P(B / A) |
P(Bi ) P(A/ Bi ) |
, |
(1.15) |
|
n |
||||
i |
|
|
P(Bi ) P(A/ Bi )
i 1
где В1 , В2, ... ,Вn - попарно несовместные события, образующие полную группу.
Вероятности Р(Вi ) называют априорными вероятностями, т.е. вероятностями событий до выполнения опыта, а условные вероятности этих событий ( / )
апостериорными, т.е. уточненными в результате опыта, исходом которого послужило появление события А.
Пример 1.13. Имеются две партии однотипных изделий. Первая партия состоит из 60 изделий, среди которых 10 бракованных, вторая из 40 изделий, среди которых 5 бракованных. Из первой партии берется случайным образом 25 изделий,
а из второй – 15. Эти изделия смешиваются и образуется новая смешанная партия,
13

из которой берется наугад одно изделие. Найти вероятность того, что оно будет бракованным.
Решение. Введем события В1 ={извлеченное из смешанной партии изделие оказалось из первой партии}, В2 ={извлеченное из смешанной партии изделие оказалось из второй партии}, А={извлеченное из смешанной партии изделие бракованное}.
Тогда по формуле (1.4) имеем P B |
25 |
, |
P B |
|
|
15 |
. Вероятность выбрать |
1 |
40 |
|
|
2 |
40 |
|
|
дефектное изделие из смешанной партии, при условии что осуществилось событие
В1, |
равна ( |
/ ) = |
|
; а |
при условии |
что осуществилось событие В2, равна |
|||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
вероятности (1.14) получаем |
|||||||||||
( |
/ ) = . |
По формуле полной |
|||||||||||||||||
25 |
10 |
|
|
15 |
|
5 |
0,1042. |
||||||||||||
|
|
|
|
|
|
|
P(A) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
40 |
|
40 |
40 |
|||||||||
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|||||||
|
Пример |
1.14. Среди |
поступающих |
|
на |
сборку деталей с I станка 0,1% |
|||||||||||||
бракованных, со II-0,2%; с III- 0,25%, с IV – 0,5%. Производительности их относятся соответственно как 4:3:2:1. Взятая наудачу деталь оказалась стандартной. На каком станке вероятнее всего она изготовлена?
Решение. Введем события: А ={взятая деталь стандартная}, |
={взятая деталь |
|||||||||||||||||||||||||
изготовлена |
4на |
–ом4 |
станке}, |
|
3= 1,2,3,4. |
2 |
|
|
1 |
|
|
будут равны: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятности гипотез |
||||||||
Р(В1) |
|
|
|
|
|
|
|
, |
Р(В2 ) |
|
|
|
, Р(В3) |
|
|
|
, Р(В4 ) |
|
|
|
. Условные вероятности: |
|||||
4 3 2 1 |
10 |
10 |
|
10 |
|
10 |
||||||||||||||||||||
P(A/B ) 1 |
0,1 |
|
0,999, |
P(A/B |
2 |
) 0,998, |
|
P(A/ B ) 0,9975, P(A/ B ) 0,995. |
||||||||||||||||||
|
||||||||||||||||||||||||||
1 |
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда по формуле (1.14) найдем вероятность того, что наудачу взятая деталь |
||||||||||||||||||||||||||
оказалась стандартной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
P(A) |
4 |
0,999 |
|
3 |
0,998 |
|
2 |
0,9975 |
|
1 |
0,995 0,998. |
||||||||||
|
|
|
|
|
10 |
|
|
|
10 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
10 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|

Применим формулу Байеса (1.15), чтобы найти вероятность того, что извлеченная деталь, оказавшаяся стандартной, изготовлена на I станке.
|
P(B1) P(A/ В1) |
|
|
4 |
0,999 |
|||
|
|
|
|
|||||
P(B / А) |
|
10 |
|
0,4004. |
||||
|
|
|
||||||
1 |
|
P(A) |
0,998 |
|
||||
|
|
|
||||||
Аналогично, P(B2 / A) 0,3000, |
P(B3 / A) 0,1999, |
P(B4 / A) 0,0997. |
||||||
Таким образом, вероятнее всего, что деталь изготовлена на первом станке.
1.6.Повторение испытаний
Пусть |
проводится |
конечное |
число |
последовательных |
независимых |
испытаний, |
в каждом из |
которых |
событие |
может появиться, |
а может и не |
появиться. Испытания называются независимыми, если вероятность появления события в каждом из испытаний не зависит от того, появилось или не появилось
это событие в других испытаниях. Вероятность появления события в каждом
испытании одинакова и равна , а вероятность противоположного события
обозначим через |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
Теорема. |
Вероятность того, что в |
испытаниях событие |
появится ровно |
||||||||||||
|
|
= |
= 1 − |
|
|
|
|
|
|
|
|
|
||||
раз вычисляется по формуле Бернулли |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
P (k) Сk pk qn k , |
|
|
|
(1.16) |
||||
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
где |
вычисляется по формуле (1.2). Легко доказать, что Pn (k) 1. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
Замечание. Конечную |
серию |
|
повторных |
независимых |
испытаний с |
двумя |
||||||||||
исходами, вероятности которых равны |
и , называют схемой Бернулли. |
|
|
|||||||||||||
|
Наивероятнейшее |
число |
|
появления события |
в |
|
независимых |
|||||||||
испытаниях находится по формуле |
|
|
|
|
|
|
|
|
|
|||||||
|
− |
|
|
|
|
|
|
|
|
|
. |
|
− |
|
(1.17) |
|
Если |
- целое число, то |
наивероятнейших чисел ровно два: |
и |
+ |
. |
|||||||||||
|
|
|
− |
≤ |
≤ |
+ |
|
|
|
|
|
|
||||
Пример 1.15. Игральную кость подбрасывают 10 раз. Найти вероятность того,
что: а) шесть очков выпадет ровно 3 раза; б) шесть очков выпадет хотя бы один раз.
очков}. Тогда |
Введем событие, |
={в одном испытании. |
выпадет ровно шесть |
|||||||
Решение. |
( ) = = |
|
( |
|
) = = 1 − |
|
= |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
15 |
|
|
|
|
|
а) По формуле (1.16) вычисляем вероятность того, что шесть очков выпадет
ровно 3 раза из десяти |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
∙ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
вычисляем вероятность того, что шесть очков выпадет |
|||||||||||||
б) По формуле (1.13)(3) = |
∙ |
∙ |
= |
|
|
|
≈ 0 |
|
|
||||
Пример 1.16. В семье=5 |
1 − |
= 1 − |
= 0,8385 |
|
|||||||||
хотя бы один раз из десяти |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
детей. |
|
Вероятность рождения мальчика считаем |
||||||||||
равным 1/2. Найти вероятность того, что в семье ровно три мальчика. Какое наиболее вероятное количество мальчиков в семье?
Решение. Имеем = 5, = 1/2,3 3 |
2 |
=5!1/2.1Тогда3 1 |
2 |
10 |
|
||||||||
Р5 (3) С5 р q |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
3!2! |
|
2 |
|
|||||||||
|
|
|
|
2 |
|
|
32 |
|
|||||
По формуле (1.17) находим наивероятнейшее число мальчиков в семье из 5
детей
5 |
|
1 |
k |
|
|
5 |
|
1 |
, |
2 |
|
0 |
2 |
|
|||||
2 |
|
|
2 |
|
|||||
т.е. наивероятнейшее число равно 2 или 3.
Пример 1.17. Для нормальной работы автобазы на линии должно быть не менее 8 автомашин, а их имеется 10. Вероятность того, что автомашина на линию не выйдет равна 0,1. Найти вероятность нормальной работы автобазы в ближайший день.
Решение. Событие ={автобаза работает нормально}. Для нормальной работы автобазы на линии должно быть или 8 автомашин, или 9, или 10. Введем три события ={на линии работает 8 машин}, ={ на линии работает 9 машин}, ={ на линии работает 10 машин}. Тогда событие А можно представить в виде
объединения трех несовместных событий
=+ + .
= 0,1 , вычисляем |
|
|
|
|
, |
= 10, = 0,9, |
Используя формулу (1.16), и учитывая, что в нашем случае |
|
|||||
( |
) = |
(8) = |
0,9 |
0,1 |
= 0,1937, |
|
( |
) = |
(9) = |
0,9 |
0,1 |
= 0,3874 . |
|
( |
) = |
(10) = |
0,9 |
0,1 |
= 0,3487 |
|
|
|
16 |
|
|
|
|
Таким образом,
( ) = ( )+ ( ) + ( ) = 0,9298.
Локальная формула Лапласа
Пользоваться формулой Бернулли (1.16) при больших значениях достаточно
трудно. Например, для того, чтобы найти вероятность того, что при 30 испытаниях
герб выпадет 10 раз, необходимо вычислить |
|
(10) = |
|
|
|
|
|
|
|
|
|
. Первый |
|||||||||
|
|
( |
≥ 25) |
||||||||||||||||||
сомножитель требует громоздких вычислений. |
|
|
|
||||||||||||||||||
При большом числе опытов по схеме |
|
Бернулли |
удобнее |
||||||||||||||||||
пользоваться приближенными формулами. |
|
|
|
|
|
|
|
||||||||||||||
Локальная теорема Лапласа. Если |
|
|
|
|
, то вероятность того, что в |
||||||||||||||||
независимых испытаниях событие наступит |
раз, находится по формуле |
||||||||||||||||||||
≥ 10 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
P (k) |
|
1 |
|
х , |
|
|
|
|
|
|
|
|
|
|
|
(1.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n |
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k np |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где x |
|
|
|
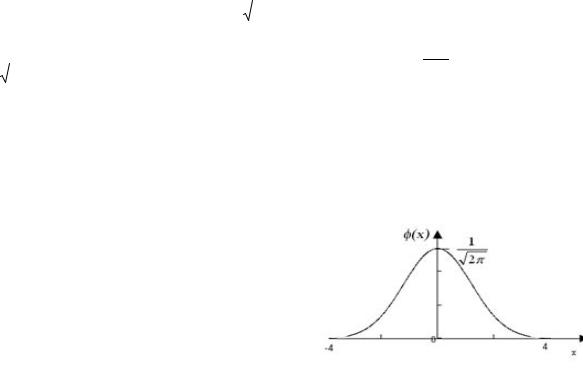
, а функция х определяется равенством ( ) = |
√ |
|
|
|
|
|
|
(рис.2.1). |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
npq |
|
|
|
|
|
|
|
|||||||||||||
Для облегчения вычислений функция х представлена в виде таблицы (см.
приложение 1).
Свойства функции Гаусса ( ).
1). Функция ( ) - четная, т.е. х = х .
2). lim х 0, можно считать х 0 для
x
всех значений ≥ 4.
3) (x)dx 1.
Рис.2.1. Функция Гаусса.
Пример 1.18. Найти вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, если вероятность поражения мишени при одном выстреле равна
0,4.
17
|
Решение. Поскольку |
|
|
- |
велико, |
и |
= 144 ≥ 10 |
, то вероятность |
|||||||
|
|
|
|
(1.18). |
|
|
|
|
|
|
|||||
будем вычислять по формуле = 600 |
|
|
|
|
|
|
|||||||||
|
Находим |
х |
250 600 0,4 |
|
|
10 |
0,833. |
По |
таблицам |
определяем |
|||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
600 0,4 0,6 |
|
|
12 |
|
|
|
|
|
|
0,833 0,2820. |
|
Тогда |
|
по |
локальной |
теореме |
Лапласа |
||||||||
Р600 |
(250) |
1 |
0,2820 0,0235. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула Пуассона (закон редких событий)
|
Теорема. |
Если |
|
и |
|
|
0 то вероятность того, |
что в |
||||
независимых |
|
событие |
наступит |
раз, находится по |
формуле |
|||||||
испытаниях< 10 |
|
< 0,1 (p |
|
|
), |
|||||||
Пуассона |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
Pn (k) |
|
k e |
, |
(1.19) |
|
|
|
|
|
|
|
|
|
k! |
||||
|
|
|
|
|
|
|
|
|
|
|
||
где |
- среднее число появлений события |
в |
испытаниях. |
|
||||||||
|
|
|||||||||||
|
Пример 1.19. Завод |
отправил |
на базу |
5000 |
доброкачественных |
изделий. |
||||||
Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что в пути будет повреждено: а) 3 изделия; б) не более 3-х изделий; в) более
3-х изделий.
и |
Решение. По условию, |
задачи. |
имеем = 5000, = 0,0002. Тогда |
|
= 0,9998 |
|
|
= 0,9998 < 10 |
< 0,1 |
|
e 1 |
|
|
|
а) = 3, = |
= 1, тогда по формуле (1.19) вычисляем P5000(3) |
|
0,0613. |
||
|
3! |
|||||
б) Введем событие В={в пути будет повреждено не более 3-х изделий}. Это событие равно объединению четырех несовместных событий {в пути повреждено ровно изделий}, где = 0,1,2,3. Тогда по формулам (1.7) и (1.19) имеем
( ) = ( ≤ 3) =P5000(0)+P5000(1)+P5000(2)+P5000(3)=
|
е 1 10 |
|
е 1 11 |
|
е 1 12 |
|
|
е 1 13 |
е 1(1 1 |
1 |
|
|
|
1 |
) е 1 2 |
2 |
е 1 |
8 |
0,9810. |
||||||
|
|
|
|
|
|
|
|
6 |
|
|
|||||||||||||||
0! |
1! |
2! |
3! |
|
2 |
|
|
|
3 |
3 |
|
|
|
||||||||||||
|
в) Противоположным событием к событию |
является следующее: |
|
={в пути |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
будет повреждено более 3-х изделий}. Тогда |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
= ( |
> 3) = 1 − ( |
|
) = 1 −0,9810 = 0,0190. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегральная теорема Муавра-Лапласа |
|
|||||||||
|
Если |
|
– большое и |
|
|
, то вероятность того, что событие |
произойдет |
||||||||||||
от |
раз до |
|
раз вычисляют≥по10интегральной формуле Муавра-Лапласа |
||||||||||||||||
|
|
|
|
|
|
|
|
|
Pn 1 к 2 Ф х2 Ф х1 , |
(1.20) |
|||||||||
где |
х k2 |
|
np , |
х k1 |
np |
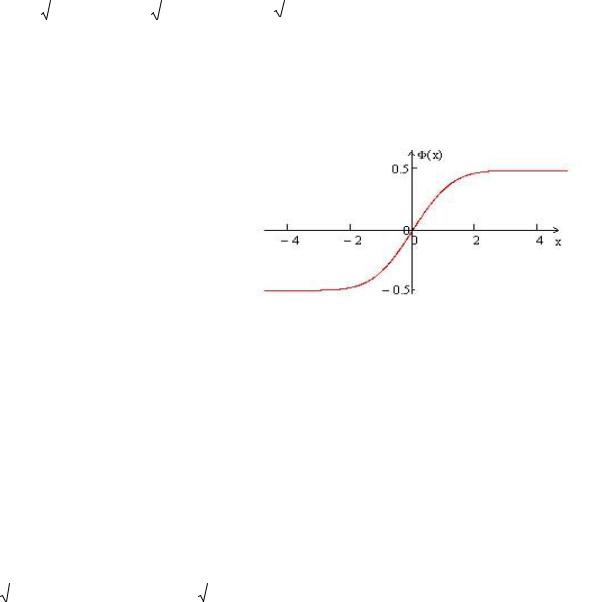
и Ф(х) 1 |
|
х |
|
t2 |
|
||||||||
|
|
e |
2 dt – функция Лапласа (рис.2.2). |
||||||||||||||||
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
npq |
|
npq |
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таблица значений функции Φ( ) приведена в приложении 2.
Свойства функции Лапласа
1)Φ( ) - нечетная функция, т.е. Φ(− ) = −Φ( ).
2)Φ( )–возрастающая функция на всей числовой оси.
3) limФ(х) 0,5, можно считать
x
Φ( ) ≈0,5, для всех значений ≥ 5.
Рис.2.2. Интегральная функция Лапласа.
|
|
|
Пример 1.21. Вероятность того, что деталь не прошла проверку ОТК, равна |
||||||||||||||||
р |
= 0,2 |
. Найти вероятность того, что среди 400 случайно отобранных деталей |
|||||||||||||||||
|
|
|
|
||||||||||||||||
окажется непроверенных от 70 до 100 деталей. |
|
|
|||||||||||||||||
|
|
|
Решение. При вычислении будем использовать формулу (1.20), |
||||||||||||||||
предварительно |
|
|
|
|
|
|
|
|
|
вычислив |
|
значения |
|||||||
х |
|
|
70 400 0,2 |
|
1,25, х |
2 |
|
100 400 0,2 |
|
2,5. |
По приложению 2 находим |
||||||||
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
400 0,2 0,8 |
|
|
|
|
400 0,2 0,8 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Φ |
(−1,25) = − (1,25) = −0,3944 |
, Φ |
(2,5) = 0,4938 |
. Тогда |
|||||||||||||||
|
|
|
|
Φ |
(70,100) = |
( |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
)− |
Φ |
( ) = Φ(2,5) +Φ(1,25) = 0,8882 |
||||||||||
|
|
|
|
|
|
|
|
|
Φ |
|
|
|
|
|
|
. |
|||
19
