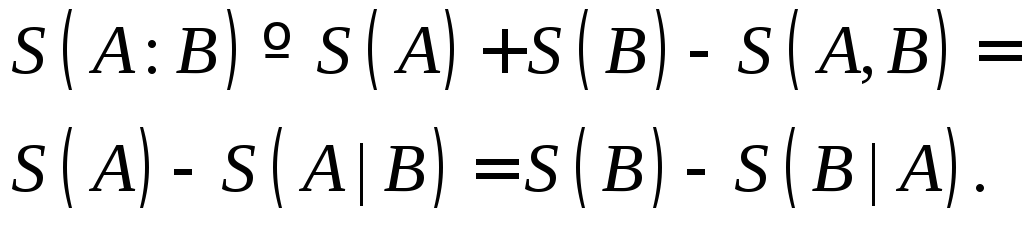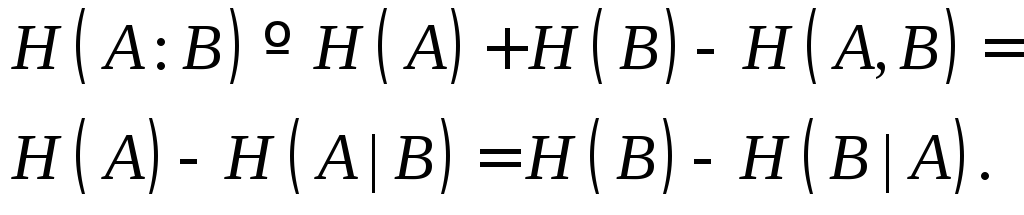- •Теории управления квантовыми системами.
- •Содержание
- •Введение
- •1. Основные понятия и определения квантовой механики
- •1.1. Чистые и смешанные состояния
- •1. 2. Обозначения Дирака
- •1. 3. Перепутанные состояния
- •2. Элементы квантовой теории информации
- •2. 1. Кубиты
- •2. 2. О квантовой информации
- •2. 3. Преобразование одного кубита
- •2. 4. Перепутывание
- •2.5. Перепутывание и квантовая неразличимость
- •2.6. Логический элемент «управляемое не»
- •3. Парадокс эйнштейна – подольского – розена (эпр)
- •4. Неравенства белла
- •5. Квантовая криптография
- •5.1. Понятие о криптографии
- •5.2. Ключи и их распределение
- •5.3. Открытые ключи
- •5.4 Понятие о квантовой криптографии
- •5.4.1. Защита посредством неортогональных состояний
- •5.4.2. Защита посредством перепутывания
- •5.4.3. Практическая реализация квантово – криптографических систем
- •6. Квантовая телепортация
- •6.1 Общие представления
- •6.2. Протокол квантовой телепортации
- •6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
- •6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
- •7. Квантовые вычисления. Квантовые компьютеры.
- •7.1. Вводные замечания
- •7.2. Квантовый регистр
- •7.3. Задачи поиска.
- •7.4. Квантовые алгоритмы
- •7.4.1. Моделирование времени.
- •7.4.2. Моделирование вероятности
- •7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
- •7.5. Общие требования к квантовым компьютерам Практическая реализация
- •Приложение. Гипотезы о квантовой природе сознания
- •Заключение
- •Словарь терминов
- •Литература
2. 2. О квантовой информации
Квантовая информация - новая область науки и технологии, сочетающая в себе разделы физики, математики, кибернетики и инженерии. Ее целью является выяснение роли фундаментальных законов физики, открытых в XX-ом веке, в процессах получения, передачи и обработки информации. Теория классической информации не может адекватно ответить на вопрос, как информация может быть использована в квантовом мире. Некоторые выводы теории квантовой информации могут быть представлены как обобщение классической теории в тех случаях, когда информация передается и хранится с помощью квантовых состояний, а не в терминах классических битов.
Квантовая теория информации устанавливает связь между мерой квантовой запутанности и информацией. Возможно, на фундаментальном уровне нет ничего, кроме квантовой информации, которая в процессе декогеренции проявляется в пространствах меньшей размерности в виде локальных объектов.
Целью квантовой теории информации является выявление общих принципов реализации квантовых вычислений и квантового компьютера. Важной задачей является отыскание новых способов обработки информации и исследование свойств сцепленных квантовых состояний.
Вычисление - это процесс, в ходе которого происходит определенное для каждой логической операции (ЛО) нелинейное взаимодействие потоков информации друг с другом и их преобразование. В зависимости от типа ЛО определенным образом изменяется состояние логического элемента (ЛЭ), а поступающая на его входы информация либо передается далее, либо как-то преобразуется. Управление или преобразование происходит под воздействием внешних сигналов. Это, например, переключение или инверсия (01, 10), запись, сброс. Носитель информации на физическом уровне называется сигналом.
Общеизвестно, что объекты микромира ведут себя совершенно необычно с точки зрения классического мира. Так, наблюдение за атомом возмущает его движение, в то же время в отсутствие наблюдения, атом как бы размыт по пространству и скоростям (отсутствие траектории, соотношение неопределенности Гейзенберга), как будто бы он находился в нескольких различных местах в одинаковые моменты времени.
Таким образом, до сих пор квантовые эффекты, связанные с малостью размеров различных устройств воспринимались как преграда на пути к миниатюризации электронных устройств. Квантовая информатика должна выяснить, как использовать фундаментальные квантовые свойства.
Один из основных вопросов теории информации заключается в том, какое количество информационного ресурса необходимо для выполнения данной задачи? Например, сколько шагов надо сделать для решения задачи факторизации, т.е. разложения простых сомножителей числа? Для простых сомножителей данного 300–значного числа классический алгоритм требует примерно 51024 шагов или около 150 тыс. лет при скорости вычислений порядка терагерц, а квантовый алгоритм требует 51010 шагов и выполняется меньше секунды при той же скорости.
Б. Шумахер выделяет такие элементы информатики:
1. Выбрать физические ресурсы, например, строку битов, действительно рассматриваемых не абстрактно, а как физическую систему.
2. Сформулировать задачу обработки информации, выполняемую с помощью физического ресурса.
3. Выбрать критерий успешного выполнения задачи.
Итак, главный вопрос теории информации таков: какова минимальная величина физического ресурса для выполнения задачи обработки информации в соответствии с критерием успеха?
В квантовой теории информации эти процедуры приобретают специфические черты: в качестве физического ресурса здесь выступают сцепленные состояния, при обработке информации необходимо управлять ими, а критерий успеха менее определён и очевиден, чем в классическом случае.
Одним из приложений квантовой информатики является криптография. Здесь уже разработаны и реализованы алгоритмы, использующие такие свойства квантовых объектов, как неклонируемость и невозможность измерения (перехвата сообщения) без возмущения. Основной выигрыш в квантовых криптографических протоколах - даже не абсолютная их секретность, а то, что сам факт подслушивания становится известным для пользователей, т.к. любое вторжение в квантовую систему с неизбежностью изменит её состояние, что сразу станет известно субъектам, обменивающихся информацией.
Итак, Проблема 1 -уменьшение размеров интегральных схем, т.е. отдельных элементов. Естественный предел здесь - характерный масштаб атома, когда вступают в силу законы микромира, т.е. квантовой механики. Проблема 2- уменьшение доли рассеиваемой энергии. Логически обратимые операции - те, которые не сопровождаются рассеянием энергии (Ландауер, 1961г.). Универсальный цифровой компьютер типа вычислительной машины Тьюринга может быть построен на логически и термодинамически обратимых ЛЭ так, что энергия будет рассеиваться только за счет необратимых периферийных процессов (типа ввода информации в машину либо ее вывода).
Для выполнения классических вычислений необходима физическая система, имеющая два устойчивых состояния, например, триггеры - в радиоэлектронике.
Квантовый же компьютер - физическое устройство, выполняющее логические операции над квантовыми состояниями путем унитарных преобразований, не нарушающих квантовые суперпозиции в процессе вычислений. Схематично, работа квантового компьютера может быть представлена как последовательность трех операций:
“ЗАПИСЬ” (приготовление начального состояния),
“ВЫЧИСЛЕНИЕ” (унитарные преобразования начальных состояний)
“ВЫВОД” результата (измерение, проецирование конечного состояния).
Также сюда следует отнести вспомогательную операцию “СБРОС”, приводящую регистр к основному состоянию.
Рассмотрим связь информации и энтропии. Пусть имеется лента, разбитая на ячейки - классический регистр. Если в каждой ячейке может быть помещен только один из двух символов, то говорят, что в ячейке содержится бит информации. Очевидно, что в регистре, содержащем N ячеек содержится N бит информации и в нем можно записать 2N сообщений. Итак, информационная энтропия измеряется в битах:
![]() (2.9)
(2.9)
Здесь QN = 2N - полное число различных сообщений. Из (2.9) ясно, что информационная энтропия равна минимальному числу двоичных ячеек, с помощью которых можно записать некую информацию.
Определение (2.9) можно переписать по-другому. Пусть у нас имеется множество QN различных сообщений. Найдем вероятность того, что необходимое нам сообщение совпадет со случайно выбранным из общего числа QN различных сообщений. Она равна, очевидно, PN = 1/QN. Тогда определение (2.9) запишется как:
![]() (2.10)
(2.10)
Чем больше число ячеек N, тем меньше вероятность PN и тем больше информационная энтропия HB, содержащейся в данном конкретном сообщении.
Например, число букв алфавита равно 32 (без буквы ё), т.е. 25. Чтобы каждой букве сопоставить определенную комбинацию двоичных чисел необходимо иметь 5 ячеек. Добавив к строчным буквам заглавные, мы удваиваем число символов, которые хотим закодировать - их станет 64 = 26 - т.е. добавляется лишний бит информации HB = 6. Здесь HB - объем информации, приходящийся на одну букву (строчную или заглавную). Однако такой прямой подсчет информационной энтропии не совсем точен, поскольку в алфавите есть буквы, которые встречаются реже или чаще. Тем буквам, которые встречаются реже, можно отдать б'ольшее количество ячеек, а на часто встречающихся буквах - сэкономить и отдать им те состояния регистра, которые занимают меньшее количество ячеек. Точное определение информационной энтропии было дано Шенноном:
![]() (2.11)
(2.11)
Для рассмотренного примера суммирование ведется по всем символам (буквам алфавита), а pi означает вероятность появления символа с номером i. Как видно, это выражение охватывает как часто используемые буквы, так и буквы, вероятность появления которых в данном сообщении мала.
Поскольку в выражении (2.11) используется натуральный логарифм, соответствующую единицу информации называют “нат”.
Информационная энтропия - это мера недостатка (или степень неопределенности) информации о действительном состоянии физической системы.
Информационная энтропия Шеннона:
![]() ,
,
где
![]()
Это относится к двухуровневым системам, типа бит: “0” и “1”. Если размерность равна n, то H = logn.
Так, для n = 3, Н = log3, причем, = 3.
Количество информации I (или просто информация) о состоянии классической системы, получаемое в результате измерений внешним прибором, связанным с рассматриваемой системой некоторым каналом связи, определяется как разность информационной энтропии, соответствующей начальной неопределенности состояния системы H0, и информационной энтропии конечного состояния системы после измерения H. Таким образом,
I + H = H0 = const.
В идеальном случае, когда отсутствуют шумы и помехи, создаваемые внешними источниками в канале связи, конечное распределение вероятностей после измерения сводится к одному определенному значению pn = 1, т.е. H = 0, а максимальное значение полученной при измерении информации будет определяться : Imax = H0. Таким образом, информационная энтропия Шеннона системы имеет смысл максимальной информации, заключенной в системе; она может быть определена в идеальных условиях измерения состояния системы в отсутствие шумов и помех, когда энтропия конечного состояния равна нулю, H = 0.
Рассмотрим классический логический элемент, который может находиться в одном из двух равновероятных логических состояний “0” и “1”. Переход элемента в одно из состояний, например, в состояние “0”, соответствует уменьшению статистического веса его состояния по сравнению с начальным состоянием в 2 раза (для трехуровневых систем - в 3 раза). Найдем уменьшение информационной энтропии Шеннона, которое соответствует увеличению количества информации об элементе на один бит:
Следовательно, информационная энтропия определяет число битов, которое требуется для кодирования информации в рассматриваемой системе или сообщении.
При обобщении
энтропии Шеннона на квантовый случай
(энтропию фон Неймана) необходимо
определить оператор энтропии через
оператор плотности
![]() :
:
S=
- ln
![]()
Тогда, очевидно, физическая величина “энтропия” или S есть среднее значение этого оператора или по правилам вычисления средних величин в квантовой механике:
S=
-
![]() ln
ln
![]()
![]() =
- Sp(
=
- Sp(![]() ln
ln
![]() )
)
Для рассмотрения процедуры вычисления логарифма оператора (недиагональные элементы матрицы плотности - вообще могут быть комплексными величинами, для которых логарифм не определен) рассмотрим две ситуации.
Чистое состояние. В этом случае возможно описание квантовой системы с помощью волновой функции в базисном представлении (т.е. как когерентную суперпозицию базисных состояний какого-нибудь оператора):
![]() .
.
В этом случае,
конечно, матрица плотности недиагональна.
Наличие недиагональных элементов в
базисном представлении как раз и отражает
факт когерентности суперпозиции базисных
состояний. Вообще же матрица плотности
любой физической системы должна быть
положительно определена, т.е. все ее
собственные значения должны лежать в
интервале [0,1]. Из линейной алгебры
известно, что для любой эрмитовой матрицы
А существует такая невырожденная матрица
Т, что матрица
![]() является диагональной.
Диагональные элементы матрицы
является диагональной.
Диагональные элементы матрицы
![]() в этом случае действительные и являются
собственными значениями матрицыА.
Более того, существует такая невырожденная
матрица Т,
что диагональные элементы
в этом случае действительные и являются
собственными значениями матрицыА.
Более того, существует такая невырожденная
матрица Т,
что диагональные элементы
![]() - принимают только значения +1, -1 и/или
0.
- принимают только значения +1, -1 и/или
0.
Физически, матричное
унитарное преобразование
![]() означает смену представления или базиса.
Таким образом, чистое состояние системы
всегда может быть представлено в виде
собственного состояния какого-нибудь
оператора. Например, рассмотрим
когерентную суперпозицию двух состояний
или кубит:
означает смену представления или базиса.
Таким образом, чистое состояние системы
всегда может быть представлено в виде
собственного состояния какого-нибудь
оператора. Например, рассмотрим
когерентную суперпозицию двух состояний
или кубит:
![]()
Пусть![]() .
Полным аналогом такого состояния
является состояние поляризации света,
когда поляризация составляет угол 450
с вертикалью. Действительно, измерения
поляризации отдельных фотонов в этом
состоянии будут давать либо горизонтальную,
либо вертикальную поляризации с
вероятностью 1/2. В то же время измерения,
проводимые в базисе +450,всегда
будут давать достоверный результат.
.
Полным аналогом такого состояния
является состояние поляризации света,
когда поляризация составляет угол 450
с вертикалью. Действительно, измерения
поляризации отдельных фотонов в этом
состоянии будут давать либо горизонтальную,
либо вертикальную поляризации с
вероятностью 1/2. В то же время измерения,
проводимые в базисе +450,всегда
будут давать достоверный результат.
Эти рассуждения можно обобщить на случай произвольной (эллиптической) поляризации, когда в разложении волновой функции отличны от нуля два комплексных коэффициента.
Энтропия фон Неймана, определяемая через матрицу плотности, инвариантна относительно выбора базиса или представления, т.е., переходя к диагональному представлению,
![]() . (2.12)
. (2.12)
Но в чистом состоянии
лишь один элемент матрицы плотности
отличен от нуля, т.е.
![]() ,
а значит S
= 0. Равенство нулю энтропии интерпретируется
как минимальная неопределенность
(хаотичность).
,
а значит S
= 0. Равенство нулю энтропии интерпретируется
как минимальная неопределенность
(хаотичность).
2. Смешанное
состояние.
Рассмотрим однородную смесь состояний:
![]() где, как обычно,Г
- число состояний с данной энергией,
т.е. микроканонический ансамбль Гиббса.
где, как обычно,Г
- число состояний с данной энергией,
т.е. микроканонический ансамбль Гиббса.
В
смешанном состоянии недиагональные
элементы матрицы плотности равны нулю
- матрица имеет диагональный вид с
диагональными элементами
![]() .
Матрицу плотности смешанного состояния
всегда можно привести к диагональному
виду, но по диагонали будут стоять
классические вероятности p1......pn.
.
Матрицу плотности смешанного состояния
всегда можно привести к диагональному
виду, но по диагонали будут стоять
классические вероятности p1......pn.
Известно, что в диагональном представлении функции от операторов удовлетворяют соотношению:
![]() ,
,
где функционал F в данном случае - логарифм.
Тогда,
![]() ,
,![]()
и из (2.12) следует, что
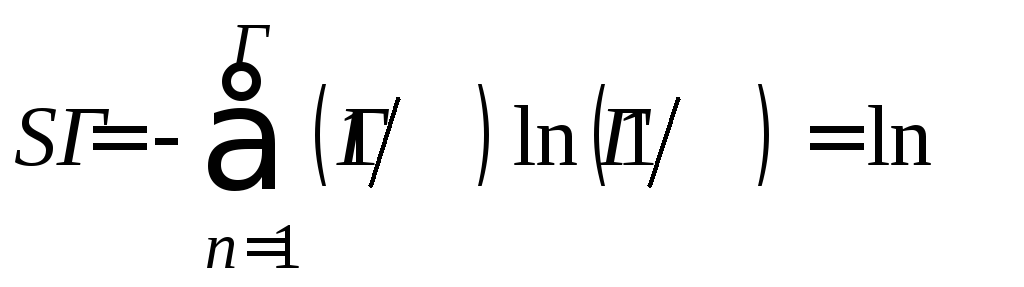 .
.
Отсюда видно, что
выполняется неравенство
![]() .
.
Рассмотрим двухуровневую систему
![]() . (2.13)
. (2.13)
Такой волновой функцией описываются, например, электронные или ядерные спины, двухуровневые атомы и прочее, иначе, это - кубит. Пусть основному состоянию атома приписывается значение собственного вектора |0>, а возбужденному - собственный вектор |1> (или значение проекции на ось z спина). Эти векторы в квантовой механике записываются в виде столбцов
![]()
Собственные “бра” векторы <| образуют эрмитово-сопряженные строки:
![]() .
Вектор состояния оканчивается на
окружности единичного радиуса в двумерном
гильбертовом пространстве. Измерение
такого состояния состоит в определении
коэффициентов разложения, или проекций
измеряемого состояния на базисные
состояния:
.
Вектор состояния оканчивается на
окружности единичного радиуса в двумерном
гильбертовом пространстве. Измерение
такого состояния состоит в определении
коэффициентов разложения, или проекций
измеряемого состояния на базисные
состояния:
![]()
Собственному представлению оператора плотности двухуровневой системы, находящейся в чистом состоянии, соответствует диагональная матрица, выраженная через собственные векторы
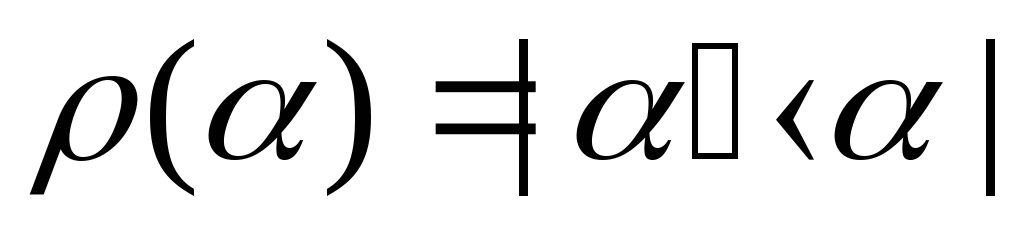 ,
,
причем двум возможным (собственным) состояниям отвечают следующие матрицы плотности:
![]() .
Т.о. для каждого
= 0, 1 у двухуровневой системы, находящейся
в чистом состоянии, имеется только одно
ненулевое значение матрицы, равное 1.
.
Т.о. для каждого
= 0, 1 у двухуровневой системы, находящейся
в чистом состоянии, имеется только одно
ненулевое значение матрицы, равное 1.
Для смешанного состояния и выбранного базиса матрица плотности имеет диагональный вид, поскольку недиагональные элементы, отвечающие за “когерентность” суперпозиции (2.13) равны нулю:
![]() ,
,
![]()
Отсюда сразу
следует, что энтропия S
совпадает с классической энтропией
Шеннона случайной величины
![]() .
Забегая вперед, можно сказать, что
энтропия фон Неймана совпадает с
энтропией Шеннона.
.
Забегая вперед, можно сказать, что
энтропия фон Неймана совпадает с
энтропией Шеннона.
Рассмотрим когерентную суперпозицию (2.13). Тогда вектор ее состояния:

Матрица плотности чистого состояния уже недиагональна и в базисном представлении имеет вид:
 (2.14)
(2.14)
Собственные
значения матрицы
находятся по правилу: пусть А
- квадратная матрица
![]() ,
тогда любой векторх,
из пространства Vn
для которого выполняется Ах=х
называется собственным вектором, а
- собственным значением матрицы. Это
уравнение эквивалентно уравнению
(A-I)х
= 0. Это
однородная система линейных уравнений.
Нетривиальные решения имеются тогда,
когда определитель равен нулю:
,
тогда любой векторх,
из пространства Vn
для которого выполняется Ах=х
называется собственным вектором, а
- собственным значением матрицы. Это
уравнение эквивалентно уравнению
(A-I)х
= 0. Это
однородная система линейных уравнений.
Нетривиальные решения имеются тогда,
когда определитель равен нулю:
det(A-I) = 0.
Или
![]() .
.
Составим уравнение для собственных значений матрицы (2.14):

и, тогда
![]() .
.
Найдем энтропию
Шеннона чистого состояния суперпозиции
(2.13). Она совпадает с энтропией смешанного
состояния с заданными классическими
вероятностями заполнения или населенностями
![]() ,
поскольку не учитывает вклада
недиагональных членов
,
поскольку не учитывает вклада
недиагональных членов![]()
Итак, энтропия Шеннона:
![]() .
.
Максимальное
значение эта величина достигает при
![]() ,
когда
,
когда![]() .
.
Отметим, что отличие матрицы плотности чистого состояния от смешанного состоит в том, что матрица плотности чистого состояния имеет только одно собственное значение, равное единице, в то время как для смешанного состояния у матрицы плотности отличны от нуля несколько собственных значений - т.н. парциальные (т.е. взвешенные с классическими вероятностями) населенности соответствующих чистых состояний.
Энтропия фон Неймана, определяемая через матрицу плотности, согласно (2.12), в отличие от энтропии Шеннона, инвариантна относительно выбора представления матрицы плотности. Из (2.12) видно, что
![]() .
.
Итак, классическая
(шенноновская) энтропия дает меру
неопределенности, связанную с классическим
распределением вероятностей. Квантовые
состояния описываются схожим образом,
только вместо распределения вероятностей
используются операторы плотности:
![]() В
теории информации логарифмы принято
брать по основанию “2”, в отличие от
статистической физике, где используется
по основанию “е” - “наты”.
В
теории информации логарифмы принято
брать по основанию “2”, в отличие от
статистической физике, где используется
по основанию “е” - “наты”.
Как и для энтропии Шеннона, полезно ввести квантовый аналог относительной энтропии. Пусть r и s -два оператора плотности. Относительной энтропией состояний (операторов) r и s (r относительно s) называется величина:
![]()
Как и соответствующая классическая величина, квантовая относительная энтропия может принимать бесконечные значения.
Так, относительная энтропия определяется как бесконечная, если ядро (kernel) оператора s (векторное пространство собственных векторов s с нулевыми собственными значениями) имеет нетривиальное пересечение с основанием (support) оператора r (векторное пространство образованное собственными векторами r с ненулевыми собственными значениями). В других случаях относительная энтропия конечна.
Квантовая относительная энтропия неотрицательна (неравенство Клейна):
![]()
равенство достигается, когда r = s.
Основные свойства энтропии фон Неймана.
Энтропия неотрицательна. Она принимает нулевые значения только для чистых состояний.
В N-мерном гильбертовом пространстве максимальное значение энтропии logN. Энтропия равна logN только если система находится в (полностью) смешанном состоянии I/d.
Предположим, что композиционная система AB находится в чистом состоянии. Тогда
S(A) = S(B)
Предположим, что pi - это вероятности, а состояния ri - раскладывается по собственным векторам с ненулевыми собственными значениями (имеют основание) в ортогональном базисе. Тогда
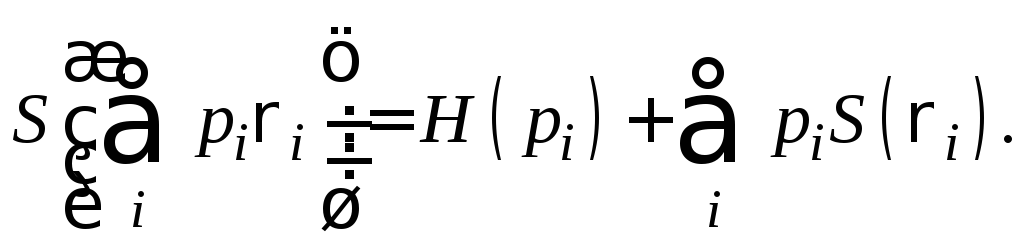
Теорема о совместной энтропии: предположим, что pi - вероятности,
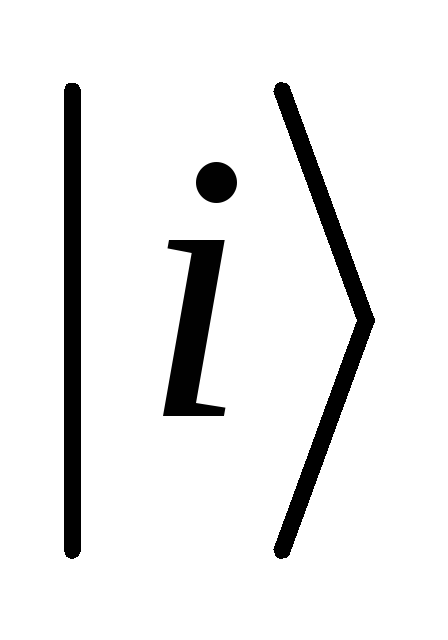 - ортогональные состояния для системыА
и ri
- любой набор операторов плотности для
другой системы В,
Тогда
- ортогональные состояния для системыА
и ri
- любой набор операторов плотности для
другой системы В,
Тогда
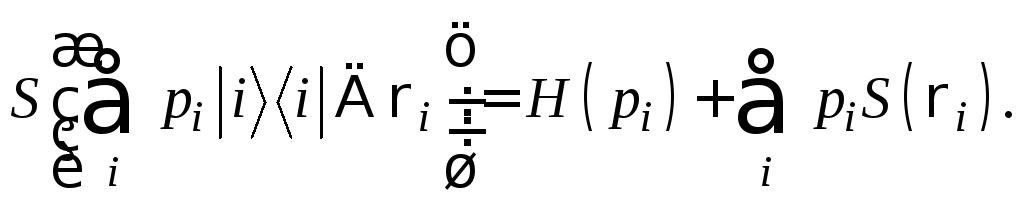
Субаддитивность энтропии . Пусть различные квантовые системы А и В имеют общее состояние rАВ. Тогда совместная энтропия для двух систем удовлетворяет следующим неравенствам:
![]() ,
причем равенство имеет место только
если системы А и В некоррелированы, т.е.
,
причем равенство имеет место только
если системы А и В некоррелированы, т.е.
![]()
![]() - т.н. неравенство
треугольника или Араки-Льеба. Это,
фактически, квантовый аналог неравенства
- т.н. неравенство
треугольника или Араки-Льеба. Это,
фактически, квантовый аналог неравенства
![]() для энтропии Шеннона.
для энтропии Шеннона.
Вогнутость энтропии. Пусть pi - неотрицательные действительные числа, такие, что
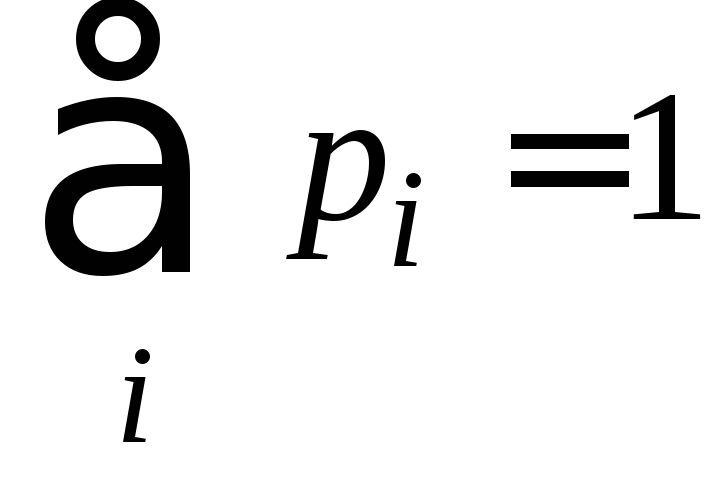 ,
аri
- соответствующие операторы плотности.
Тогда энтропия удовлетворяет неравенству:
,
аri
- соответствующие операторы плотности.
Тогда энтропия удовлетворяет неравенству:
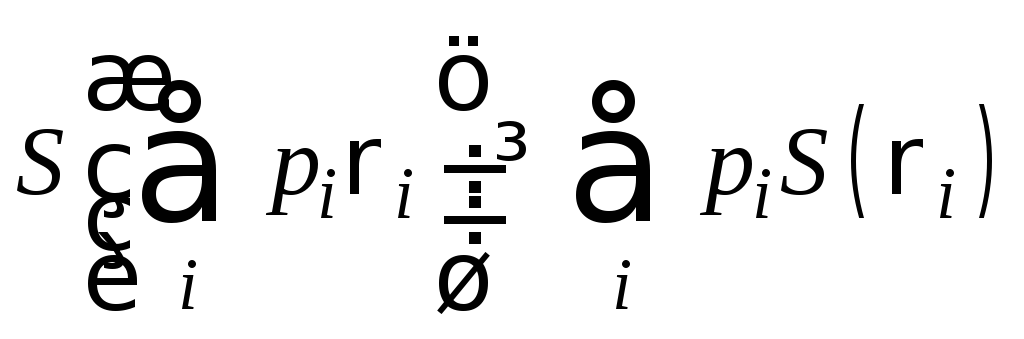 - следует из св-ва
(4).
- следует из св-ва
(4).
Интуитивно ясно,
что
![]() выражает состояние квантовой системы,
которая находится в неизвестном состоянииri
с вероятностью
pi.
Неопределенность нашего знания о такой
смеси состояний должна быть больше, чем
средняя неопределенность состояний
ri,
поскольку
состояние
выражает состояние квантовой системы,
которая находится в неизвестном состоянииri
с вероятностью
pi.
Неопределенность нашего знания о такой
смеси состояний должна быть больше, чем
средняя неопределенность состояний
ri,
поскольку
состояние
![]() дает вклад в неопределенность не только
из-за наличия состоянийri
но и благодаря
усреднению по индексу i.
дает вклад в неопределенность не только
из-за наличия состоянийri
но и благодаря
усреднению по индексу i.
Энтропия смеси квантовых состояний. Обратная сторона условия вогнутости проявляется в некоей полезной теореме, дающей верхнюю границу для энтропии смеси квантовых состояний. А именно, что для смеси
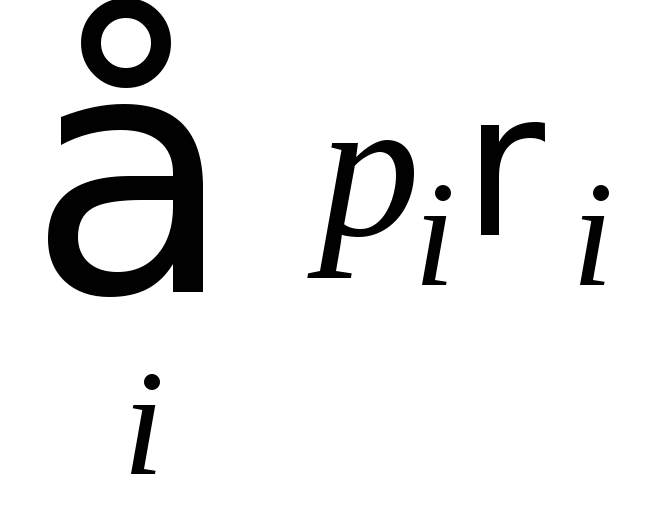 квантовых состоянийri
выполняется
следующее неравенство:
квантовых состоянийri
выполняется
следующее неравенство:
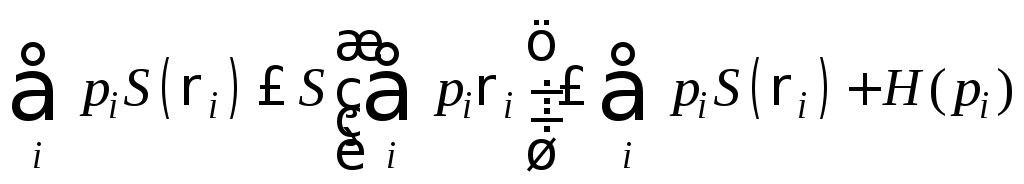
Что можно сказать
о верхней границе или о правой части
неравенства? Интуитивно ясно, что
неопределенность состояния
![]() не
может быть больше, чем средняя
неопределенность состоянияri
плюс
дополнительный вклад за счет H(pi),
который представляет собой максимально
возможный вклад в неопределенность об
индексе i
в общую неопределенность Сформулируем
теперь теорему о верхней границе
не
может быть больше, чем средняя
неопределенность состоянияri
плюс
дополнительный вклад за счет H(pi),
который представляет собой максимально
возможный вклад в неопределенность об
индексе i
в общую неопределенность Сформулируем
теперь теорему о верхней границе
Теорема.
Предположим, что
![]() ,
гдеpi
- некоторый набор вероятностей, а ri
- операторы плотности. Тогда
,
гдеpi
- некоторый набор вероятностей, а ri
- операторы плотности. Тогда
![]() ,
(**)
,
(**)
причем равенство достигается, если состояния ri образуют ортогональный набор.
По аналогии с классическим случаем (энтропия Шеннона) для композиционных систем можно определить квантовые совместную и условную энтропии, а также квантовую взаимную информацию. Совместная энтропия S(A, B) для композиционной системы, состоящей из двух компонент А и В, определяется как и в классике:
![]() (2.14)
(2.14)
где
![]() - матрица плотности системыАВ.
- матрица плотности системыАВ.
В классическом случае условной энтропией называлась величина
![]() ,
(2.15)
,
(2.15)
где во втором равенстве использовано понятие совместной вероятности
![]() - есть вероятность
того, что Х
принимает значение
х, а Y
принимает значение y.
- есть вероятность
того, что Х
принимает значение
х, а Y
принимает значение y.
Из определения (2.15) следует, что S(Y|X) есть мера того, сколько информации, в среднем, оставалось бы в Y при условии, что было бы известно Х. Заметим, что всегда S(Y|X) £ S(Y) и обычно S(Y|X) ¹ S(Х|У).
Определим условную энтропию, как
![]() (2.16)
(2.16)
Определим взаимную информацию, как
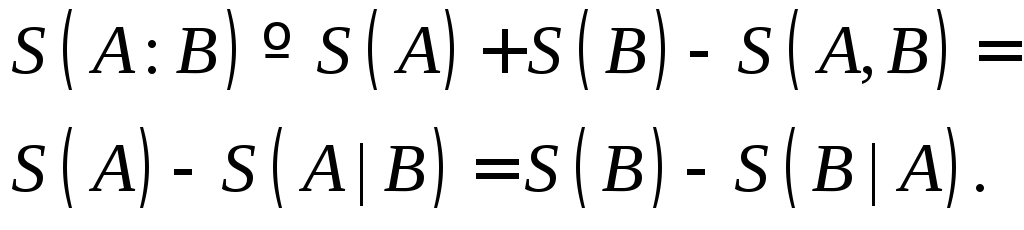 (2.17)
(2.17)
Некоторые свойства энтропии Шеннона не переносятся на энтропию фон Неймана и отсюда следуют интересные следствия квантовой теории информации. Например, для случайных переменных X и Y имеет место неравенство: H(X) £ H(X, Y). Интуитивно, это понятно: не может быть большей неопределенности состояния X, чем для совместного состояния X и Y. Это интуитивное понимание не годится для квантовых состояний. Рассмотрим систему АВ двух кубитов в перепутанном состоянии :
![]() .
(2.18)
.
(2.18)
Это чистое состояние,
поэтому S(A,
B)
= 0. С другой
стороны, система А
имеет оператор плотности I/2
(I
- единичный оператор) и поэтому ее
энтропия равна единице. Действительно,
волновой функции состояния системы А
(или В)
(2.18) не существует, это состояние
максимально смешанное. Другой способ
интерпретации этого результата состоит
в том, что для этой системы величина
(условная энтропия)
![]() - отрицательная. Это соотношение может
трактоваться как критерий перепутывания:
если |АВ>
- чистое состояние композиционной
системы, то |АВ>
находится в перепутанном состоянии
если и только если S(A|B)
< 0.
- отрицательная. Это соотношение может
трактоваться как критерий перепутывания:
если |АВ>
- чистое состояние композиционной
системы, то |АВ>
находится в перепутанном состоянии
если и только если S(A|B)
< 0.
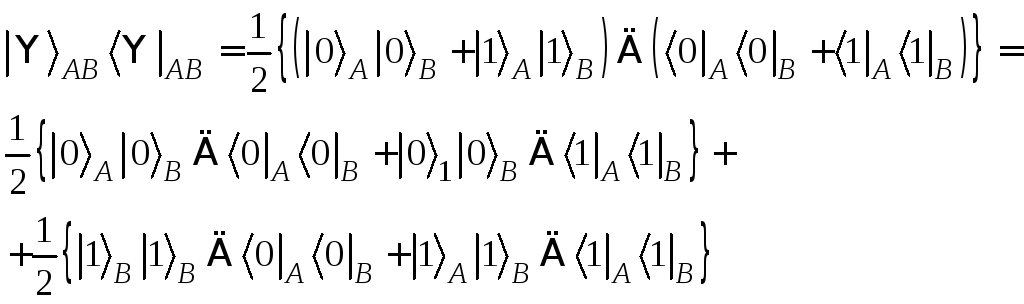
Тогда матрица плотности второй подсистемы
![]() ,
,
т.е. представляет собой взвешенную смесь. Следовательно, состояние второй подсистемы нельзя описывать волновой функцией; оно не является полностью определенным. Аналогично, матрица плотности первой подсистемы находится как след по индексам второй подсистемы:
![]() .
.
Классическая теория информации, в основном, затрагивает проблему пересылки классических сообщений - букв алфавита, текстов, строк битов - через каналы связи, которые работают в соответствии с законами классической физики. Как изменится картина, если будут использоваться квантовые каналы связи? Можно ли передать информацию более эффективно? Можно ли использовать законы квантовой механики для того, чтобы передавать секретную информацию, защищенную от подслушивания? Такого рода вопросы возникают, когда мы используем каналы связи, работающие по законам квантовой механики. Такое переопределение того, что же есть канал связи вызвано необходимостью переосмысления основных положений классической теории информации .
Квантовая теория информации нацелена на исследование каналов связи, но она имеет гораздо более широкую область применения. Можно обозначить три фундаментальные цели, которые стоят перед теорией квантовой информации:
идентифицировать элементарные классы статических ресурсов в квантовой механике (или типы “информации”)
идентифицировать элементарные классы динамических процессов в квантовой механике (или типы информационных процессов)
характеризовать ресурсы, с помощью которых можно реализовать элементарные динамические процессы.
Оказывается, что квантовая теория информации гораздо глубже и богаче классической теории информации потому, что квантовая механика включает в себя гораздо больше элементарных классов статических и динамических ресурсов, которые не просто соответствуют известным классическим типам, но и описывают целые новые типы состояний, например, перепутанные состояния, которые не имеют аналога в классической физике.
Рассмотрим на некоторых примерах разницу в описании между квантовой и классической информацией.
По принципу соответствия “законы квантовой физики должны быть сформулированы таким образом, что в классических границах, когда в процесс вовлечено много квантов, эти законы приводили бы к классическим уравнениям для усредненных величин.” (Д.Бом).
Предположим, что Алиса имеет классический источник информации, который выдает символы X = 0, ... n с соответствующим распределением вероятностей p0, ..., pn. Цель Алисы и Боба состоит в том, чтобы Боб смог определить величину X наилучшим образом. Для того, чтобы достигнуть этого, Алиса приготавливает квантовое состояние rХ выбирая его из некоторого фиксированного набора r0,.... rn, и посылает это состояние Бобу, который выполняет квантовое измерение над этим состоянием. Затем, он пытается сделать лучшее предположение о том, как идентифицировать X, основываясь над результатах своих измерений Y.
Хорошей мерой того, сколько информации получено Бобом о величине X из его измерений - это взаимная информация между X и результатом измерения Y. Боб может сделать заключение об X по результатам измерения Y только, если и только если H(X:Y) = H(X), и что в общем случае H(X:Y) £ H(X). Близость величины H(X:Y) к H(X) не самом деле дает хорошую меру того, как Боб смог определить Х. Цель Боба - выбрать измерение, которое максимизирует величину H(X:Y) и тем самым приближает ее к H(X). Для этого, определим достижимую информацию, как максимальную величину взаимной информации. Достижимая информация - это мера того, насколько хорошо Боб смог сделать вывод о приготовленном Алисой состоянии, которая она послала ему. Проиллюстрируем эти расссужденияследующим рисунком и сравнительной таблицей.

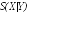
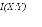
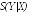



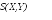
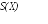
|
Квантовая информация |
Классическая информация |
|
Условная энтропия:
МОЖЕТ БЫТЬ ОТРИЦАТЕЛЬНОЙ |
Условная энтропия:
H(B|A) £ H(B) |
|
Совместная энтропия:
|
Совместная энтропия: H(B) £ H(B|A) |
|
Взаимная информация:
|
Взаимная информация:
|
В теории классической
информации, достижимая информация не
так интересна. Если на практике различение
пары классических состояний может
встретить определенные трудности, то
в принципе, это всегда можно проделать.
В отличие от этого, в квантовом случае,
далеко не всегда возможно различить
два состояния даже в принципе. Например,
не существует однозначной процедуры,
позволяющей различить два неортогональных
состояния. Будем “выражаться” в терминах
достижимой информации. Если Алиса
готовит состояние
![]() с вероятностьюp
и другое неортогональное состояние
с вероятностьюp
и другое неортогональное состояние
![]() с вероятностью1
- p,
то достижимая информация при таком
приготовлении уж точно меньше, чем
H(p),
поскольку Боб не может определить
принадлежность состояния с полной
достоверностью. В классическом случае,
если Алиса готовит два классических
состояния, например, бит - в состоянии
“0” с вероятностью
p
или “1” с
вероятностью 1
- p,
то не существует фундаментального
закона, запрещающего Бобу различить
эти состояния, поэтому достижимая
информация оказывается такой же как и
энтропия приготовления, т.е. H(p).
с вероятностью1
- p,
то достижимая информация при таком
приготовлении уж точно меньше, чем
H(p),
поскольку Боб не может определить
принадлежность состояния с полной
достоверностью. В классическом случае,
если Алиса готовит два классических
состояния, например, бит - в состоянии
“0” с вероятностью
p
или “1” с
вероятностью 1
- p,
то не существует фундаментального
закона, запрещающего Бобу различить
эти состояния, поэтому достижимая
информация оказывается такой же как и
энтропия приготовления, т.е. H(p).
Существует важное замечание, относящееся к этой дискуссии - когда концепция достижимой информации имеет классический смысл. Суть его - в различении распределений вероятностей. Представим, что Алиса готовит состояние “0” или “1” с двумя распределениями вероятностей либо с (p, 1 - p) либо с (q, 1 - q). Получая состояние Боб должен определить, какое распределение вероятности использовала Алиса для приготовления состояния. Очевидно, что Боб не всегда способен определить это с достоверностью 100%. Тем не менее, этот пример (по аналогии с достижимой информацией для квантовой системы, приготавливаемой в одном состоянии из набора смешанных состояний) очень важен. Что является наиболее важным и замечательным - так это то, что фундаментальные объекты в квантовой механике - чистые квантовые состояния - обладают свойствами различимости, что является существенно отличным и существенно богатым свойством, нежели чем для фундаментальных объектов классической теории информации, таких как “0” и “1”.
Теорема о запрете клонирования сулит другую перспективу в плане ограничения на достижимую квантовую информацию по сравнению с классической. Классическая информация, безусловно, может быть копирована. Это точно можно сделать с цифровой информацией, например, создавая копии файлов с текстами, заложенными в компьютер. Теорема о запрете клонирования утверждает, что квантовая механика не позволяет точно копировать неизвестное квантовое состояние и накладывает некоторые ограничения на возможность создания примерных копий.
На первый взгляд,
теорема о запрете клонирования выглядит
довольно странно. В конце концов, не
является ли классическая физика частным
случаем квантовой механики? Почему мы
можем копировать классическую информацию,
если нельзя копировать квантовую? Ответ
состоит в том, что эта теорема не запрещает
копировать все квантовые состояния.
Она лишь утверждает, что нельзя копировать
неортогональные квантовые состояния.
Далее, теорема подразумевает, что
невозможно построить квантовый прибор
так, чтобы при наличии на входе состояний
![]() и
и![]() ,
на выходе будет две копии входного
состояния
,
на выходе будет две копии входного
состояния![]()
![]() или
или![]()
![]() .
С другой стороны, если
.
С другой стороны, если![]() и
и![]() ортогональны, то теорема не запрещает
их копирование. Действительно, довольно
просто сконструировать квантовые схемы,
которые копируют такие состояния. Это
замечание разрешает кажущееся противоречие
между теоремой о запрете клонирования
и способностью копировать классическую
информацию. Для различных состояний
классическая информация может
восприниматься как представляемая
ортогональными состояниями.
ортогональны, то теорема не запрещает
их копирование. Действительно, довольно
просто сконструировать квантовые схемы,
которые копируют такие состояния. Это
замечание разрешает кажущееся противоречие
между теоремой о запрете клонирования
и способностью копировать классическую
информацию. Для различных состояний
классическая информация может
восприниматься как представляемая
ортогональными состояниями.
Теорема о запрете клонирования
Предположим, что
у нас есть квантовое устройство с двумя
портами А
и В.
Порт А
- это порт
данных. В
него помещается неизвестное, но чистое
квантовое состояние
![]() .
Это состояние требуется скопировать
на порте-мишениВ.
Предположим, что порт - мишень изначально
находится в некоем стандартном чистом
состоянии
.
Это состояние требуется скопировать
на порте-мишениВ.
Предположим, что порт - мишень изначально
находится в некоем стандартном чистом
состоянии
![]() .Таким
образом, начальное состояние всего
копирующего устройства есть:
.Таким
образом, начальное состояние всего
копирующего устройства есть:
![]() . (2.19)
. (2.19)
Процедура копирования подвергается некоторой унитарной эволюции U. В идеальном случае такая процедура
![]()
Предположим, что
процедура копирования работает для
каких-нибудь двух особых чистых состояний
![]() и
и![]() .
Тогда,
.
Тогда,
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
Находя скалярное (= внутреннее) произведение этих двух уравнений, получаем, что
![]()
Унитарность дает
![]() ,
а раскрывая прямое произведение векторов,
и учитывая, что
,
а раскрывая прямое произведение векторов,
и учитывая, что![]() получаем:
получаем:
![]() (2.22)
(2.22)
Но уравнение х2
= х имеет
только два решения: х
= 0 и х
= 1, поэтому
![]() =
=![]() или
или![]() и
и![]() - ортогональны. Следовательно, копирующее
устройство может копировать только
состояния ортогональные друг другу.
Отсюда, в общем случае, квантовые
состояния нельзя копировать (клонировать).
Например, квантовый клон не может
клонировать состояния кубита
- ортогональны. Следовательно, копирующее
устройство может копировать только
состояния ортогональные друг другу.
Отсюда, в общем случае, квантовые
состояния нельзя копировать (клонировать).
Например, квантовый клон не может
клонировать состояния кубита![]() = 0 и
= 0 и![]() ,т.к.
эти состояния неортогональны.
,т.к.
эти состояния неортогональны.
Т.о., квантово-механическая машина, приготавливающая копии квантовых состояний может это сделать лишь для совпадающих или ортогональных состояний. Происходит это из-за того, что, как и все квантовые операции, операция клонирования должна быть унитарной и сохранять скалярное (внутреннее) произведение. Невозможно приготовить совершенную копию неизвестного квантового состояния, используя унитарное преобразование (эволюцию). Если в копирующей машине используются неунитарные операции, то по-прежнему невозможно копировать неортогональные чистые состояния, до тех пор пока не будет удовлетворительного соответствия копируемых состояний исходным. То же относится и к смешанным состояниям.
Рассмотрим проблему копирования несколько с другой стороны. В криптографии при обмене секретными сообщениями необходимо заботиться в возможности перехвата. Тот, кто перехватывает сообщения должен уметь различить неортогональные состояния, поскольку именно их и передает Алиса.
Пусть Ева
приготавливает свой измерительный
прибор в исходном состоянии
![]() .
Ее цель - различить неортогональные
состояния
.
Ее цель - различить неортогональные
состояния![]() и
и![]() не возмущая их. Другими словами, она
хочет выполнить унитарную операцию:
не возмущая их. Другими словами, она
хочет выполнить унитарную операцию:
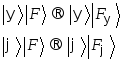
Из унитарности
операции следует, что![]() ,
т.е.
,
т.е.![]() Отсюда видно, что конечное значение
измерительного прибора будет одинаковым
в обоих случаях! Ева не возмутила (не
исказила) два неортогональных состояния,
но она и не получила никакой информации
об этих состояниях, т.к.
Отсюда видно, что конечное значение
измерительного прибора будет одинаковым
в обоих случаях! Ева не возмутила (не
исказила) два неортогональных состояния,
но она и не получила никакой информации
об этих состояниях, т.к.![]() Более
общее измерение, которое возмущает
исходные состояния, так что
Более
общее измерение, которое возмущает
исходные состояния, так что![]() и
и![]() ,
дает
,
дает

Из унитарности
следует, что
![]() Самый
лучший вариант для Евы, в смысле
оптимального различения двух состояний,
соответствует минимуму выражения
Самый
лучший вариант для Евы, в смысле
оптимального различения двух состояний,
соответствует минимуму выражения![]() .
Минимум осуществляется, когда
.
Минимум осуществляется, когда![]() ,
что как раз означает неразличимость
исходных состояний
,
что как раз означает неразличимость
исходных состояний![]() и
и![]() после операции, выполняемой Евой. Этот
пример служит наглядной иллюстрацией
связи междуинформацией,
извлекаемой при измерении и
возмущением исходных состояний.
после операции, выполняемой Евой. Этот
пример служит наглядной иллюстрацией
связи междуинформацией,
извлекаемой при измерении и
возмущением исходных состояний.
Хорошей мерой того, сколько информации получено Бобом о величине X из его измерений - это взаимная информация между X и результатом измерения Y. Боб может сделать заключение об X по результатам измерения Y только, если и только, если H(X:Y) = H(X), и что в общем случае H(X:Y) H(X). Покажем, что близость величины H(X:Y) к H(X) не самом деле дает хорошую меру того, как Боб смог определить Х. Цель Боба - выбрать измерение, которое максимизирует величину H(X:Y) и тем самым приближая ее к H(X). Для этого, определим достижимую информацию (accessible information), как максимальную величину взаимной информации. Достижимая информация - это мера того, насколько хорошо Боб смог сделать вывод о приготовленном Алисой состоянии, которая она послала ему.
Существует важное замечание, относящееся к этой дискуссии - когда концепция достижимой информации имеет классический смысл. Суть его - в различении распределений вероятностей. Представим, что Алиса готовит состояние “0” или “1” с двумя распределениями вероятностей либо с (p, 1 - p) либо с (q, 1 - q). Получая состояние Боб должен определить, какое распределение вероятности использовала Алиса для приготовления состояния. Очевидно, что Боб не всегда способен определить это с достоверностью 100%. Тем не менее, этот пример (по аналогии с достижимой информацией для квантовой системы, приготавливаемой в одном состоянии из набора смешанных состояний) очень важен. Чистые квантовые состояния обладают свойствами различимости, что является существенно отличным и богатым свойством, чем для фундаментальных объектов классической теории информации, таких как “0” и “1”.
Какова связь между
копированием и достижимой информацией?
Пусть Алиса приготавливает одно из двух
неортогональных состояний
![]() и
и![]() с соответствующими вероятностямиp
и (1 - p).
Предположим, что в этом случае достижимая
информация Боба есть Н(p),
т.е. законами квантовой механики разрешено
Бобу получить достаточно информации
при его измерении о том, какое из двух
состояний
с соответствующими вероятностямиp
и (1 - p).
Предположим, что в этом случае достижимая
информация Боба есть Н(p),
т.е. законами квантовой механики разрешено
Бобу получить достаточно информации
при его измерении о том, какое из двух
состояний
![]() или
или![]() было приготовлено Алисой. Боб может
копировать состояния очень простым
способом. Он бы выполнил измерение,
определив, какое состояние
было приготовлено Алисой. Боб может
копировать состояния очень простым
способом. Он бы выполнил измерение,
определив, какое состояние![]() или
или![]() было приготовлено Алисой и как только
он завершил идентификацию он бы приготовил
копии состояний, которые получил от
Алисы. Таким образом, теорема о запрете
копирования явилась бы следствием того
факта, что достижимая информация об
этих состояниях строго меньше, чемН(p).
Можно обратить эти рассуждения и
показать, что из теоремы о запрете
клонирования следует, что достижимая
информация меньше чем Н(p).
Представим, что возможно клонировать
неортогональные состояния. После
получения состояния
было приготовлено Алисой и как только
он завершил идентификацию он бы приготовил
копии состояний, которые получил от
Алисы. Таким образом, теорема о запрете
копирования явилась бы следствием того
факта, что достижимая информация об
этих состояниях строго меньше, чемН(p).
Можно обратить эти рассуждения и
показать, что из теоремы о запрете
клонирования следует, что достижимая
информация меньше чем Н(p).
Представим, что возможно клонировать
неортогональные состояния. После
получения состояния
![]() или
или![]() от Алисы, Боб смог бы повторно применить
клонирующее устройство для получения
состояния
от Алисы, Боб смог бы повторно применить
клонирующее устройство для получения
состояния![]() или
или![]() .
В пределе большихn
эти два состояния становятся практически
ортогональными и возможно различить
их с произвольной точностью при
проективных измерениях.
.
В пределе большихn
эти два состояния становятся практически
ортогональными и возможно различить
их с произвольной точностью при
проективных измерениях.
Таким образом,
если было бы возможным копирование, то
Боб мог бы идентифицировать с произвольно
высокой вероятностью успеха какое из
двух состояний
![]() или
или![]() было приготовлено Алисой и, таким
образом, достижимая информация была быН(p).
было приготовлено Алисой и, таким
образом, достижимая информация была быН(p).
Скрытая природа квантовой информации играет центральную роль в мощности квантовых вычислений и достижимая информация есть количественное проявление природы квантовой информации. К сожалению, не существует общего рецепта вычисления достижимой информации. В то же время имеется ряд важных достижимых границ, которые строго обоснованы. Наиболее важная из них - граница Холево. Она играет очень важную роль в теории квантовой информации.
Теорема о границе Холево
Предположим, что Алиса приготавливает состояние Х, где Х = 0,...n с вероятностями p0,...pn. Пусть Боб выполняет некое измерение этого состояния, дающее максимальное относительно всех вероятностных мер значение взаимной информации описываемое множеством элементов {Ey} = {E0,...,Em}. Результат измерения Боба есть Y. Граница Холево утверждает, что при любых измерениях Боб может достигнуть:
![]()
где
![]()
Таким образом, граница Холево является верхней границей достижимой информации.
Граница Холево играет ключевую роль при доказательстве многих положений квантовой теории информации. Рассмотрим несколько примеров.
Пример 1. В теории квантовой информации доказывается теорема (см.**), что
![]() (2.23)
(2.23)
где равенство
достигается только для тех состояний
![]() ,
которые имеют ортогональные основания
(т.е. определены на множестве ортогональных
состояний). Здесь
,
которые имеют ортогональные основания
(т.е. определены на множестве ортогональных
состояний). Здесь![]() аpx
- набор вероятностей для состояний
аpx
- набор вероятностей для состояний
![]() (
т.е.
(
т.е.![]() ).
Предположим, что неравенство в (2.23) -
строгое. Тогда, из теоремы о границе
Холево сразу следует, чтоH(X:Y)
строго меньше H(X).
Следовательно невозможно достоверно
определить X,
исходя из результатов измерений Y.
Это обобщает наше понимание того, что
если состояния, приготавливаемые Алисой
неортогональны, то Боб не может определить
с достоверностью, какое состояние было
приготовлено Алисой.
).
Предположим, что неравенство в (2.23) -
строгое. Тогда, из теоремы о границе
Холево сразу следует, чтоH(X:Y)
строго меньше H(X).
Следовательно невозможно достоверно
определить X,
исходя из результатов измерений Y.
Это обобщает наше понимание того, что
если состояния, приготавливаемые Алисой
неортогональны, то Боб не может определить
с достоверностью, какое состояние было
приготовлено Алисой.
Пример 2.
Пусть Алиса
приготавливает единичный кубит в одном
из двух квантовых состояний, в соответствии
с результатом подбрасывания монеты.
При выпадении орла Алиса готовит
состояние |0>, если же выпадает решка,
то она готовит состояние
![]() ,
где
- некоторый действительный параметр.
Цель Боба - определить какое из двух
состояний было послано.
,
где
- некоторый действительный параметр.
Цель Боба - определить какое из двух
состояний было послано.
В базисе |0>, |1> состояние можно записать следующим образом:
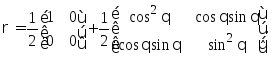
Чтобы вычислить
границу
![]() ,
найдемS().
Для этого найдем собственные значения
матрицы :
,
найдемS().
Для этого найдем собственные значения
матрицы :
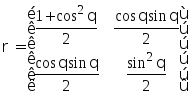
Уравнение на собственные значения:
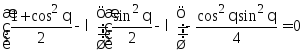
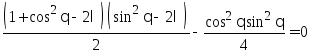
![]()

Тогда
![]() :
:
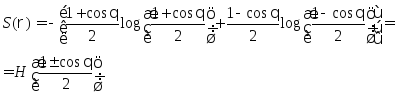
Теперь найдем
величину
![]() .
Собственные значения каждой из двух
матриц плотности равны
.
Собственные значения каждой из двух
матриц плотности равны![]() (0,
1) и
(0,
1) и![]() ,
поэтому
,
поэтому
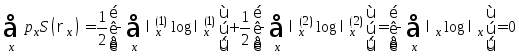
Отсюда, граница
Холево определяется бинарной энтропией
Шеннона
![]() .
Из рисунка видно, что максимум границы
достигается при
= /2
и отвечает уровню 1 бит.
.
Из рисунка видно, что максимум границы
достигается при
= /2
и отвечает уровню 1 бит.

По вертикали отложено значение границы Холево (фактически - это бинарная энтропия), по горизонтали - значение параметра в град.
Это, в свою очередь, означает, что Алиса готовит состояния, которые выбирает из ортогонального набора |0> либо |1> с равной вероятностью. Значит, Боб может достоверно определить какое из состояний было приготовлено Алисой. Для других значений граница Холево строго меньше единицы, т.е. Боб не может определить достоверно, какое из неортогональных состояний было приготовлено. С другой стороны, ясно, что при = 90 два состояния неразличимы. Поэтому при этом значении параметра Боб может угадать, какое состояние было послано с вероятностью 50%.
Границу (или
информацию Холево) можно ввести несколько
по-другому. Переобозначим величины,
входящие в это определение:
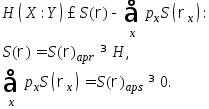
Первая величина называется априорной (безусловной) энтропией. Она описывается соответствующими диагональными элементами матрицы плотности. Апостериорная (условная) энтропия определяет вносимую каналом связи ошибку в классической схеме. В квантовой теории она отвечает за квантовую недетерминированность сигналов, связанную с соотношением неопределенности. В отсутствие классических шумов и помех апостериорная энтропия обращается в нуль. Сигналы на входе и на выходе канала при этом коррелированы и взаимная информация I() = S = H.
Достижимая информация определяется выражением Iacc = S() = H, что соответствует случаю, когда сигнал формируется из ортонормированных собственных состояний n, а операторы на выходе коммутируют с оператором плотности, т.е. когда S()aps = H()aps = 0.
В случае, когда
сигналы
![]() - это чистые состояния с нулевой энтропией,
граница Холево просто сводится к
утверждению, что
- это чистые состояния с нулевой энтропией,
граница Холево просто сводится к
утверждению, что
![]() ,
,
где
![]() - оператор плотности для ансамбля чистых
сигналов (состояний). И хотя Шенноновская
энтропияH(Х)
сообщения, посылаемого источником в
общем случае больше, чем энтропия фон
Неймана
- оператор плотности для ансамбля чистых
сигналов (состояний). И хотя Шенноновская
энтропияH(Х)
сообщения, посылаемого источником в
общем случае больше, чем энтропия фон
Неймана
![]() ансамбля сигналов, достижимая информация
(классическая) ограничена величиной
ансамбля сигналов, достижимая информация
(классическая) ограничена величиной![]() .
Таким образом ясно, что граница Холево
устанавливает связь между энтропией
фон Неймана квантового ансамбля и
(классической)
взаимной Шенноновской информацией
квантового
канала связи.
.
Таким образом ясно, что граница Холево
устанавливает связь между энтропией
фон Неймана квантового ансамбля и
(классической)
взаимной Шенноновской информацией
квантового
канала связи.
Такая связь, однако,
является довольно слабой. Дело в том,
что теорема Холево формулируется в виде
неравенства. Поэтому, в принципе, можно
сконструировать такой источник квантовых
сигналов, для которого взаимная информация
Н(X:Y)
и близко не достигает
![]() при любом выборе наблюдаемойY
при декодировании. Поэтому, хотя из
теоремы Холево и следует
информационно-теоретическое значение
величины
при любом выборе наблюдаемойY
при декодировании. Поэтому, хотя из
теоремы Холево и следует
информационно-теоретическое значение
величины
![]() ,
она не дает интерпретации
,
она не дает интерпретации![]() в терминах классической теории информации.
Например, мы не могли бы использовать
теорему Холево при интерпретации
квантовой теории некоторого макросостояния
термодинамической системы, как дающую
меру ресурсов, необходимых для
представления информации о микросостояниях
системы.
в терминах классической теории информации.
Например, мы не могли бы использовать
теорему Холево при интерпретации
квантовой теории некоторого макросостояния
термодинамической системы, как дающую
меру ресурсов, необходимых для
представления информации о микросостояниях
системы.
Ответ на этот
вопрос дает квантовая теорема кодирования
Б.Шумахера (1995). В ней классическая идея
о двоичной логике в терминах битов
заменяется моделью квантовых битов -
двухуровневых систем. Эти квантовые
биты являются фундаментальными единицами
квантовой информации. В теореме
утверждается, что энтропия
фон Неймана
![]() ансамбля является просто средним числом
кубитов, необходимых для кодирования
состояний ансамбля при помощи идеальной
кодирующей системы.
Теорему можно рассматривать как
краеугольный камень альтернативного
подхода в квантовой теории информации.
Вместо использования классической
теории информации к вероятностям,
вычисленным по законам квантовой
механики (подход Левитина и Холево), мы
пересмотрим понятия кодирования и мер
информации, которые сами по себе
определенно являются квантовыми
величинами.
ансамбля является просто средним числом
кубитов, необходимых для кодирования
состояний ансамбля при помощи идеальной
кодирующей системы.
Теорему можно рассматривать как
краеугольный камень альтернативного
подхода в квантовой теории информации.
Вместо использования классической
теории информации к вероятностям,
вычисленным по законам квантовой
механики (подход Левитина и Холево), мы
пересмотрим понятия кодирования и мер
информации, которые сами по себе
определенно являются квантовыми
величинами.
Теорема о квантовом кодировании при отсутствии шума
Пусть М
- источник квантового сигнала, который
представляется ансамблем. Этот ансамбль
описывается оператором плотности
![]() .
Пусть имеются два числа
.
Пусть имеются два числа
![]() .
.
Предположим, что имеется
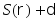 кубитов. Тогда для достаточно большого
N
(N
-это число
независимых испытаний с функцией
распределения pn)
группы из N
сигналов из источника М
могут быть переданы с помощью имеющегося
набора кубитов с качеством F
> 1 -
кубитов. Тогда для достаточно большого
N
(N
-это число
независимых испытаний с функцией
распределения pn)
группы из N
сигналов из источника М
могут быть переданы с помощью имеющегося
набора кубитов с качеством F
> 1 -
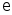 .
.Предположим, что имеется
 кубитов.
Тогда для достаточно большого N,
при передаче групп из N
сигналов от источника с помощью
имеющегося набора кубитов, качество
передачи будет F
<
кубитов.
Тогда для достаточно большого N,
при передаче групп из N
сигналов от источника с помощью
имеющегося набора кубитов, качество
передачи будет F
<
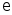 .
.
Энтропию фон
Неймана ансамбля сигналов (чистых
состояний) можно интерпретировать как
число кубитов на сигнал, необходимое
для передачи с качеством, близким к
единице. Если имеется больше, чем
![]() кубитов, при увеличении группы сигналов
можно добиться произвольно высокого
качестваF.
Если же доступно меньше, чем
кубитов, при увеличении группы сигналов
можно добиться произвольно высокого
качестваF.
Если же доступно меньше, чем
![]() кубитов, качествоF
стремиться к нулю.
кубитов, качествоF
стремиться к нулю.
Более того,
![]() является в некотором смысле количеством
кубитов, необходимым для передачи части
перепутанной системы при поддержании
качестваF
всего состояния близким к единице.
является в некотором смысле количеством
кубитов, необходимым для передачи части
перепутанной системы при поддержании
качестваF
всего состояния близким к единице.
Таким образом, энтропия S является мерой физических ресурсов, необходимых для представления информационного содержания о системе смешанных состояний. Неважно каким образом получена эта система смешанных состояний - из стохастического процесса или при выбрасывании части перепутанных состояний. Квантовая энтропия фон Неймана измеряется в кубитах.
Перенос квантовой информации. Понятие квантового канала связи.
В квантовой теории информации необходимо различать понятия копирования состояний и перенос информации из системы М в систему Х. При переносе состояние системы М передается к системе Х без сохранения копии начального состояния:
![]()
где
![]() и
и![]() - некоторые “нулевые” состояния системХ
и М.
После переноса сигнал полностью возникает
в кодирующей системе Х,
исчезая в системе М.
Одним из примеров переноса служит
явление квантовой телепортации.
- некоторые “нулевые” состояния системХ
и М.
После переноса сигнал полностью возникает
в кодирующей системе Х,
исчезая в системе М.
Одним из примеров переноса служит
явление квантовой телепортации.
Перенос является унитарной операцией для произвольных состояний из системы М. Это обеспечивает сохранение скалярного (внутреннего) произведения:
![]() для любых сигналов
(состояний)
для любых сигналов
(состояний)
![]() и
и![]() .
Это может происходить только, если
размерность гильбертова пространства
системыХ
X
не меньше
чем размерность гильбертова пространства
системы М
M.
Как происходит процесс переноса с
помощью унитарного преобразования U?
Для ответа на этот вопрос необходимо
понять как ортогональный базис из
гильбертова пространства системы М
переходит в ортогональный базис
гильбертова пространства системы Х.
После этого эволюция других состояний
будет очевидна из-за линейности.
.
Это может происходить только, если
размерность гильбертова пространства
системыХ
X
не меньше
чем размерность гильбертова пространства
системы М
M.
Как происходит процесс переноса с
помощью унитарного преобразования U?
Для ответа на этот вопрос необходимо
понять как ортогональный базис из
гильбертова пространства системы М
переходит в ортогональный базис
гильбертова пространства системы Х.
После этого эволюция других состояний
будет очевидна из-за линейности.
Перенос является обратимой операцией, поскольку состояние сигнала может быть передано назад из Х в М посредством унитарного преобразования U-1. Поэтому система связи, основанная на переносе, представляется в следующем виде. Со стороны кодирования, сигнал (квантовое состояние), исходящий из системы М, поступает в процессе унитарного преобразования U в кодирующую систему Х. Система Х переправляется от передатчика к получателю. С декодирующей стороны выполняется унитарное преобразование U-1 для возвращения сигнала из Х в М* - как идентичной копии системы М. В символьном виде:
![]()
Система Х называется квантовым каналом связи и поддерживает перенос состояний из системы М в систему М*. В общем случае для совершенной передачи (переноса) квантовый канал должен быть достаточно емким: необходимо, чтобы dimX dimM. Впрочем, иногда совершенная передача (перенос) не является необходимой; требуется лишь приближенный перенос информации из системы М в систему М*. В зависимости от характеристик сигнала можно требовать от канала связи меньшей емкости - смотря насколько качественно нам нужно его воспроизвести.
Под сигналом далее будем понимать передаваемое квантовое состояние вида:
![]() ,
,
где
![]() - оператор плотности (для чистого
состояния - это оператор проецирования),
отвечающий векторам-состояниям
- оператор плотности (для чистого
состояния - это оператор проецирования),
отвечающий векторам-состояниям![]() квантовой системыМ,
передаваемым с вероятностью p(a).
квантовой системыМ,
передаваемым с вероятностью p(a).
Для того, чтобы
определить эффективность канала нужно
ввести меру качества передачи. Пусть
начальный передаваемый сигнал системы
М
есть
![]() .
Он представляется оператором плотности
.
Он представляется оператором плотности![]() .
Конечное состояниеМ*
будет состоянием, представленным
оператором плотности wa.
В общем случае это состояние не является
чистым, поэтому wa
- необязательно оператор проецирования.
Для того, чтобы проверить насколько
близко состояние wa
находится к состоянию
.
Конечное состояниеМ*
будет состоянием, представленным
оператором плотности wa.
В общем случае это состояние не является
чистым, поэтому wa
- необязательно оператор проецирования.
Для того, чтобы проверить насколько
близко состояние wa
находится к состоянию
![]() можно произвести контрольное измерение
наблюдаемой
можно произвести контрольное измерение
наблюдаемой![]() .
Это измерение имеет два возможных
исхода: “1” - показывающее, что конечное
состояние совпадает с начальным и “0”
- показывающее, что конечное состояние
отлично от начального. Тогда вероятность
того, что конечное состояниеwa
прошло испытание есть
.
Это измерение имеет два возможных
исхода: “1” - показывающее, что конечное
состояние совпадает с начальным и “0”
- показывающее, что конечное состояние
отлично от начального. Тогда вероятность
того, что конечное состояниеwa
прошло испытание есть
![]() .
Определим точность воспроизведения
информации -качество
как общую вероятность того, что набор
сигналов (или ансамбль сигналов),
приготовленный в М
и переданный
в М*,
прошел контрольный тест, сравнивающий
его с начальным состоянием:
.
Определим точность воспроизведения
информации -качество
как общую вероятность того, что набор
сигналов (или ансамбль сигналов),
приготовленный в М
и переданный
в М*,
прошел контрольный тест, сравнивающий
его с начальным состоянием:
![]() .
.
Ясно, что качество лежит в интервале между 0 и 1. Оно равна единице только в случае, когда передача всех возможных сигналов является совершенной (идеальной). F будет близко к единице если:
сигналы с большой вероятностью р(а) искажены несильно при передаче, поэтому wa приблизительно совпадает с
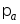 ;
;набор сигналов, который сильно возмущен, т.е. имеющий wa сильно отличную от
 имеет малую вероятность появленияр(а).
имеет малую вероятность появленияр(а).
Информация сама по себе является объективной физической величиной в ряду других — таких как масса, энергия, импульс и т. д. В квантовой теории информация — это количественная величина, характеризующая систему. В этом случае об информации говорят как об обычной физической величине, которая может принимать различные значения при изменении состояния системы. Подобно тому, как масса тела увеличивается (уменьшается) при наличии массообмена со средой, так и количество информации изменяется, если система взаимодействует с окружением — и все это объективные процессы, которые не зависят от нашего субъективного мнения. Информационные процессы — это часть физики, точно так же, как и другие процессы, приводящие к изменению той или иной физической величины. Информационным процессам отводится особая роль в силу специфических особенностей понятия «информация» в квантовой физике. Мера информации (ее количественная характеристика) вводится на основе фундаментальных принципов квантовой теории в терминах матрицы плотности. Суть квантовой информации и одновременно ее исключительная особенность — в том, что эта физическая величина как нельзя лучше подходит на роль «первичной субстанции всего сущего».
О фундаментальном значении информации пишет Б. Киви в статье «Инфо-космо-логия» (http://offline.computerra.ru/2004/544/33769/index.html): «Все больше теоретиков считают, что ключевой идеей, ведущей к „великому объединению“ гравитации и квантовой теории, может стать переформулирование взглядов на природу не в терминах материи и энергии, а в терминах информации».
Одним из первых об этом заговорил Дж. А. Уиллер: «Моя жизнь в физике представляется мне разделенной на три периода. В первый из них, растянувшийся с начала моей карьеры и до начала 1950-х годов, я был захвачен идеей, что „всё — это частицы“. Я искал способы выстроить все базовые элементы материи (нейтроны, протоны, мезоны и т. д.) из самых легких, наиболее фундаментальных частиц — электронов и фотонов. Второй период я называю „всё — это поля“. С тех пор, как я влюбился в общую теорию относительности и гравитацию в 1952 году, и вплоть до недавнего времени, я придерживался взгляда на мир, как на состоящий из полей. Мир, в котором то, что представляется нам частицами — это в действительности проявления электрических и магнитных полей, гравитационных полей и самого пространства-времени. Теперь же я захвачен новой идеей: „Всё — это информация“. Чем больше я размышляю о квантовых тайнах и о нашей странной способности постигать тот мир, в котором мы живем, тем больше вижу, вероятно, фундаментальное значение логики и информации как основы физической теории».
Возможно, в результате декогеренции появляется материя как «форма организованной информации».
Когда речь идет о квантовой теории, о количественном описании в терминах состояний, то информация — это одна из количественных характеристик системы. Можно попытаться провести аналогию со знакомыми нам мерами классической информации, которыми мы пользуемся, когда работаем на обычном компьютере. Тогда мы говорим о мегабайтах и гигабайтах информации, содержащейся в том или ином файле или на диске. Работа компьютера основана, прежде всего, на количественной теории информации, на битах, на определенном количестве ячеек памяти. Нашему компьютеру все равно, какая информация содержится в том или ином файле, когда он создается, копируется или удаляется. Для компьютера важно лишь общее количество битов, которыми мы манипулируем, и состояние каждого бита, когда файл сохраняется на диске. Способы обработки файлов и ячеек памяти, своеобразные «фундаментальные законы», согласно которым наш компьютер манипулирует информацией, не зависят от того, какие именно данные там содержатся. Например, любой файл копируется по одному и тому же «закону», независимо от того, какая в нем есть информация.
Так же и в квантовой теории — только здесь на первый план выходят не биты, а кубиты. В более широком смысле речь идет о любой системе, описываемой в терминах состояний. Такое обобщение возможно потому, что кубит — это вектор состояния произвольной двухуровневой системы, и любую более сложную систему можно рассматривать как совокупность кубитов. Обычно в квантовой теории, описывая какую-либо систему в терминах состояний, мы рассматриваем ее, как состоящую из элементарных «кирпичиков», кубитов — элементарных двухуровневых состояний.
Таким образом, любые системы в окружающей реальности можно рассматривать в терминах кубитов, как совокупность ячеек памяти квантового компьютера. (Тогда и весь Универсум, вероятно, можно представть в виде глобального и единого для всей реальности Квантового Компьютера, своеобразной всеобъемлющей Матрицы Плотности). Поэтому Р. Фейнман и говорил об исключительно важной роли квантовых компьютеров в постижении законов природы. Понимание фундаментальных принципов работы квантового компьютера, в отличие от обычного, уже не ограничивается конкретными техническими устройствами. (Это и будет означать более глубокое понимание фундаментальных законов окружающей реальности, согласно которым «функционирует» весь наш Универсум). Процессы декогеренции/рекогеренции, то есть перехода нелокального (чисто информационного) состояния в локальное и обратно, манипулирование квантовой запутанностью кубитов и т. д. — все это физические процессы, которые происходят в окружающей нас реальности, причем на самом фундаментальном ее уровне.
Имея дело с классической информацией, мы разделяем саму информацию и физический носитель. В результате чего можем лишь приспособить какой-либо материальный объект для хранения (передачи) определенного количества «классической» информации. Получается, что без материального носителя информация не может существовать. Поэтому и возникают иногда вопросы, где содержится квантовая информация, и что является ее носителем? В квантовой теории информация - это физическая величина, характеризующая систему, т. е. сама система и является носителем квантовой информации.
Квантовое описание на сегодняшний день — это самое полное теоретическое описание из всех известных. И в случае чистого состояния, когда мы описываем замкнутую систему, то на вопрос, где содержится информация об этой системе, следует очевидный ответ: информация содержится в самой системе, это одна из ее количественных характеристик.
Основывается эта мера на понятии частичной матрицы плотности и выражается в терминах энтропии фон Неймана:
S(ρA) = – Sp[ρA log2(ρA)].
Здесь ρA — частичная (редуцированная) матрица плотности подсистемы А. Получается она взятием частичного следа по B. С физической точки зрения, взятие частичного следа и получение редуцированной матрицы плотности — это усреднение по всем внешним степеням свободы выделенной подсистемы (по ее внешнему окружению). В некотором отношении это проведение границы между подсистемой и ее окружением, когда подсистема может рассматриваться независимо от него. Мы как бы «вырезаем» нашу подсистему из более сложной структуры и рассматриваем ее в качестве самостоятельного объекта. В результате этой операции пространство допустимых состояний подсистемы уменьшается, частичная матрица плотности имеет меньшую размерность, чем исходная система, например, из матрицы 4 × 4 получается матрица 2 × 2.
Мера информации в квантовой теории определяется на основе понятия матрицы плотности. Мера информации вводится так: количество информации I в системе численно равна следу квадрата матрицы плотности, то есть
I = Sp(ρ2). (2.24)
Это определение легко объясняется с физической точки зрения. Согласно обычным правилам квантовой механики, любой физической величине, которую мы хотим использовать в качестве количественной характеристики системы, ставится в соответствие линейный самосопряженный оператор Q. И численное значение этой физической величины получается из выражения:
<Q> = Sp(ρ Q). (2.25)
Сравнивая с предыдущим выражением, мы видим, что меру информации можно рассматривать как количественную характеристику системы, когда физической величиной является сама система, точнее, матрица плотности, выступающая в данном случае в качестве оператора физической величины, то есть
I = <ρ> = Sp(ρ ρ).
Из этого следует, что квантовая информация является самой фундаментальной количественной характеристикой системы, поскольку для ее определения нет необходимости вводить дополнительные соображения о том, какие еще физические величины (операторы) характерны для данной системы. Квантовая информация, как мера, существует всегда, если есть система, независимо от того, в каком состоянии она находится. Информация сама по себе является физической сущностью и существует даже тогда, когда система находится в нелокальном состоянии, поэтому ее можно считать «первичной субстанцией», из которой в процессе декогеренции могут «проявляться» локальные объекты. «Информация физична» в прямом смысле — она является источником всех других физических процессов и материальных проявлений, которые могут иметь место в системе.
Отсюда и более высокий статус квантовой информации относительно других физических величин, которые мы могли бы дополнительно привлечь для описания системы. А поэтому выше и значимость закона сохранения квантовой информации по сравнению с другими законами сохранения
Мы рассмотрели, каким образом вводится мера информации, исходя из основополагающих принципов квантовой теории. При таком определении для любого чистого состояния (замкнутой системы) мера информации равна 1 (следствие нормировки амплитуд вектора состояния). Это максимальное значение — то есть для любой изолированной системы информация максимальна и равна единице. Для смешанных состояний (открытых систем) информация меньше единицы, и минимальное ее значение достигается для максимально смешанных состояний и равно 1/d, где d = 2N — размерность гильбертова пространства (N — число двухуровневых подсистем). Таким образом, количество информации, содержащейся в системе, изменяется от 1/2N для максимально смешанных состояний до 1 для чистых состояний (изолированных систем). С физической точки зрения это легко объяснить. В замкнутой системе вся информация содержится в ней самой, и нормированная ее величина равна 1. Для смешанных состояний, то есть для систем, взаимодействующих со своим окружением, часть информации о системе теряется в ее окружении. И минимум информации, который может остаться в самой системе (случай максимально смешанного состояния), определяется числом локализованных структур в системе в процессе декогеренции (при этом взаимодействие с окружением сопровождается декогеренцией, то есть локализацией системы и ее составных частей из изначально нелокального информационного состояния).
Однако определение (2.24) не совсем удобно в практическом плане. Для нас привычнее иметь дело с аддитивными величинами, когда информация составной системы равняется сумме частичных информаций. А согласно определению (2.24), информация не суммируется, а перемножается. Так, для двусоставной системы (в случае некоррелированного, то есть сепарабельного состояния)
IAB = Sp(ρАВ)2 = Sp(ρА)2 Sp(ρВ)2 = IA IB.
Поэтому удобнее перейти к логарифму от этой величины. Поскольку логарифм произведения равен сумме логарифмов сомножителей, получается аддитивность. При этом ln[Sp(ρ2)] изменяется в пределах от –lnd до 0.
Из статистической механики известно, что на больших временах энтропия системы соответствует среднему значению –k lnρ, где k — постоянная Больцмана, так что согласно (2.25) имеем:
<–k lnρ > = –k Sp(ρ lnρ)
Отсюда связь между количеством информации в системе и энтропией
Sp(ρ lnρ) = <lnρ>,
которая называется энтропией фон Неймана и чаще всего используется сейчас в качестве меры квантовой информации. Она и была введена в качестве первой меры квантовой запутанности. Различие между натуральным логарифмом и логарифмом по основанию 2 в данном случае не принципиально.
Заметим, что Sp(ρ lnρ) и ln[Sp(ρ2)] изменяются в одних и тех же пределах и никогда сильно не отличаются друг от друга. Однако при использовании этой меры, чтобы получить положительное число, приходится в выражениях ставить знак минус. При этом иногда забывается, что при переходе к логарифму с информацией произошел своеобразный «перевертыш»: там, где был минимум информации, — теперь стал максимум, а максимум информации (единица для чистого состояния) обратился в нуль. Хотя и эту ситуацию можно трактовать так, что, с точки зрения внешнего наблюдателя, о чистом состоянии он ничего не может сказать, поскольку это замкнутая система, которую наблюдатель еще не «потревожил» своим измерением.
Квантовая теория информации, таким образом, непосредственно связывает информацию с энергией через энтропию фон Неймана, которую можно считать основной физической характеристикой энергоинформационного процесса. Изменение информации сопровождается изменением энергии, а обмен информацией напрямую связан с обменом энергией (справедливо и обратное) — это еще один важный вывод, который сделан в физике квантовой информации.
Есть и отдельные строгие результаты, связывающие информацию, энергию и энтропию. В частности, теорема Марголюса-Левитина утверждает, что число элементарных логических операций, которые физическая система может выполнить в единицу времени, ограничено энергией системы, а количество информации, которую система может зарегистрировать (воспринять), ограничено ее собственной максимальной энтропией.
Прямая связь между энергией и выполняемыми логическими операциями (информационными процессами) позволяет перекинуть мостик к физическим процессам, сопровождающим работу сознания, поскольку она непосредственно связана с логическими операциями.
Информация в терминах энтропии фон Неймана позволяет описывать запутанные состояния. Одна из основных особенностей этого понятия состоит в том, что об объекте, находящемся в чистом запутанном состоянии (ρ = ρ2), невозможно получить никакой информации, поскольку в этом случае S(ρ) = 0. Энтропия фон Неймана и квантовая запутанность может быть отлична от нуля только для подсистем, которые взаимодействуют со своим окружением, и поэтому находятся в несепарабельном состоянии.
Довольно часто для простоты количество квантовой информации определяется просто как число кубитов в системе.
Исходная величина Sp(ρ2) сейчас тоже широко используется в физике квантовой информации, но уже не в качестве меры информации, а как характеристика степени чистоты состояния, которая показывает, насколько близко данное состояние к чистому, для последнего Sp(ρ2) = 1.