
Дзержинский. Дискретная математика
.pdf
Легко проверить, что они монотонны. Теорема 1.
(x1,…,xn) является монотонной тогда и только тогда, когда ее сокращенная ДНФ не содержит отрицаний.
Теорема 2.
Множество всех монотонных функций является замкнутым классом и обозначает M.
[M] = M
Доказательство
Проведем это доказательство для частного вида суперпозиция, отсюда ясно как сделать его для общего случая.
Пусть
(x1,…,xn), (x1,…,xn), (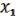 ,
, 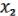 ) M. (21.4)
) M. (21.4)
Рассмотрим
F(x1,…,xn) = ( (x1,…,xn), (x1,…,xn)). (21.5)
Требуется доказать что F M, тем самым будет доказано, что класс M замкнут.
Пусть ,  , причем (т.е. i i ). Следует доказать F( ) F( ). Из того, что ,
, причем (т.е. i i ). Следует доказать F( ) F( ). Из того, что , 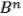 ,
,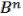 M что ( ) ( ); F ( ) F ( ).
M что ( ) ( ); F ( ) F ( ).
2.23 Самодвойственные функции.
Двойственность, напомним, вводилась следующим образом:(x1,…,xn), – булева функция.
(x1,…,xn) = (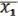 , …,
, …, 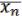 ). (28.1)
). (28.1)
Определение: булева функция (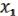 , …,
, …, 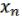 ) называется самодвойственной, если
) называется самодвойственной, если
f= ( 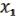 , …,
, …, 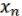 ), т.е. другими словами:
), т.е. другими словами:
= f (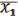 , …,
, …, 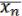 ) (28.2)
) (28.2)
или
f (x1,…,xn) = (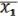 , …,
, …, 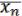 ). (28.3)
). (28.3)
Теорема.
Класс всех самодвойственных функций S является замкнутым.
[S] = S.
Доказательство.
Вытекает из принципа двойственности.
Пусть (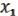 , …,
, …,  ), (
), (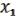 , …,
, …, 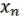 ), … (
), … (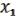 , …,
, …,  ) S (28.4)
) S (28.4)
43
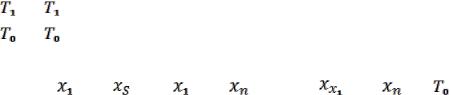
Рассмотрим их суперпозицию
F(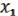 , …,
, …, 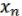 ) = ( (
) = ( (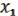 , …,
, …, 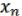 ), …, (
), …, (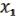 , …,
, …, 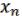 )). (28.5)
)). (28.5)
Нужно доказать:  = F. Принцип двойственности:
= F. Принцип двойственности:
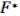 (
(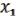 , …,
, …,  ) = (
) = (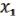 , …,
, …, 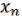 ), … (
), … ( , …,
, …, 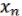 )
)
В силу самодвойственности
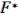 = (
= ( , …,
, …, 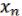 ) = F(
) = F(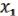 , …,
, …, 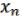 ) (28.6)
) (28.6)
ч.т.д.
2.24 Классы функций, сохраняющих константу.
Определение: классом функций, сохраняющим 0, называются все булевы функции (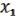 , …,
, …, 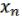 ), для которых выполнено: (0, …,0) = 0. Обозначение:
), для которых выполнено: (0, …,0) = 0. Обозначение: 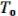 .
.
Классом функций, сохраняющих 1, называются все булевы функции (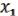 , …,
, …, 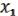 ), для которых выполняется (1, …, 1) = 1. Обозначение:
), для которых выполняется (1, …, 1) = 1. Обозначение: 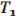 .
.
Эти оба класса оказываются замкнутыми.
Теорема.
Классы функций, сохраняющих const, являются замкнутыми
[ ] = ; |
|
[ ] = . |
|
Доказательство. |
|
Пусть ( , …, ), 2 ( , …, ), …, s ( |
, …, ) (29.1) |
Рассмотрим их суперпозицию. |
|
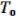 F(
F(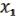 , …,
, …, 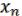 ) = ( 2(
) = ( 2(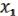 , …,
, …, 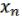 ), …, s (
), …, s (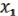 , …,
, …,  )). (29.2)
)). (29.2)
Проверим это, вычислив:
F(0, …, 0) = ( 2 (0, …, 0), …, s (0, …, 0)) = (0, …, 0) = 0 (29.3)
Таким образом [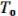 ] =
] =  .
.
Вторая часть теоремы доказывается аналогично. Подведем итоги.
Замкнутыми являются классы L, M, S, 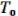 ,
,  . Эти классы называются основными замкнутыми классами функций.
. Эти классы называются основными замкнутыми классами функций.
2.25 Теорема о функциональной полноте (Поста).
Это одна из основных теорем курса. Позволяет определить любой системе функций, является ли она полной.
Теорема.
44
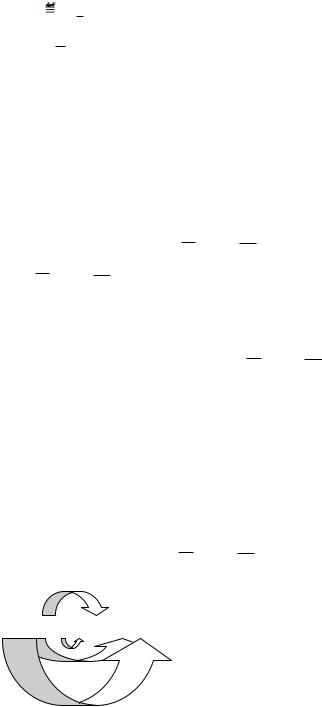
Система булевых функций = {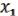 , …,
, …,  }, является функционально полной тогда и только тогда, когда она не содержится целиком ни в одном из основных замкнутых классах функций.
}, является функционально полной тогда и только тогда, когда она не содержится целиком ни в одном из основных замкнутых классах функций.
Другими словами: для каждого из основных классов найдется в сумме хоть бы одна функция, которая в нем не лежит (может быть одна и та же).
Лемма 1 (о несамодвойственной функции).
Если булева функция 1 ( , …,
, …, 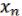 ) несамодвойственна ( S), то, подставляя в нее вместо
) несамодвойственна ( S), то, подставляя в нее вместо 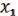 , …,
, …, 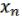 переменную x или
переменную x или 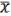 , можно получить булеву функцию (x), тождественно равную const (0; 1).
, можно получить булеву функцию (x), тождественно равную const (0; 1).
(x) = 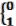 (24.1)
(24.1)
Доказательство.
x, 1
(24.2)
x, 0
0 = ,
 1 =
1 =
(чтобы проверить, нужно рассмотреть 0 = 0; 1 = = 1). Рассмотрим (x) = ( 1 1 , 2 2 , …, n n ).
Поскольку ( , …,
, …, 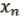 ) несамодвойственная, найдется хотя бы один
) несамодвойственная, найдется хотя бы один
набор 1, …, n 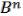 , такой что f* ( 1, …, n) ( 1, …, n), иначе бы эта функция была бы самодвойственной.
, такой что f* ( 1, …, n) ( 1, …, n), иначе бы эта функция была бы самодвойственной.
Другими словами ( 1 , …, n ) ( 1, …, n) т.е. всего два значения:
( 1 , …, n ) = ( 1, …, n),
хотя бы на одном наборе. Покажем, что (0) = (1).
(0) = ( 0 1 , 0 2 , …, 0 2 ) = ( 1 , …, n )
Заметим, что
(1 1 , 1 2 , …, 1 2 )= (1).
Начали с (0), а закончим в (1) (0) = (1), т.о. – const.
Пример.
(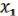 ,
,  ,
,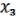 ) = (10110110)
) = (10110110)
Проверим, что S (не является самодвойственной).
Если =( 1, …, n), то =( 1 , …, n )
( 1 0 1 1 0 1 1 0) – не самодвойственная.
45

(000) = 1 cамодв. (111) = 0_______(инверсия)(001) = 0 самодв. (110) = 1(010) = 1 несамодв. (101) = 1
Достаточно найти 1 несамодвойственный набор, и функция будет несамодвойственна.
( , , )
(1)= (0,1,0) = 1(0)= (1,0,1) = 1
(0)= (1)=1 (0)= (1), ч.т.д.
Лемма 2 (о немонотонной функции).
Если функция M  (
(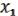 , …
, …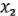 ) – немонотонная, то, подставив в нее вместо одного из переменных x, а вместо остальных некоторые const (0, 1), можно получить функцию (x) =
) – немонотонная, то, подставив в нее вместо одного из переменных x, а вместо остальных некоторые const (0, 1), можно получить функцию (x) = 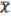 .
.
Доказательство.
Носит конструктивный характер, показывая, как решать задачи. Т.к. M найдутся два набора = ( 1, …, n); = ( 1, … n ) такие, что ; ( )
( ).
Соединим две вершины , 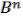 куба некоторым путем, проходящим по ребрам , т.е.
куба некоторым путем, проходящим по ребрам , т.е. 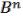 , что 1 2 … k< , и .
, что 1 2 … k< , и .
Пример.
Рис.21.
Поскольку i, i+1 являются соседними вершинами в кубе 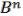 , они отличаются лишь одной координатой.
, они отличаются лишь одной координатой.
Имеется ( ) = 1, ( ) = 0.
46

Пусть вариация значения функции происходит на паре соседних вершин i ;
т.е. ( i) = 1, ( i+1) = 0. Раз эти вершины соседние, то они отличаются одной координатой (пусть, например, в 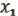 ) .
) .
имеет такой вид:
i = (0, 1, 2, …, N-1) = i+1 (1, 1, 2, …, N-1)
(x) = (x,х1 ,х2 , …, хn).
Проверим, что (x) = 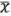 :
:
(0) = (0, 1, 2, …, N-1) = ( i) = 1 = x ;
(1) = (1, 1, 2, …, N-1) = ( i+1) = 0 = x
Ч.т.д.
Лемма 3 о нелинейной функции.
Если булева функция (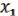 , …,
, …, 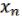 ) L нелинейна, то с помощью подстановки вместо переменных
) L нелинейна, то с помощью подстановки вместо переменных 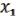 , …,
, …, 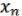 величин x,
величин x, 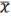 или 0, 1 constant, взятие отрицания от самой функции можно получить конъюнкцию
или 0, 1 constant, взятие отрицания от самой функции можно получить конъюнкцию 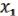 &
& 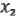 .
.
Доказательство.
Одновременно конструктивно показывается, как это сделать. Представим функцию (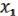 , …,
, …, 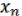 ) в виде МЖ. Поскольку нелинейна, то найдется в МЖ одночлен, слагаемое, содержащее произведение каких-либо переменных. Пусть, например,
) в виде МЖ. Поскольку нелинейна, то найдется в МЖ одночлен, слагаемое, содержащее произведение каких-либо переменных. Пусть, например, 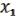 &
& 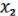 . Сгруппируем все слагаемые, содержащие
. Сгруппируем все слагаемые, содержащие 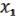 &
&  , и вынесем их за скобки. Затем сгруппируем остальные слагаемые, содержащие
, и вынесем их за скобки. Затем сгруппируем остальные слагаемые, содержащие 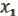 , и вынесем
, и вынесем 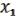 за скобки. Затем сгруппируем остальные слагаемые, содержащие
за скобки. Затем сгруппируем остальные слагаемые, содержащие 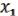 , и вынесем
, и вынесем  за скобки. Среди остальных сгруппируем слагаемые
за скобки. Среди остальных сгруппируем слагаемые 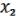 и вынесем за скобки. Получим:
и вынесем за скобки. Получим:
(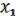 , …,
, …, 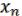 ) =
) = 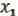
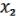 0 (
0 ( , …,
, …, 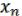 )
) 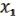 1 (
1 (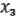 , …,
, …, 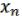 )
)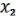 2 (
2 (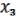 , …,
, …, 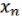 ) 3 (
) 3 (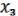 , …,
, …,  ).
).
 не зависит, ни от
не зависит, ни от  , ни от
, ни от 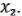
Придадим  , …,
, …, 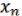 такие значения 3, …, n , чтобы 0 ( 3, …, n ) 0.
такие значения 3, …, n , чтобы 0 ( 3, …, n ) 0.
Обозначим значение 1( 3, …, n) = a; 2( 3, …, n) = b; 3( 3, …, n) = c. Какие это числа (a, b, c) зависит от функции.
Тогда можно записать, что булева функция:
(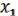 ,
, 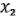 , 3, …, n) =
, 3, …, n) = 
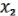 1 a
1 a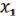 b
b с
с
Важное свойство двоичной суммы:
x d= 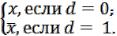
Рассмотрим функцию без индекса:
(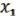 ,
, 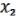 ) = (
) = (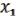 b,
b,  a, ( 3, …, n ) ab с Если ab с 0, то (
a, ( 3, …, n ) ab с Если ab с 0, то (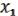 ,
, 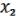 ) = (
) = (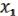 ,
, 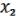 ,( 3, …, n)).
,( 3, …, n)).
47
Проверим, что:
( ,
, 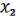 ) =
) =  &
& 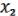 = (
= (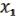 b) & (
b) & (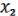 a)
a)
a(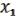 b) b(
b) b(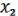 a) c
a) c
ab c.
Раскроем теперь все скобки (будем иметь в виду, что d d = 0, т.е. можно приводить подобные):
(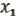 ,
, 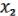 ) =
) = 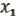
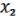 a
a 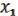 b
b 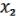 ab
ab
a 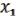 ab b
ab b 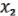 ab c ab
ab c ab
c = 
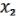
ч.т.д.
Пример (на использование леммы).
= (1111 0001) – булева функция трех переменных (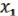 ,
,  ,
, 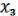 ). Проверим, что
). Проверим, что
L. Найдем МЖ для нее в самом общем виде:
(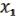 ,
, 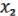 ,
, 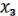 ) =
) = 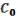


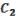
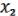
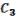

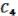
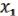
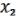

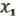
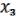
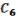
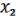

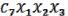 .
.
Коэффициенты 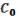 ,
, 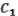 , …,
, …, 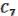 находятся из условия.
находятся из условия.
(000) = 1 |
= ; |
(001) = 1 |
= 1 = 0; |
(010) = 1 |
= 1 |
Всего будет восемь равенств и находим восемь неизвестных коэффициентов. Ответ будет таким:
( , , ) = |
1 L (т.к. член |
). |
Согласно лемме можно получить конъюнкцию: |
|
|
( ) = ; = 1= 3 |
|
|
( ) = 1 |
|
|
( ) = 0 |
|
|
( ) = 1. |
|
|
Тогда: |
|
|
( , , 1) = |
1; |
|
Значит a = 1; b = 0; c = 1.
(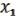 ,
, 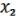 ) = (
) = (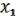 ,
,  1, 1) 1 = (
1, 1) 1 = (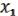 ,
, 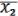 , 1) =
, 1) = 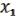 &
& 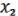 .
.
Следствие из рассмотрение результата данного примера нам важно:
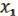
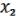 = (
= (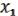 ,
, 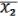 , 1).
, 1).
48

2.26 Доказательство теоремы о функциональной полноте.
Мы рассматриваем вопрос, когда система = {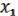 , …,
, …,  } полна, т.е. через формулы можно вывести любую булеву функцию. Мы ввели пять основных классов
} полна, т.е. через формулы можно вывести любую булеву функцию. Мы ввели пять основных классов 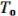 ,
, 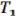 , L, M, S. Теорема утверждает, что если не содержится целиком в каком-либо из классов, то она полна. Это необходимые и достаточные условия.
, L, M, S. Теорема утверждает, что если не содержится целиком в каком-либо из классов, то она полна. Это необходимые и достаточные условия.
1.Необходимость.
Пусть система полна. Докажем, что она не содержится целиком в одном из замкнутых классов. Вспомним определение замкнутого класса. Если бы система принадлежала 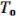 , то из функций
, то из функций 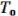 , путем суперпозиций над получались бы функции только из
, путем суперпозиций над получались бы функции только из 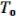 (по определению замкнутого класса) система не была бы полна. Для любого другого класса аналогично.
(по определению замкнутого класса) система не была бы полна. Для любого другого класса аналогично.
2. |
Достаточность. |
|
Обозначим функцию из системы , которая не лежит в : f0; |
f1; L |
|
f2; M |
f3; S f4. (Т.е. производим перенумерацию функций). |
При этом |
некоторые из f0, f1, f2, f3, f4 могут совпадать.
1) Покажем, что из функций можно получить Const 0, 1 (с помощью суперпозиции). Поскольку f0 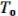 f0(0, 0, …, 0) 0 f0 = 1. Возможно а) f0
f0(0, 0, …, 0) 0 f0 = 1. Возможно а) f0
(1, …, 1) = 1; б) f0 (1, …, 1) = 0.
Рассмотрим для а): (x) = f0 (x, x, …, x). Тогда
(0) = f0 (0, …,0) = 1; (1) = f0 (1, …,1) = 1. Итак
(x) = f0 (x, …, x) 1 («Тождественная единица»).
Поскольку f0 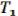 f0 (1, 1) = 0. Т.к. const «1», мы уже получили, то теперь получим «0».
f0 (1, 1) = 0. Т.к. const «1», мы уже получили, то теперь получим «0».
0 = f1 (f0(x, …, x), f0(x, …, x), …, f0(x, …, x)).
Рассмотрим теперь б): (x) = f0(x, …, x). Тогда получаем (0) = f0(0, …, 0) = 1;
(1) = f0 (1, …, 1) = 0 (x) = 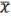 .
.
Теперь применим лемму 1 о несамодвойственной функции. Можно, согласно нее, взять f4 S, и подставить в нее вместо 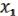 , …,
, …,  x и
x и  , и получить Const. Какую Const – не ясно, «0» или «1».
, и получить Const. Какую Const – не ясно, «0» или «1».
Если при этом получится 0, то Const 1 получаем так:
1 = (0) = f0 (0, …,0).
Если же по лемме 1 получится constant 1, то
0 = (1) = f0 (1, …, 1).
49
Теорема 1 доказана. Мы получили во всех случаях Const 0 или 1.
2)Покажем, что с помощью функции из можно получить  . Согласно лемме 2 о немонотонной функции, взяв f3 M, можно, подставив вместо n – 1 переменных constant 0, 1 (которые уже получены выше), получить
. Согласно лемме 2 о немонотонной функции, взяв f3 M, можно, подставив вместо n – 1 переменных constant 0, 1 (которые уже получены выше), получить 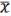 .
.
3)Покажем, что с помощью булевой функции из можно получить конъюнкцию из 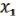 &
& 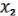 . Согласно лемме 3 о немонотонной функции, взяв f2 L, можно, подставив в нее вместо переменных
. Согласно лемме 3 о немонотонной функции, взяв f2 L, можно, подставив в нее вместо переменных 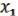 ,…,xn; constant 0, 1 и, взяв, если нужно, отрицание , получить конъюнкцию
,…,xn; constant 0, 1 и, взяв, если нужно, отрицание , получить конъюнкцию 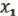 &
& 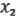 .
.
4)Полнота системы теперь из теоремы 1, если в качестве системы сравнения  взять систему 1 = {&, ͞ }– полна. Каждый из системы
взять систему 1 = {&, ͞ }– полна. Каждый из системы  по доказательству выше (и & ͞ ) выражается через систему .
по доказательству выше (и & ͞ ) выражается через систему .
Значит и полна.
Теорема о полноте доказана.
Пример.
Проверить полноту = {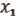 , …,
, …,  }, где f1 = {1111 0001}, f2 = {1111 0000}, и
}, где f1 = {1111 0001}, f2 = {1111 0000}, и
выразить через & и ͞ следующие функции: 0, 1, , & |
и |
. |
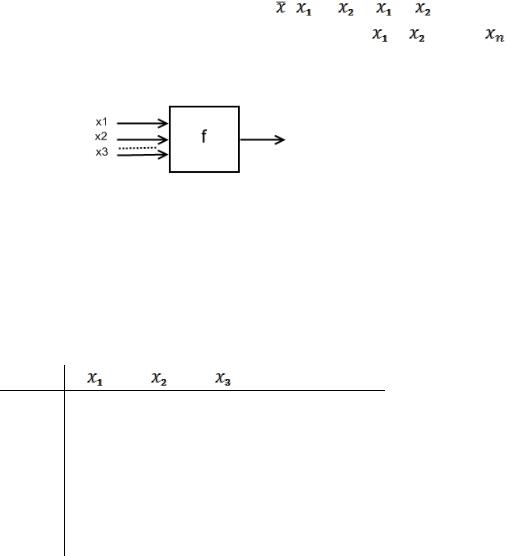
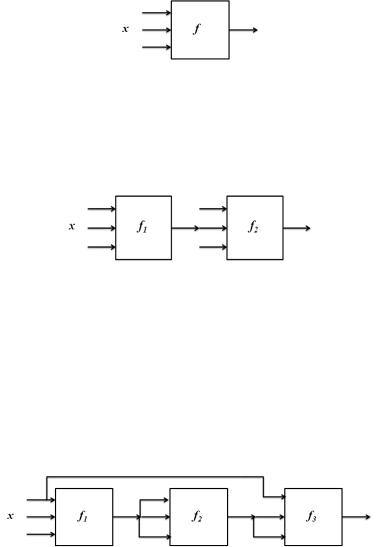
Функциональным элементом (ФЭ) булевой функции |
f ( |
, , …, ) |
называется устройство с n входами и одним выходом. Обозначение:
Рис.22.
Если на входе этого устройства подаются значения переменных 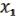 , …,
, …,  соответственно, то на выходе этого устройства возникает сигнал (
соответственно, то на выходе этого устройства возникает сигнал (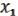 , …,
, …, 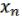 ). Как оно устроено – пока не важно.
). Как оно устроено – пока не важно.
Итак, составим таблицы функций 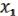 ,
, 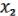 .
.
Пример.
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
50
1.Проверим полноту. Для  f0.
f0.
2.Для 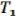 f1.
f1.
3.Для L. Воспользуемся предыдущим примером. По его результатам
L f2.
4.Для M. ( ; ( ) ( ))
Возьмем = (000), = (100); но f ( ) f ( ). Функция  тоже немонотонная.
тоже немонотонная.
5.Остался класс S. f S (т.к. если взять значение (000)  (000)).
(000)).
6.Выразим через классы const 0, 1.
Для этого берем f( ,
,  ,
, 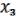 ), т.к. она
), т.к. она 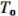 .
.
f (0, 0, 0) = 1; f(0, 0, 0) = 1, т.е. это случай а) нашего доказательства (x) = f(xxx) 1.
Реализация
Рис.23.
Далее:
f (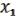 ,
, 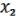 ,
, 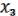 )
) 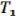 ; f (1, 1, 1) = 0.
; f (1, 1, 1) = 0.
Реализация рис.24.
Рис.24.
Будем искать отрицание: 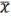 .
.
По второму пункту, доказательства 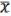 нужно искать с помощью немонотонной функции. Согласно лемме о немонотонной функции, для
нужно искать с помощью немонотонной функции. Согласно лемме о немонотонной функции, для  (
(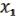 ,
,
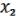 ,
, 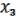 ) M. ; f ( ) f ( ). После чего мы cоединяем вершины. Для и делать этого уже не надо – они рядом.
) M. ; f ( ) f ( ). После чего мы cоединяем вершины. Для и делать этого уже не надо – они рядом.
(x) = f (x, 0, 0) =  . Схема решения рис.25.
. Схема решения рис.25.
Рис.25.
51

Пример. |
|
|
= { , …, } – полноту проверили. |
|
|
f1 |
= (1101 0001) |
|
f2 |
= (1111 0001) |
|
Надо было б) выразить булеву функцию через , а именно 0, 1, |
͞ , &, |
|
Часть была сделана, немного громоздко, но: |
|
|
1 |
= f (x, x, x) (25.17) |
|
0 |
= f (1, 1, 1) = f (f (x, x, x); f (x, x, x); f (x, x, x)) |
|
|
= f (x, 0, 0) = f (x, f (1, 1, 1), f (1, 1, 1) ). |
|
Соответствующие функциональные схемы приведены выше.
Можно построить функциональную схему для любой булевой функции.
Через функциональные элементы можно выразить любое арифметическое действие, интеграл, дифференциал и т.д.
С помощью леммы о нелинейной функции для
f1 (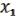 ,
, 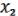 ,
, 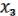 )
) 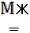

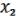
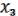
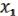 1.
1.
С помощью можно получить &:
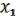 &
& 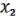 = f1 (
= f1 ( ,
, 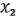 , 1) (См. выше)
, 1) (См. выше)
Можно пользоваться ͞ для &.
Однако, посмотрев внимательно на f1, f2, схемы можно нарисовать проще, чем по алгоритму (менее громоздко).
Легко понять, что f легко задать аналитически. f1 = 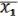
Замечание к ФЭ ͞ . Можно получить проще, если заметить, что f1 (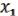 ,
, 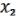 ,
, 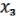 ) =
) = 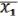 ,
,
Т.е. что  ,
,  - несущественные переменные.
- несущественные переменные.
Рис.26. Схема для конъюнкции
52
