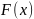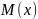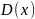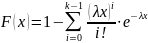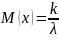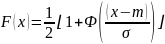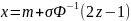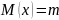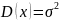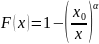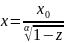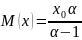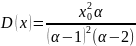9373_ЗаболотниковМЕ_ЛР_3
.docxМинистерство науки и высшего образования РФ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Информационных систем
отчёт
по лабораторной работе №3
по дисциплине «Моделирование систем массового обслуживания»
Тема: Моделирование непрерывной случайной величины
Студент гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Татарникова Т.М. |
Санкт-Петербург
2022
Цель работы.
Выполнить программную реализацию генератора непрерывной случайной величины со заданным законом распределения.
Ход работы.
Сперва рассмотрим экспоненциальное распределение. Оно описывается следующей формулой:
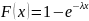
и имеет математическое ожидание и дисперсию, рассчитываемые, соответственно, как:
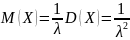
Для построения
генератора такой случайной величины
будем использовать метод обращения, то
есть решим уравнение
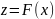 .
Получаем решение:
.
Получаем решение:

Для работы будем
использовать выборку из
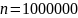 значений. Параметр
значений. Параметр
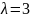 .
Соответственно, теоретические значения
первого и второго момента равны:
.
Соответственно, теоретические значения
первого и второго момента равны:
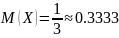
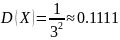
Эмпирические значения нам даст программа. Получаем следующие результаты (см. рис. 1):
![]()
![]()
Рисунок 1 – Первый и второй моменты, вычисленные эмпирическим путём
Как видим, результаты схожи с точностью до тысячных для математического ожидания и с точностью до сотых для дисперсии.
Гистограмма распределения выглядит следующим образом (см. рис. 2):
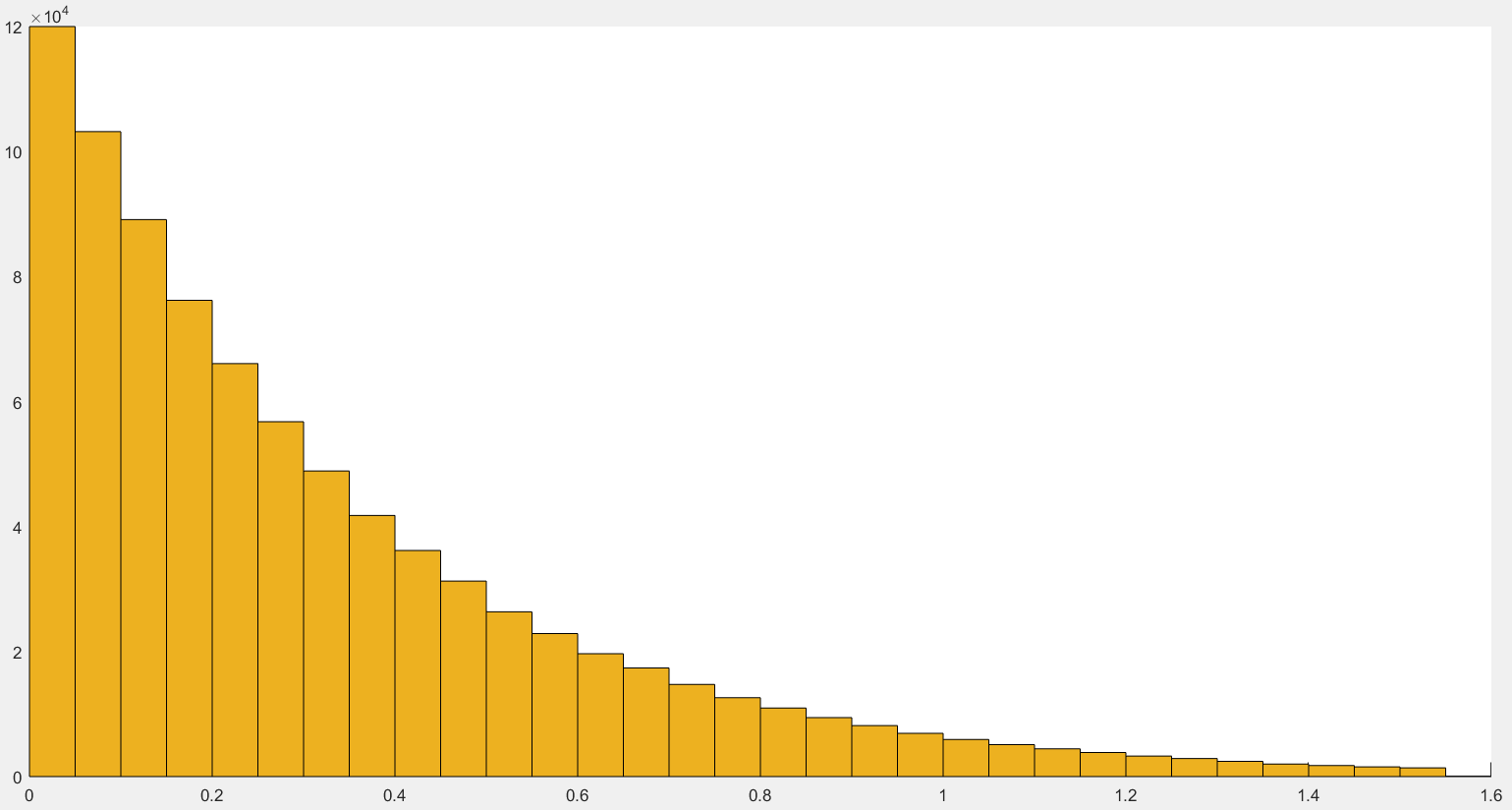
Рисунок 2 – Экспоненциальное распределение
Далее рассмотрим равномерное распределение. Данное распределение описывается формулой:
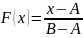
и имеет математическое ожидание и дисперсию, которые рассчитываются по формулам:
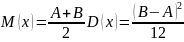
Методом обращения
получаем модель случайной величины
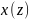 :
:
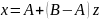
Параметры
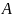 и
и
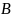 возьмём равными соответственно 0 и 3.2.
В таком случае теоретические значения
первого и второго момента равны:
возьмём равными соответственно 0 и 3.2.
В таком случае теоретические значения
первого и второго момента равны:
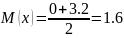
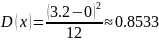
По результатам работы программы получаем эмпирические оценки математического ожидания и дисперсии (рис. 3):
![]()
![]()
Рисунок 3 – Первый и второй моменты, вычисленные эмпирическим путём
Точность вычислений также показывается достаточно хорошая. Теперь построим гистограмму равномерного распределения (рис. 4):
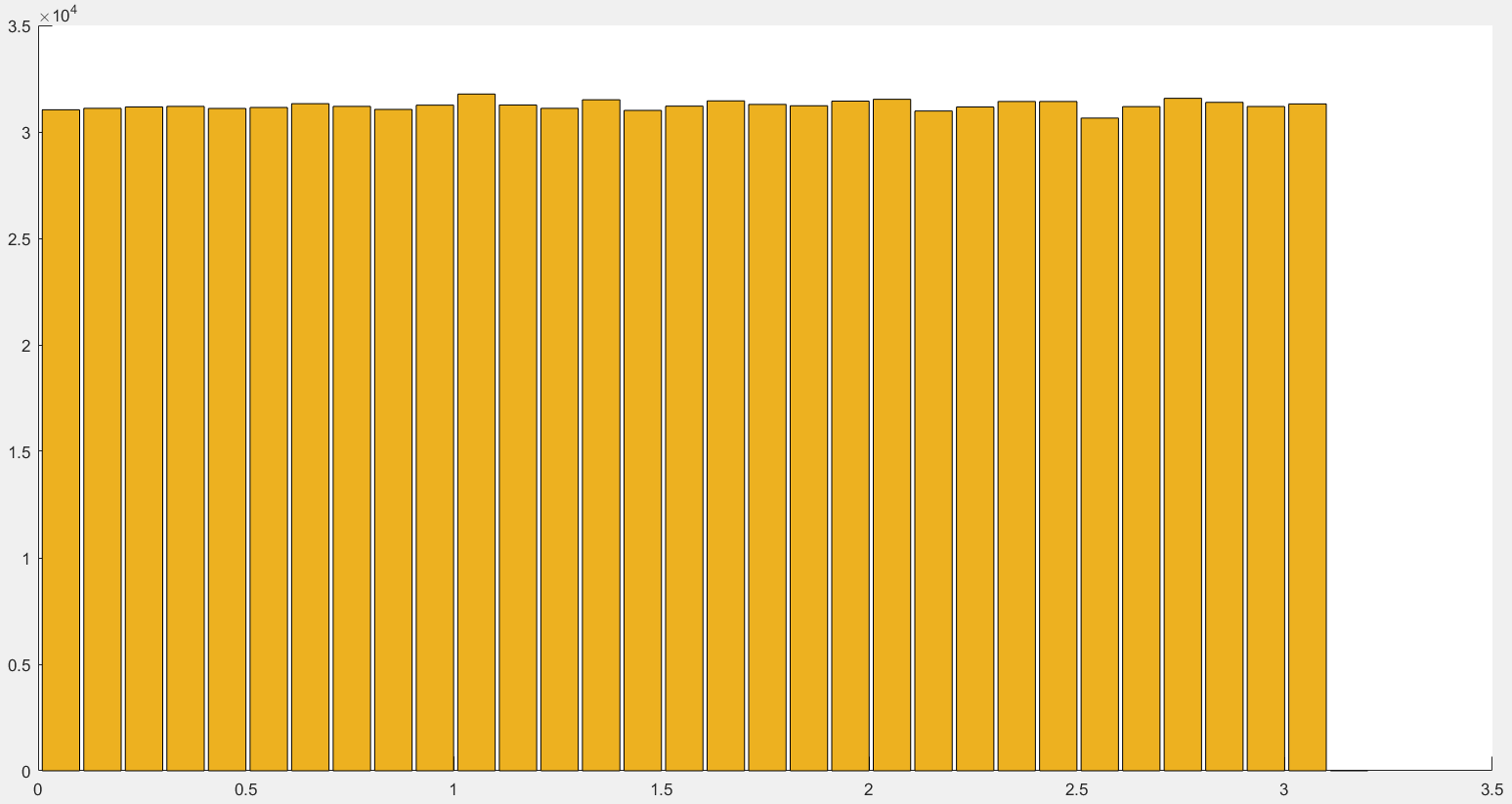
Рисунок 4 – Равномерное распределение
Для распределения Эрланга сведём все основные сведения в табл. 1:
|
|
|
|
|
|
|
|
Здесь
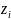 (
(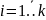 )
– это независимые реализации базовой
случайной величины. Пусть
)
– это независимые реализации базовой
случайной величины. Пусть
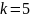 и
,
тогда теоретические моменты:
и
,
тогда теоретические моменты:
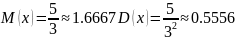
Эмпирические же оценки математического ожидания и дисперсии, полученные с помощью программы (рис. 5):
![]()
![]()
Рисунок 5 – Первый и второй моменты, вычисленные эмпирическим путём
Результаты обладают высокой точностью.
Гистограмма для данного распределения получилась следующая:
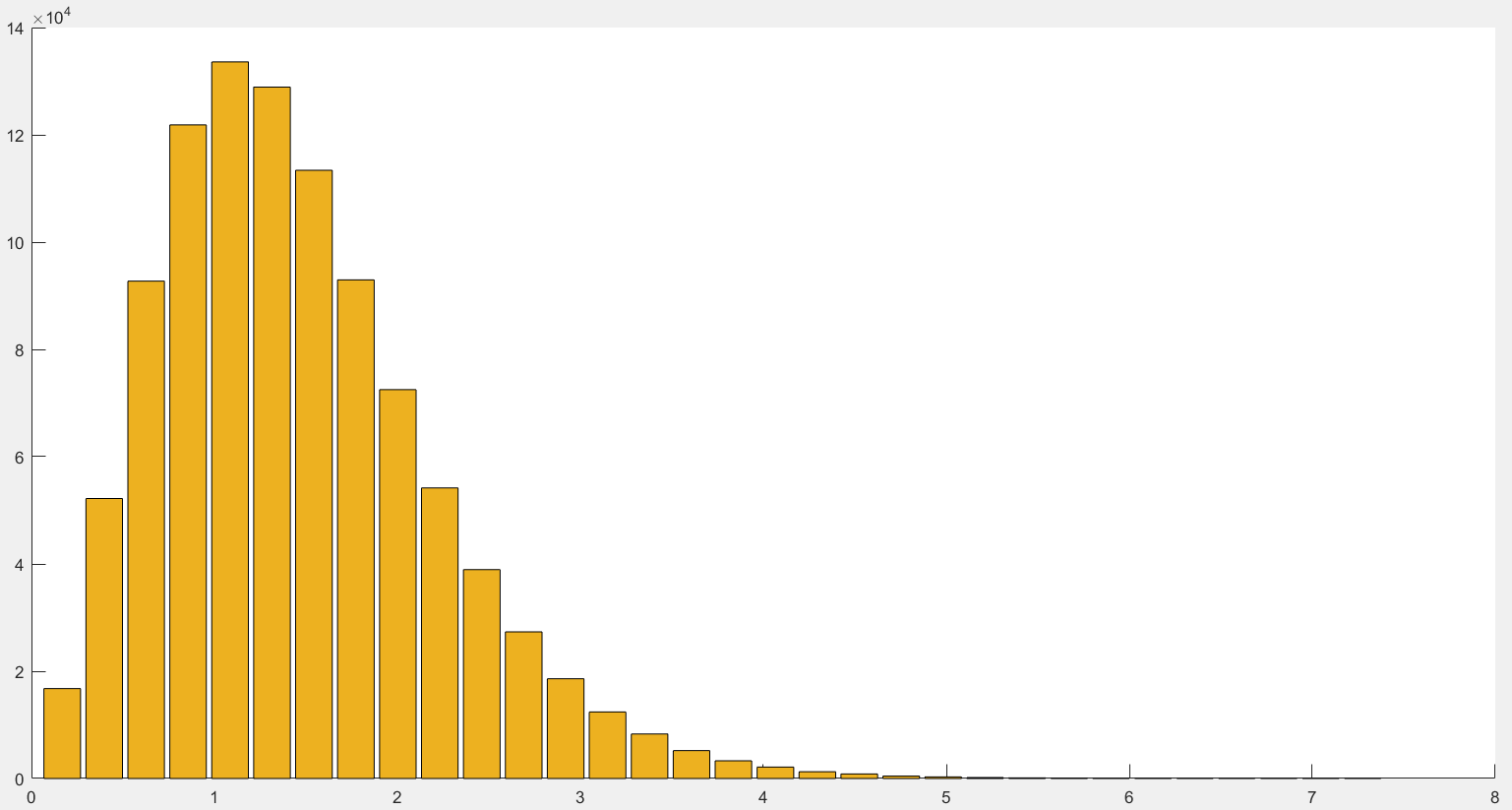
Рисунок 6 – Распределение Эрланга пятого порядка
Для нормального распределения сведём все основные сведения в табл. 2:
|
|
|
|
|
|
|
|
Но так как
аналитической функции, обратной функции
Лапласа, пока не выведено, будем искать
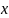 другим способом. Для реализации любой
нормальной случайной величины достаточно
иметь датчик стандартной (то есть
нормированной и центрированной)
нормальной случайной величины
другим способом. Для реализации любой
нормальной случайной величины достаточно
иметь датчик стандартной (то есть
нормированной и центрированной)
нормальной случайной величины
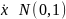 .
Чтобы реализовать случайную величину
𝑥
с нормальным распределением, используем
метод Бокса – Мюллера. Данный метод
позволяет получить два независимых
значения
.
Чтобы реализовать случайную величину
𝑥
с нормальным распределением, используем
метод Бокса – Мюллера. Данный метод
позволяет получить два независимых
значения
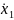 и
и
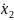 стандартной нормальной случайной
величины из двух независимых значений
стандартной нормальной случайной
величины из двух независимых значений
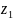 и
и
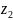 базовой случайной величины по формулам:
базовой случайной величины по формулам:

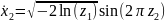
Причём в этих формулах и – две независимые реализации базовой случайной величины.
Теоретические значения и , как уже отмечалось, равны 0 и 1 соответственно.
Эмпирические же значения, по результатам работы программы, следующие (рис. 7):
![]()
![]()
Рисунок 7 – Первый и второй моменты, вычисленные эмпирическим путём
Гистограмма выглядит следующим образом:
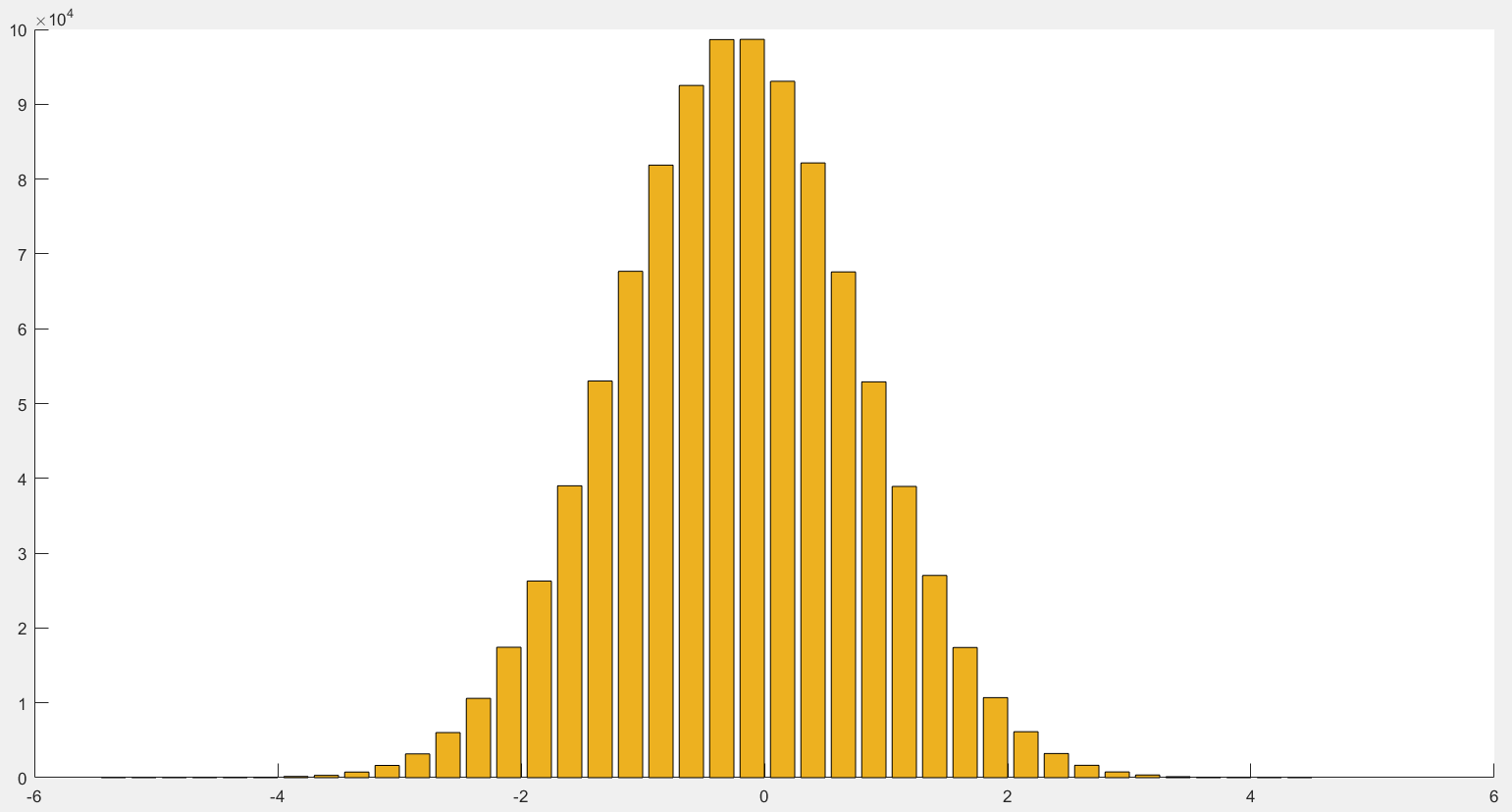
Рисунок 8 – Нормальное распределение
Для Парето распределения имеем следующие теоретические данные:
|
|
|
|
|
|
|
|
Важное замечание:
коэффициент
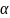 следует брать больше 2, так как при
следует брать больше 2, так как при
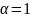 математическое ожидание, согласно
формуле, не определяется; для
математическое ожидание, согласно
формуле, не определяется; для
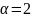 не определена дисперсия, что тоже можно
увидеть, взглянув на формулу. Итак, пусть
не определена дисперсия, что тоже можно
увидеть, взглянув на формулу. Итак, пусть
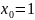 и
и
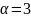 .
Тогда теоретические моменты:
.
Тогда теоретические моменты:
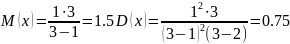
Эмпирические же значения, по результатам работы программы, следующие (рис. 9):
![]()
![]()
Рисунок 9 – Первый и второй моменты, вычисленные эмпирическим путём
Как видим, здесь уже точность немного упала для оценки математического ожидания. Значения дисперсии и вовсе расходятся чуть больше, чем на 0.06. Возможно, это связано с объёмом выборки, а вероятно, и с малым порядком, определяемым коэффициентом .
Гистограмма распределения Парето представлена на рис. 10:
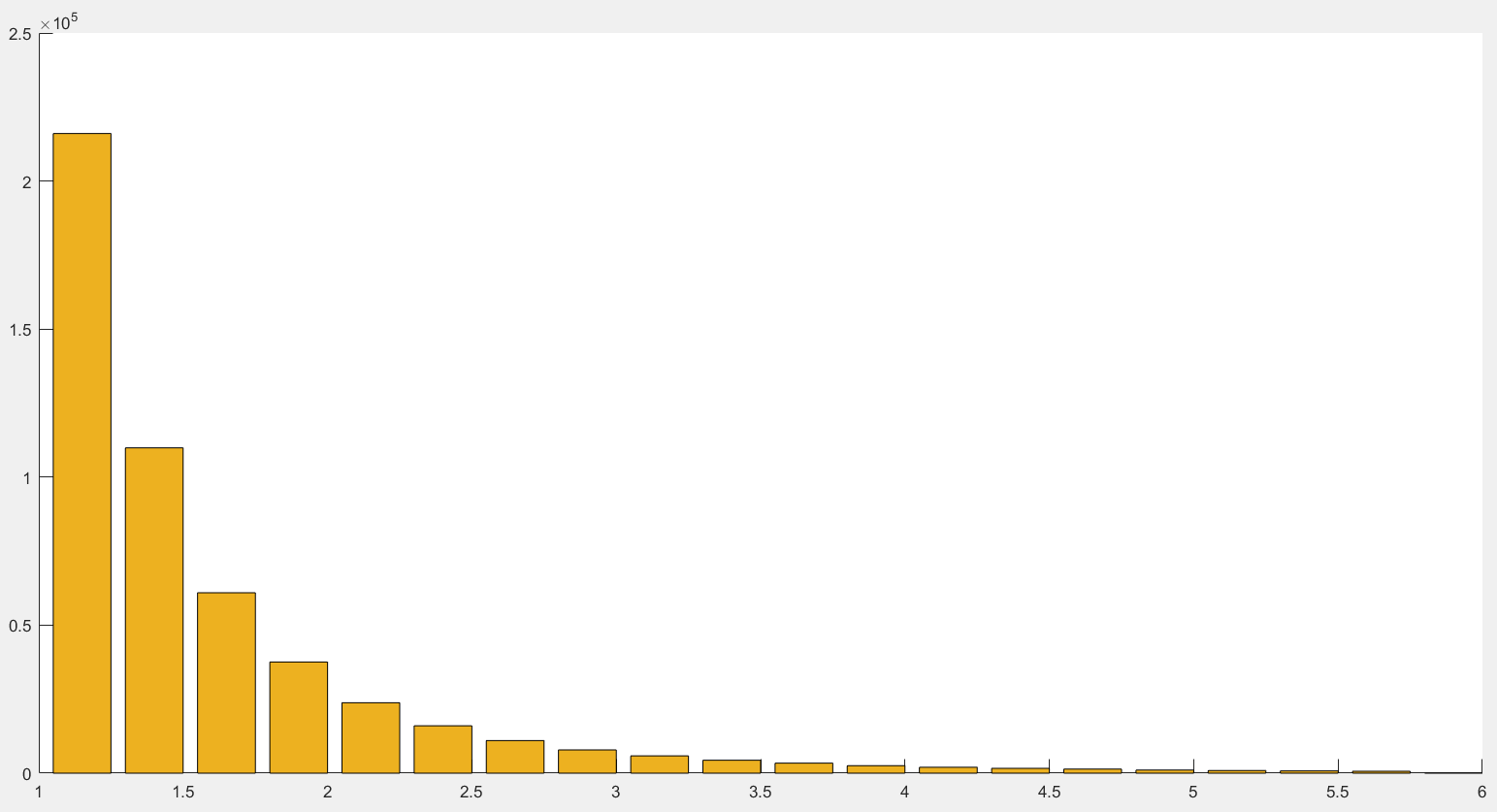
Рисунок 10 – Распределение Парето
Из рисунка видно, что Парето распределение очень похоже на экспоненциальное. Такой же вывод можно сделать, если посмотреть на функции распределений для экспоненциального и Парето.
Выводы.
В ходе работы была смоделирована базовая случайная величина. Моделирование происходило на пяти различных распределениях, что дало понять, насколько точные расчёты моментов были произведены во время моделирования.
Полный код программы.
Ниже приведён полный код программы. Для написания использовался пакет прикладных программ для решения задач технических вычислений MatLab.
clc; clear;
% формируем для датчика массив случайых чисел от 0 до 1
n = 1000000;
Zs = randi([0 100000], 1, n);
for i = 1 : n
if Zs(i) == 100000
Zs(i) = 0.9999;
else
Zs(i) = Zs(i) / 100000;
end;
end;
%% Экспоненциальное распределение
% Формируем массив для частот
N = 32;
Fs = zeros(1, N);
for i = 1 : N
Fs(i) = i * 0.05;
end;
% Считаем теоретические значения мат. ожидания и дисперсии
lambda = 3;
MXT = 1 / lambda;
DXT = MXT ^ 2;
% Формируем датчик БСВ
Xs = zeros(1, n);
for i = 1 : n
Xs(i) = -(1 / lambda) * log(1 - Zs(i));
end;
Xs = sort(Xs);
% Считаем частоты попадания в интервалы массива Fs
Ps = zeros(1, N);
for i = 1 : n
for j = 2 : N
if Xs(i) > Fs(j - 1) && Xs(i) <= Fs(j)
Ps(j - 1) = Ps(j - 1) + 1;
break;
end;
end;
end;
% Находим эмпирическое значение мат. ожидания
s = 0;
for i = 1 : n
s = s + Xs(i);
end;
MXR = s / n;
% Находим эмпирическое значение дисперсии
DXR = 0;
for i = 1 : n
DXR = DXR + Xs(i) ^ 2;
end;
DXR = DXR / n - MXR ^ 2;
% Строим гистограмму
for i = 1 : N
rectangle('Position', [Fs(i) - 0.05 0 0.05 Ps(i)], 'FaceColor', [0.9290 0.6940 0.1250]);
end
%% Равномерное распределение
% Формируем массив для частот и одноврменно диапазон [A; B]
A = 0;
N = 32;
Fs2 = zeros(1, N);
for i = 1 : N
Fs2(i) = i * 0.1;
end;
B = Fs2(N);
% Считаем теоретические значения мат. ожидания и дисперсии
MXT2 = (A + B) / 2;
DXT2 = ((B - A) ^ 2) / 12;
% Формируем датчик БСВ
Xs2 = zeros(1, n);
for i = 1 : n
Xs2(i) = A + Zs(i) * (B - A);
end;
Xs2 = sort(Xs2);
% Считаем частоты попадания в интервалы массива Fs
Ps2 = zeros(1, N);
for i = 1 : n
for j = 2 : N
if Xs2(i) > Fs2(j - 1) && Xs2(i) <= Fs2(j)
Ps2(j - 1) = Ps2(j - 1) + 1;
break;
end;
end;
end;
% Находим эмпирическое значение мат. ожидания
s2 = 0;
for i = 1 : n
s2 = s2 + Xs2(i);
end;
MXR2 = s2 / n;
% Находим эмпирическое значение дисперсии
DXR2 = 0;
for i = 1 : n
DXR2 = DXR2 + Xs2(i) ^ 2;
end;
DXR2 = DXR2 / n - MXR2 ^ 2;
% Строим гистограмму
for i = 1 : N
rectangle('Position', [Fs2(i) - 0.09 0 0.09 Ps2(i)], 'FaceColor', [0.9290 0.6940 0.1250]);
end
%% Распределение Эрланга порядка k
% Определяем параметры распределения
k = 5;
L = 3;
% Считаем теоретические значения мат. ожидания и дисперсии
MXT3 = k / L;
DXT3 = k / (L ^ 2);
% Формируем датчик БСВ
% Замечание: для случайной величины распределения Эрланга
% нам необходимы k случайных величин экспоненциального
% распределения
ExpXs = zeros(k, n);
Xs3 = zeros(1, n);
for l = 1 : k
Zs3 = randi([0 100000], 1, n);
for i = 1 : n
if Zs3(i) == 0
Zs3(i) = 0.0001;
else
Zs3(i) = Zs3(i) / 100000;
end;
end;
for i = 1 : n
ExpXs(l, i) = -(1 / L) * log(Zs3(i));
end;
end;
for i = 1 : n
for j = 1 : k
Xs3(i) = Xs3(i) + ExpXs(j, i);
end;
end;
Xs3 = sort(Xs3);
% Формируем массив для частот
start = min(Xs3);
finish = max(Xs3);
Fs3 = zeros(1, N);
for i = 1 : N
Fs3(i) = start + i * (finish - start) / N;
end;
% Считаем частоты попадания в интервалы массива Fs
Ps3 = zeros(1, N);
for i = 1 : n
for j = 2 : N
if Xs3(i) > Fs3(j - 1) && Xs3(i) <= Fs3(j)
Ps3(j - 1) = Ps3(j - 1) + 1;
break;
end;
end;
end;
% Находим эмпирическое значение мат. ожидания
s3 = 0;
for i = 1 : n
s3 = s3 + Xs3(i);
end;
MXR3 = s3 / n;
% Находим эмпирическое значение дисперсии
DXR3 = 0;
for i = 1 : n
DXR3 = DXR3 + Xs3(i) ^ 2;
end;
DXR3 = DXR3 / n - MXR3 ^ 2;
% Строим гистограмму
for i = 1 : N
rectangle('Position', [Fs3(i) - 0.2 0 0.2 Ps3(i)], 'FaceColor', [0.9290 0.6940 0.1250]);
end
%% Нормальное распределение
% Для моделирования используется слуайная величина стандартного
% нормального распределения, для которого М(Х) = 0 и D(Х) = 1
MXT4 = 0;
DXT4 = 1;
% формируем для датчика 1-й массив случайых чисел от 0 до 1
Zs4_u = randi([0 100000], 1, n);
for i = 1 : n
if Zs4_u(i) == 0
Zs4_u(i) = 0.0001;
else
Zs4_u(i) = Zs4_u(i) / 100000;
end;
end;
% формируем для датчика 2-й массив случайых чисел от 0 до 1
Zs4_v = randi([0 100000], 1, n);
for i = 1 : n
if Zs4_v(i) == 0
Zs4_v(i) = 0.0001;
else
Zs4_v(i) = Zs4_v(i) / 100000;
end;
end;
% Формируем датчик БСВ, используя метод
% Бокса - Мюллера (метод полярных координат)
Xs4 = zeros(1, n);
Ys4 = zeros(1, n);
for i = 1 : n
Xs4(i) = sqrt(-2 * log(Zs4_v(i))) * cos(2 * pi * Zs4_u(i));
Ys4(i) = sqrt(-2 * log(Zs4_v(i))) * sin(2 * pi * Zs4_u(i));
end;
% Формируем массив для частот
N = 40;
Fs4 = zeros(1, N);
for i = 1 : N
Fs4(i) = -5.5 + i * 0.25;
end;
% Считаем частоты попадания в интервалы массива Fs
Ps4 = zeros(1, N);
for i = 1 : n
for j = 2 : N
if Ys4(i) > Fs4(j - 1) && Ys4(i) <= Fs4(j)
Ps4(j - 1) = Ps4(j - 1) + 1;
break;
end;
end;
end;
% Находим эмпирическое значение мат. ожидания
s4 = 0;
for i = 1 : n
s4 = s4 + Ys4(i);
end;
MXR4 = s4 / n;
% Находим эмпирическое значение дисперсии
DXR4 = 0;
for i = 1 : n
DXR4 = DXR4 + Ys4(i) ^ 2;
end;
DXR4 = DXR4 / n - MXR4 ^ 2;
% Строим гистограмму
for i = 1 : N
rectangle('Position', [Fs4(i) - 0.2 0 0.2 Ps4(i)], 'FaceColor', [0.9290 0.6940 0.1250]);
end
%% Парето распределение
% Определяем параметры рапределения
% Замечание: так как для Парето распределения при alpha = 1
% мат. ожидание не определено, а при alpha = 2 не определена
% дисперсия, рассмариваем значения alpha > 2
X0 = 1;
alpha = 3;
% Формируем датчик БСВ
Xs5 = zeros(1, n);
for i = 1 : n
Xs5(i) = X0 / nthroot((1 - Zs(i)), alpha);
end;
% Считаем теоретические значения мат. ожидания и дисперсии
MXT5 = (alpha * X0) / (alpha - 1);
DXT5 = (alpha * (X0 ^ 2)) / ((alpha - 2) * ((alpha - 1) ^ 2));
% Находим эмпирическое значение мат. ожидания
s5 = 0;
for i = 1 : n
s5 = s5 + Xs5(i);
end;
MXR5 = s5 / n;
% Находим эмпирическое значение дисперсии
DXR5 = 0;
for i = 1 : n
DXR5 = DXR5 + Xs5(i) ^ 2;
end;
DXR5 = DXR5 / n - MXR5 ^ 2;
% Формируем массив для частот
N = 20;
Fs5 = zeros(1, N);
for i = 1 : N
Fs5(i) = X0 + i * 0.25;
end;
% Считаем частоты попадания в интервалы массива Fs
Ps5 = zeros(1, N);
for i = 1 : n
for j = 2 : N
if Xs5(i) > Fs5(j - 1) && Xs5(i) <= Fs5(j)
Ps5(j - 1) = Ps5(j - 1) + 1;
break;
end;
end;
end;
% Строим гистограмму
for i = 1 : N
rectangle('Position', [Fs5(i) - 0.2 0 0.2 Ps5(i)], 'FaceColor', [0.9290 0.6940 0.1250]);
end