9373_ЗаболотниковМЕ_ЛР_1
.docxМинистерство науки и высшего образования РФ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Информационных систем
отчёт
по лабораторной работе №1
по дисциплине «Моделирование систем массового обслуживания»
Тема: Базовая случайная величина
Студент гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Татарникова Т.М. |
Санкт-Петербург
2022
Цель работы.
Построить датчик базовой случайной величины по заданному алгоритму и выполнить тестирование датчика на соответствие основным свойствам базовой случайной величины.
Общие теоретические сведения.
Датчик базовой случайной величины (здесь и далее – БСВ), исследуемый в данной работе, – датчик "Little Frog". Описание данного датчика приведено ниже.
Сперва находим период последовательности БСВ:
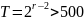
Затем
находится последовательность
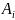длиной
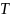по следующей формуле:
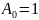
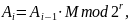
где
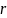– количество разрядов, используемых
для представления числа в компьютере,
а
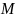– число, взаимно простое с
.
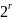Далее
последовательность
разбивается на подпоследовательности
,
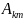каждая из которых состоит из
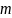элементов. Для первой такой
подпоследовательности состав следующий:
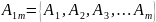
Каждая из последующих подпоследовательностей получается из предыдущей путём следующей операции над каждым её элементом:
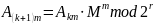
В итоге
имеем
подпоследовательностей длины
.
Теперь из полученных подпоследовательностей
получаем сами значения БСВ:
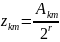
Ход работы.
Известно,
что для представления числа в компьютере
используется 8, 16, 32 или 64 бита, в зависимости
от типа. Для нашей работы возьмём
.
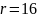Тогда:
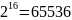
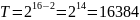
В
качестве множителя
возьмём число 101, которое является
простым, следовательно – взаимно просто
с 65536, так как последнее не имеет числа
101 среди своих делителей. Также, возьмём
.
Ниже представлен кусок кода, отвечающий за построение датчика БСВ:
for i = 2 : n
A(i) = A(i - 1) * M;
A(i) = mod(A(i), 65536);
if A(i) == A(1)
period = period + 1;
end;
end;
Akm(1, 1) = A(1);
Akm(2, 1) = A(2);
Akm(3, 1) = A(3);
Akm(4, 1) = A(4);
for i = 2 : seqs_num
for j = 1 : m
Akm(j, i) = Akm(j, i - 1) * (M ^ m);
Akm(j, i) = mod(Akm(j, i), 65536);
end;
end;
k = 0;
for i = 1 : seqs_num
for j = 1 : m
Z(k + j) = Akm(j, i) / (2 ^ r);
end;
k = k + 4;
end;
После
того, как датчик построен, посчитаем
математическое ожидание
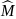и дисперсию
ряда псевдослучайных чисел
.
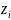Для этого воспользуемся следующими
формулами нахождения этих величин
соответственно:
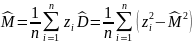
Теоретические
значения
и
равны соответственно
и
,
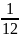что в переводе в десятичные дроби
выглядит следующим образом:
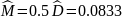
Программа выдаёт следующие значения:
Если мы сравним эти значения с теоретическими, то убедимся, что выборка , а значит, и датчик БСВ, удовлетворяет свойствам равномерности.
Теперь
проверим свойство равномерности датчика
другим способом – частотным методом.
Для этого разобьём отрезок
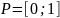на
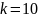равных интервалов и построим гистограмму
относительных частот
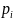на этом отрезке. Получаем следующий
результат:
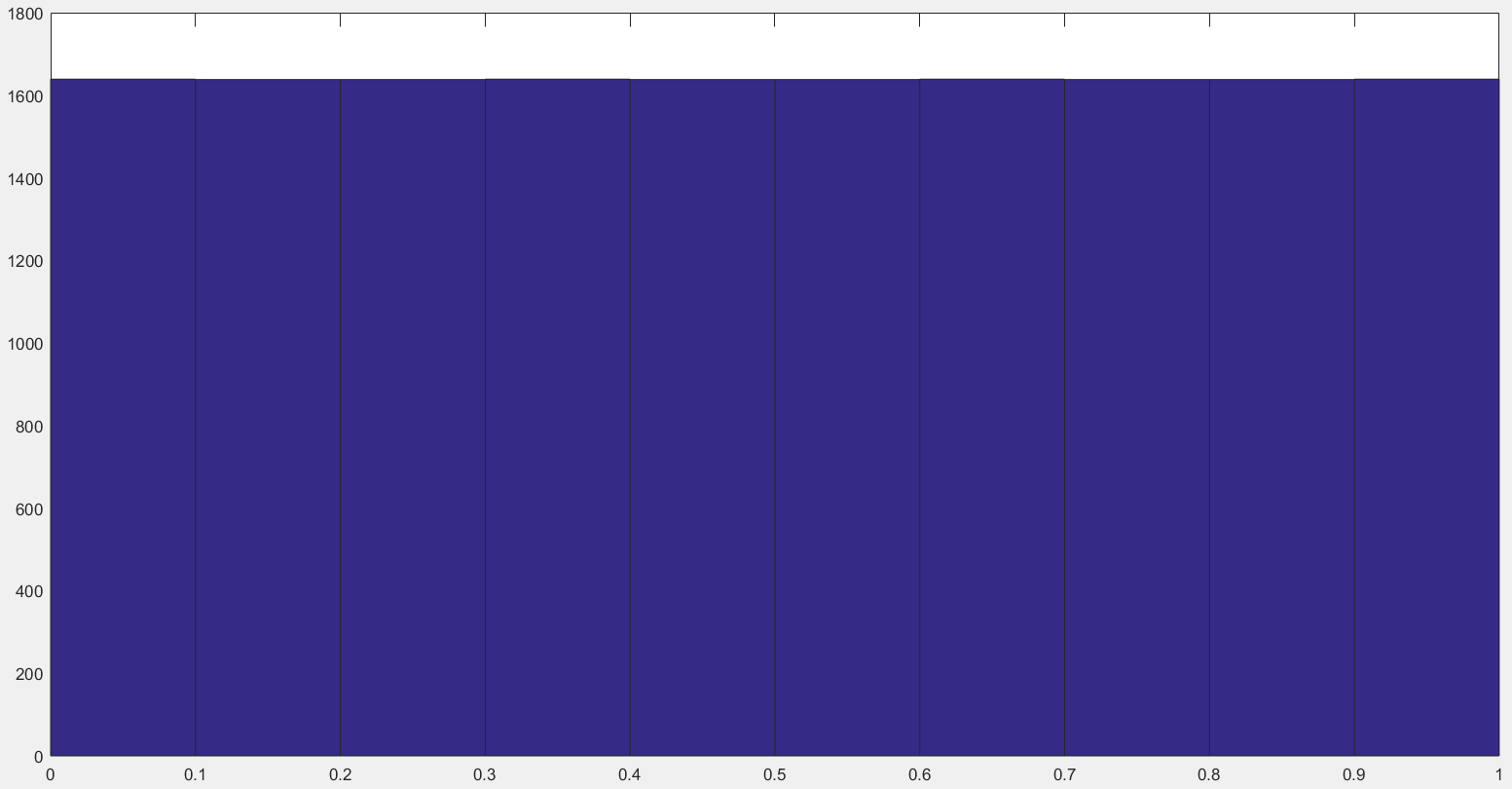
Данная гистограмма наглядно демонстрирует выполнение датчиком свойства равномерности. Дополнительно свойство равномерности демонстрируется диаграмма распределения БСВ:
И в
конце проверим наш датчик БСВ на
независимость, определяя коэффициент
корреляции для разных значени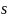й
и
:
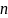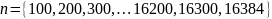
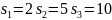
Для
расчёта самого коэффициента корреляции
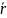будем использовать формулу:
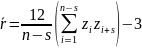
После
проведённых расчётов построим графики
зависимостей
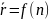для
,
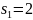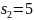и
:
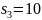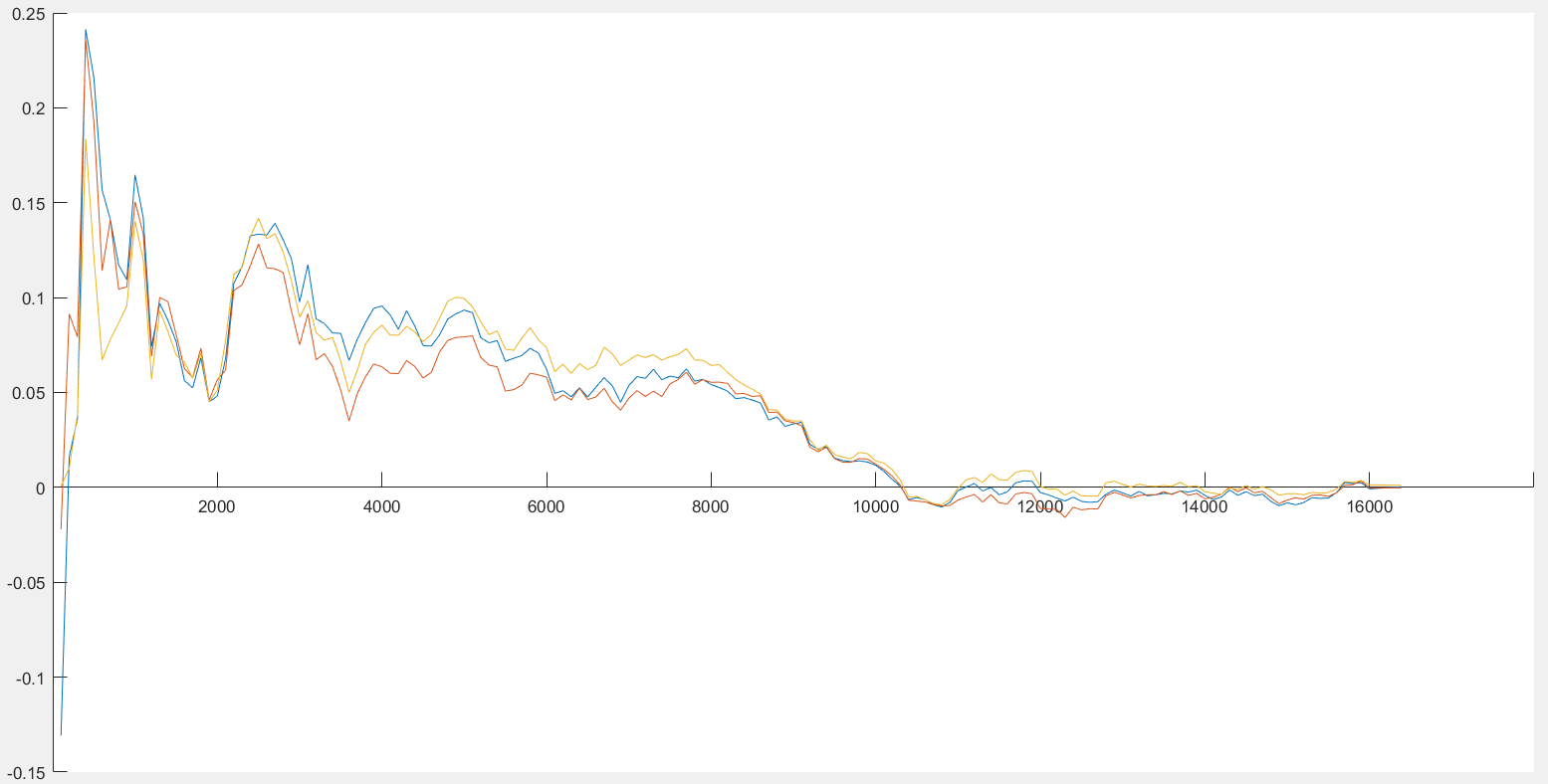
На
рисунке синий график соответствует
вычислениям при
,
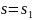красный – вычислениям при
,
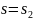а оранжевый – при
.
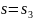Из рисунка понятно, что при увеличении
объёма выборки
линейная зависимость между
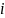-тым
и
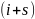-м
элементами выборки выражается всё в
меньшей и меньшей степени.
Выводы.
В ходе данной работы по заданному алгоритму был построен датчик базовой случайной величины "Little Frog". Путём двух вариантов тестирования датчика на обладание им свойства равномерности убедились, что такой датчик удовлетворяет этому свойству.
Кроме того, изучили свойство независимости исследуемой БСВ через вычисление коэффициента корреляции при различных объёмах выборки и различных параметрах . Убедились в том, что с возрастанием объёма выборки элементы этой выборки всё в меньшей степени обладают линейной зависимостью.
Полный код программы.
Ниже приведён полный код программы. Для написания использовался пакет прикладных программ для решения задач технических вычислений MatLab.
clc; clear;
r = 16;
T = 16384;
ns = zeros(1, 161);
for i = 1 : 160
ns(i) = i * 100;
end;
ns(161) = T;
s1 = 2;
s2 = 5;
s3 = 10;
s = s3;
Rs = zeros(1, 161);
for l = 1 : 161
n = ns(l);
A = zeros(1, n);
m = 4;
M = 101;
A(1) = 1;
period = 0;
seqs_num = n / m;
Akm = zeros(4, seqs_num);
Z = zeros(1, n);
for i = 2 : n
A(i) = A(i - 1) * M;
A(i) = mod(A(i), 65536);
if A(i) == A(1)
period = period + 1;
end;
end;
Akm(1, 1) = A(1);
Akm(2, 1) = A(2);
Akm(3, 1) = A(3);
Akm(4, 1) = A(4);
for i = 2 : seqs_num
for j = 1 : m
Akm(j, i) = Akm(j, i - 1) * (M ^ m);
Akm(j, i) = mod(Akm(j, i), 65536);
end;
end;
k = 0;
for i = 1 : seqs_num
for j = 1 : m
Z(k + j) = Akm(j, i) / (2 ^ r);
end;
k = k + 4;
end;
MZ = sum(Z) / n;
DZ = 0;
for i = 1 : n
DZ = DZ + Z(i) ^ 2 - MZ ^ 2;
end;
DZ = DZ / n;
Xs = zeros(0, n);
for i = 1 : n
Xs(i) = i;
end;
scatter(Xs, Z, '.');
hist(Z);
Z = sort(Z);
MZZ1 = 0;
MZZ2 = 0;
MZZ3 = 0;
for i = 1 : (n - s)
MZZ1 = MZZ1 + Z(i) * Z(i + s);
end;
Rs(l) = MZZ1 / (n - s);
Rs(l) = Rs(l) * 12;
Rs(l) = Rs(l) - 3;
end;
hold on;
set(gca, 'XAxisLocation', 'origin');
plot(ns, Rs);