ПР7_Заболотников_9373

Цель работы.

Освоение основных понятий и некоторых методов кластерного анализа, в

частности, метода поиска сгущений.

Основные теоретические положения.

Для выполнения данной практической работы были использованы

следующие понятия и формулы.

1.Кластерный анализ – задача разбиения заданной выборки объектов объёма на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались друг от друга.

2.Метрика – неотрицательная вещественная функция ( , ), которая называется функцией расстояния, если:

a)( , ) ≥ 0;

b)( , ) = ( , );

c)( , ) ≤ ( , ) + ( , ).

3.Метод FOREL (метод поиска сгущений) заключается в поиске скоплений точек множества. В качестве границ этих скоплений будет вступать окружность радиуса – радиус поиска локальных сгущений.

Суть метода в следующем. Пусть имеется множество точек , которое необходимо кластеризовать. Объём этого множества: . Зададим радиус окружности – радиус поиска локальных сгущений . Осуществляем следующие действия:

a)Выделяем некоторое множество из – множество некластеризованных точек: ;

b)В полученном множестве выбираем некоторую точку – центроид 0:

0 ;

c)В текущий кластер помещаем все точки, находящиеся на расстоянии от

0, меньшем либо равным, чем : { |( , 0) ≤ };

2

d) В текущем кластере пересчитываем центр масс : = 1 ∑ ;

| |

e)Проверяем: если 0 ≠ , то новым центроидом текущего кластера становится точка : 0 . Потом переходим к п. c. Будем проходить п. c – e до тех пор, пока очередное 0 не станет равно рассчитанному . Когда это случилось, переходим к п. f;

f)"Выбрасываем" из все те точки, которые остались в текущем кластере: \ ;

g)Проходим п. b – f до тех пор, пока в имеются свободные

(некластеризованные) точки, то есть пока | | > 0. Алгоритм же

завершит свою работу, когда множество опустеет.

Метрика, используемая в методе, – евклидово расстояние:

( , ) = √∑( − )2

=1

При выборе радиуса важно учитывать, что границы нашей окружности не должны превышать размеры разброса значений выборки: в противном случае мы сможем разделить наше множество лишь на один единственный кластер – само это множество, – а в этом нет никакого смысла. С другой стороны, если радиус окружности будет меньше, чем минимальное возможное расстояние между любыми двумя точками выборочной совокупности, то тогда кластеров будет ровно столько, сколько элементов в этой совокупности. Такое разбиение тоже не принесёт никакой практической пользы. Получается, радиус окружности должен лежать в промежутке от до , где

= { ( , )}

= { ( , )},

то есть < < .

Также необходимо понимать, что от выбранного радиуса окружности зависит количество кластеров, на которые алгоритм поиска сгущений разобьёт

3

исходное множество. Так, чем меньше R, тем больше кластеров получится в итоге.

Постановка задачи.

Дано конечное множество из объектов, представленных двумя признаками (в качестве этого множества принимаем исходную двумерную выборку, сформированную ранее в практической работе №4). Выполнить разбиение исходного множества объектов на конечное число подмножеств (кластеров) с использованием метода поиска сгущений. Полученные результаты содержательно проинтерпретировать.

Исходные данные – двумерная выборка, а также некоторые данные из предыдущих работ. Программный код представлен в приложении А.

Выполнение работы.

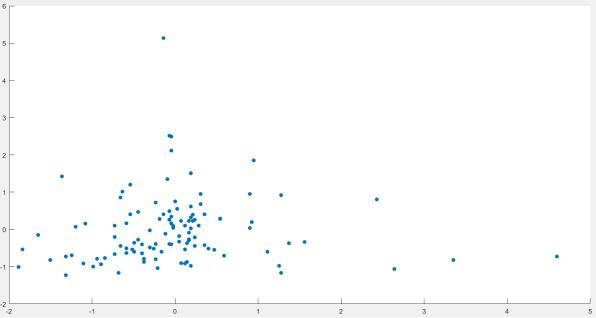
В первую очередь, воспользуемся нормализованной выборкой из предыдущей практической работы (см. рис. 1):

Рисунок 1 – Нормализованная двумерная выборка на графике Теперь, используя алгоритм поиска сгущений, разобьём выборку на

кластеры. Так как наибольшее расстояние между двумя точками выборки точно

больше 1 (это видно на рис. 1), а наименьшее явно меньше 0.5 (что тоже понятно

4

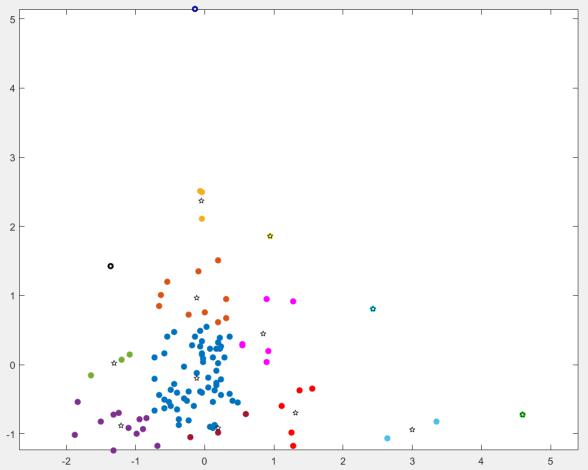
из рис. 1), положим радиус = 0.8. Выполним алгоритм FOREL, а результаты представим на рис. 2:

Рисунок 2 – Результат работы алгоритма FOREL (центроиды кластеров обозначены звёздочками)

Из рисунка понятно, что алгоритм разбил нашу выборку на 14 кластеров.

Теперь проверим чувствительность алгоритма к погрешностям: изменим радиус поиска локальных сгущений, увеличив и уменьшив его на 0.00001. Посмотрим,

как изменится (и изменится ли вообще) количество кластеров. Результаты представим на рис. 3 и рис. 4:

5

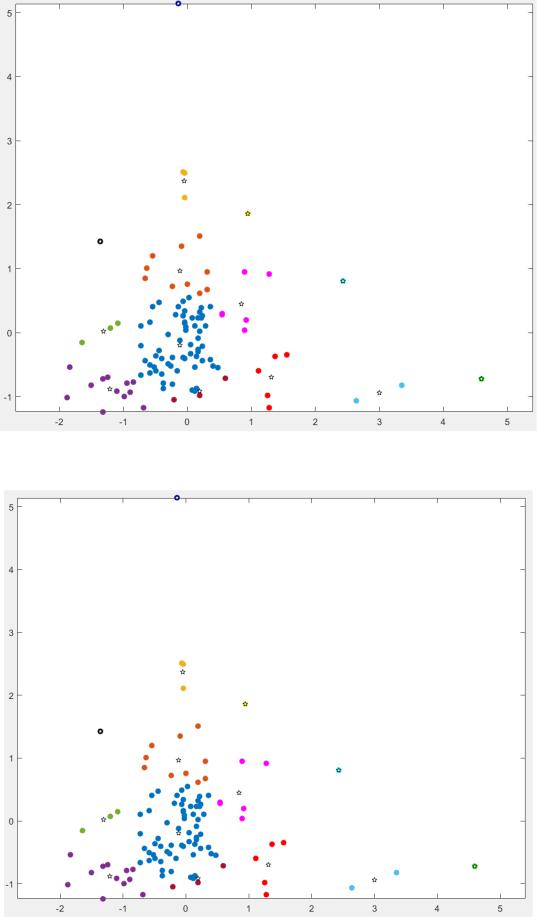
Рисунок 3 – Результат выполнения алгоритма при = 0.80001

Рисунок 4 – Результат выполнения алгоритма при = 0.79999

6

Судя по рис. 3 и рис.4, изменение радиуса поиска сгущений на столь малое

значение никак не повлияло на результат выполнения алгоритма.

Ив конце, используя данные предыдущей практической работы, сравним

иоценим качество разбиения на кластеры метода FOREL с методами k-means и

k-medoids. Результаты сведём в табл. 1:

Таблица 1 – Оценка качества кластеризации

Таким образом, мы понимаем, что метод FOREL далеко не лучший среди своих конкурентов.

Сравнивая метод FOREL с методами k-means и k-medoids, мы можем сделать вывод, что успешность этого метода зависит от выбора начального центроида. Это легко понять, если взглянуть ещё раз, например, на рис. 2. Видно,

что существуют некоторые точки, которые попали не в "свой" кластер. Это произошло потому, что они после того, как попали в какой-то кластер,

вычёркиваются из рассмотрения дальше, хотя, возможно, логичнее было бы их отнести к другим кластерам. Таким недостатком не страдают остальные методы.

Однако, преимущество метода FOREL заключается в том, что здесь нам заранее не известно количество кластеров, поэтому появляется возможность распределять точки более точным образом.

Выводы.

7

В ходе работы был освоен такой метод кластеризации, как метод поиска сгущений (метод FOREL). Выяснилось, что, несмотря на, на первый взгляд,

более детальное разбиение на кластеры ввиду не известного заранее количества кластеров, данный метод не очень точно выполняет свою работу, что стало понятно благодаря некоторым точкам выборки, которые попали не в свой кластер.

На основе двух последних практических работ можно сделать вывод, что среди методов k-means, k-medoids, k-means++ и FOREL, лучше всех со своей задачей справляется метод k-means++.

8

ПРИЛОЖЕНИЕ А

ПРОГРАММЫЙ КОД (ЯЗЫК ПРОГРАММИРОВАНИЯ – MATLAB)

%%Исходные данные clear; clc;

X_ORIG = [97 102 83 90 102 109 108 98 107 53 54 77 ...

94 84 212 71 105 98 79 90 62 108 153 69 60 58 ...

91 64 97 75 95 154 242 295 87 94 203 22 96 103 ...

138 140 138 89 20 81 30 72 112 158 125 36 77 154 ...

107 99 44 47 120 108 115 75 97 44 78 110 101 98 ...

105 84 73 108 106 106 107 105 110 98 72 83 87 79 ...

107 109 113 110 100 92 81 75 93 123 139 115 97 69 ...

49 108 166 69 123 147 42 75 117 103 98 98 90 99 113]; Y_ORIG = [63 67 62 63 76 112 182 220 102 30 97 113 ...

113 38 21 14 30 109 50 37 29 26 26 46 38 25 ...

22 39 118 48 80 14 36 42 86 410 138 54 172 31 147 ...

204 90 55 24 70 78 141 94 64 43 36 163 145 69 90 ...

42 44 53 89 61 48 245 10 54 60 122 62 54 33 151 126 ...

64 33 82 94 74 244 60 47 57 65 71 102 130 104 135 105 ...

117 56 50 105 100 113 104 75 92 108 66 94 106 50 177 ...

98 55 102 98 97 133 93 147]; X_AVR = 99.898648648648650; Y_AVR = 87.477477477477490; CORR_STDX = 42.429909837167640; CORR_STDY = 62.765142489764250; n = 111;

%%Пункт 1. Нормирование точек

% Нормирование

X_NORM = randi(1, 1, n); Y_NORM = randi(1, 1, n); for i = 1 : n

X_NORM(i) = (X_ORIG(i) - X_AVR) / CORR_STDX;

Y_NORM(i) = (Y_ORIG(i) - Y_AVR) / CORR_STDY;

end;

% Отображение

scatter(X_NORM, Y_NORM, 'filled');

%% Пункт 2. Метод поиска сгущений

CLASTERS = zeros(n); CENTROIDS = zeros(2, n); R = 0.8;

% R = 0.80001; R = 0.79999; - это для проверки чувствительности

U = zeros(1, (n + 1)); for i = 1 : n

U(i) = i;

end; rev2 = 1; r = 1;

v = n; while(rev2 ~= 0)

x0 = X_NORM(U(1));

y0 = Y_NORM(U(1)); CURR_CL = zeros(1, n);

9

v = 1; while(U(v) ~= 0)

v = v + 1;

end;

v = v - 1; rev = 0;

while(rev == 0) for i = 1 : n

CURR_CL(i) = 0;

end; j = 1;

for i = 1 : v

d_x = (X_NORM(U(i)) - x0) ^ 2; d_y = (Y_NORM(U(i)) - y0) ^ 2; d = sqrt(d_x + d_y);

if(d <= R)

CURR_CL(j) = U(i); j = j + 1;

end;

end; i = 1;

while(CURR_CL(i) ~= 0) i = i + 1;

end;

k = i - 1; mass_center_x = 0; mass_center_y = 0; for i = 1 : k

mass_center_x = mass_center_x + X_NORM(CURR_CL(i)) /

k;

mass_center_y = mass_center_y + Y_NORM(CURR_CL(i)) /

k;

end;

if(mass_center_x ~= x0 || mass_center_y ~= y0) x0 = mass_center_x;

y0 = mass_center_y;

else

rev = 1;

end;

end;

i = 1; while(CURR_CL(i) ~= 0)

CLASTERS(r, i) = CURR_CL(i); i = i + 1;

end;

CENTROIDS(1, r) = x0; CENTROIDS(2, r) = y0; r = r + 1;

U_save = zeros(1, v); for i = 1 : n

U_save(i) = U(i); U(i) = 0;

end;

10