ПР6_Заболотников_9373

Цель работы.

Освоение основных понятий и некоторых методов кластерного анализа, в

частности, метода k-means.

Основные теоретические положения.

Для выполнения данной практической работы были использованы следующие понятия и формулы.

1. Нормализация множества точек – процесс преобразования множества точек, описывающийся формулой:

и– исправленное СКО признака.

2.Кластерный анализ – задача разбиения заданной выборки объектов объёма на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались друг от друга.

3.Метрика – неотрицательная вещественная функция ( , ), которая называется функцией расстояния, если:

a)( , ) ≥ 0;

b)( , ) = ( , );

c)( , ) ≤ ( , ) + ( , ).

4.Метод k-means (метод k-средних) заключается в минимизации СКО точек внутри кластеров от центров этих кластеров.

Критерием выступает минимальное расстояние внутри кластера относительно среднего.

Идея метода: на каждой итерации пересчитывается центр масс для каждого кластера, полученного на предыдущем шаге, а потом происходит разбиение на кластеры.

Метрика, используемая в методе, – евклидово расстояние:

2

=1

Шаги алгоритма:

a)Выбираем точек (количество кластеров), являющихся начальными центроидами.

b)Отнести каждый объект к кластеру с ближайшим центроидом.

c)Пересчитать центроиды кластеров согласно текущему членству.

d)Если критерий остановки алгоритма не удовлетворён, то необходимо перейти к п. b. Критерий остановки алгоритма: все значения текущего набора центроидов равны значениям предыдущего набора.

5.Метод k-medoids – использует для представления центра кластера не

центр масс, а представительный объект – один из объектов кластера. Каждый из оставшихся объектов объединяется в кластеры с ближайшим медоидом,

используя любые распространённые методы изменения расстояния. Далее необходимо выполнять алгоритм, пока стоимость выбора нового медоида снижается. Необходимо определить точку, принадлежащую кластеру,

расстояния которой до всех других точек кластера минимальны.

6. Определение верхней оценки количества кластеров определяется по формуле:

помощью метода локтя:

– центр кластера.

3

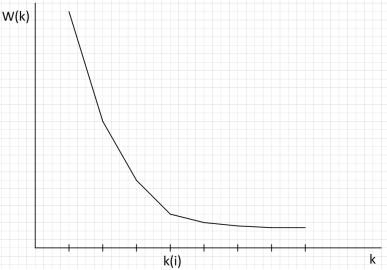
По полученным значениям строится график зависимости ( ),

который выглядит примерно так (см. рис. 1):

Рисунок 1 – Иллюстрация метода локтя Чтобы определить оптимальное значение количества кластеров ,

необходимо на найти точку , в которой график сильнее всего изгибается.

Иными словами, необходимо определить, при каком количестве кластеров последний разброс будет убывать с наименьшей степенью. Это и будет оптимальное значение .

8. Существует улучшенная модификация алгоритма k-means: k- means++. Суть улучшения заключается в нахождении более хороших начальных значений центроидов. Ведь в классическом k-means начальные центроиды выбираются случайно. Основная часть алгоритма ничем не отличается от его классического брата k-means. Различие состоит в выборе начальных центроидов.

Вот как это происходит:

a)Первый центроид выбирается случайным образом среди всех точек.

b)Для каждой точки находится квадрат расстояния до ближайшего

центроида (из тех, что уже выбраны) 2( , ).

c) Каждый новый центроид (начиная со второго) определяется таким образом, чтоб вероятность выбора точки была пропорциональна

рассчитанному для неё квадрату расстояния 2( , ). Чтобы это сделать,

будем складывать все найденные 2 для каждой точки. Потом сгенерируем

4

случайное значение (0, 1). Число = ∙ ∑ 2 будет лежать в интервале

(0, ∑ 2). Теперь определим новый центроид. Для этого начнём опять суммировать все 2 до тех пор пока сумма не будет превышать . Как только наша сумма переступит этот порог, суммирование прекращается и мы берём текущую точку в качестве нового центроида.

d) Будем повторять шаги b и c, пока не найдём все центроиды. Ну а дальше выполняется основная часть алгоритма k-means.

9. Можно провести оценку качества разбиения на кластеры. Для этого посчитаем следующую суму:

=1

где | | – количество элементов в -ом кластере, а – сумма расстояний вот всех точек -го кластера до его центроида:

| |

=1

Чем меньше , тем меньше , а значит, лучше работа того или иного метода кластеризации.

Постановка задачи.

Дано конечное множество из объектов, представленных двумя признаками (в качестве этого множества принимаем исходную двумерную выборку, сформированную ранее в практической работе №4). Выполнить разбиение исходного множества объектов на конечное число подмножеств (кластеров) с использованием метода k-means. Полученные результаты содержательно проинтерпретировать.

Исходные данные – значения, полученные в предыдущих практических работах. Программный код представлен в приложении А.

5

Выполнение работы.

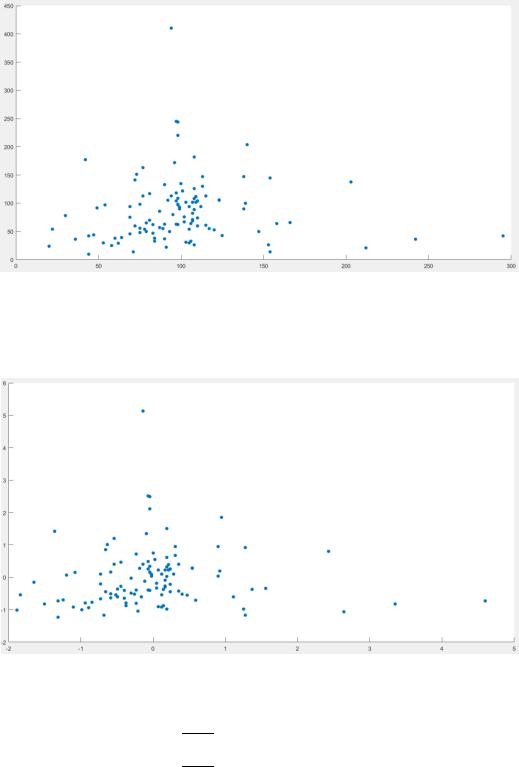
В первую очередь, построим нашу двумерную выборку и отобразим её на графике. Для этого обозначим на координатной плоскости все точки с координатами ( , ). Результат представлен на рис. 2:

Рисунок 2 – Двумерная выборка на графике Теперь нормализуем наше множество точек, используя формулу (1).

Получим то же рассеяние, только в меньших масштабах (см. рис. 3):

Рисунок 3 – Нормализованная двумерная выборка на графике Далее по формуле (3) определим верхнюю оценку количества кластеров :

111= √ 2 ≈ 7.4498 = 7

6

Это значит, что делить наше множество больше, чем на 7 кластеров, не имеет смысла.

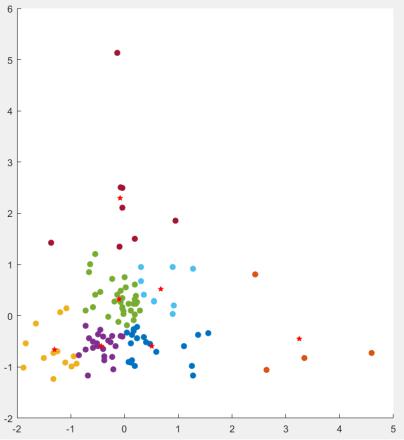
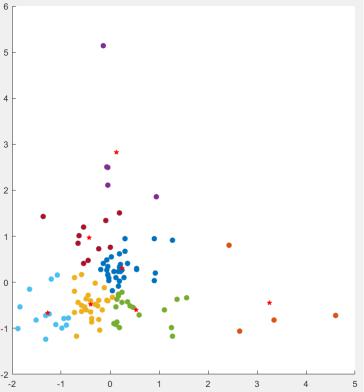
Теперь, используя алгоритм k-means, разделим наше множество на кластеры. Результат работы алгоритма представлен на рис. 4:

Рисунок 4 – Получившиеся кластеры (центры кластеров отмечены красными звёздочками)

Теперь попробуем разделить наш множество на кластеры путём применения метода k-medoids. Результат разбиения представим на рис. 5:

7

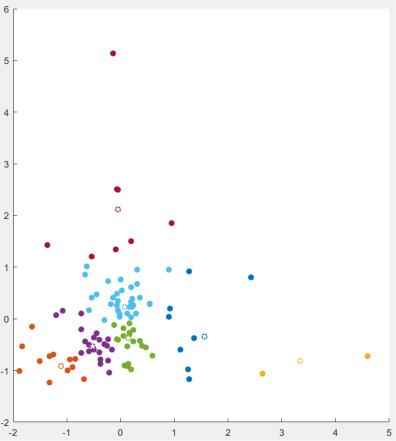
Рисунок 5 – Результат работы алгоритма k-medoids (центры кластеров отображены в виде белых звёздочек)

Далее определим оптимальное количество интервалов . Для того

воспользуемся методом локтя и посчитаем все значения при ̅̅̅̅̅. График

= 1, 7

зависимости ( ) представлен на рис. 6. На рис. 6: график с зелёными точками

– это результат работы метода локтя для алгоритма k-means, график с чёрными точками – для алгоритма k-medoids.

8

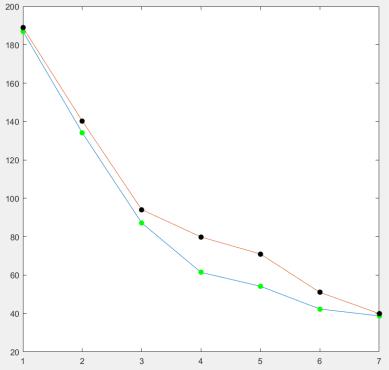
Рисунок 6 – Иллюстрация метода локтя

Как видно из рисунка, для метода k-means оптимальным количеством будет = 4, для метода k-medoids – = 3.

Как видим, оба метода справляются с разбиением множества на кластеры.

Теперь, используя формулы (5) и (6), проверим качество разбиения на кластеры,

результаты сведём в табл. 1:

Таблица 1 – Оценка качества кластеризации

9

Исходя из информации в таблице, можем сделать вывод, что метод k-means

сзадачей кластеризации справился лучше, чем метод k-medoids.

Ив конце реализуем модификацию алгоритма: k-means++. Возьмём случайную точку, пусть это будет точка (−0.0683, −0.3900). После работы алгоритма получится такая картина (см. рис. 7):

Рисунок 9 – Результат работы k-means++

Выводы.

В ходе работы были освоены основные понятия и некоторые методы кластерного анализа, в частности, метод k-means. Также были выполнены поставленные задачи на основании проведённых оценок качества работы алгоритмов сделан вывод о том, что наилучшим методом кластеризации является метод k-means. Кроме всего прочего, была реализована модификация метода k- means – k-means++. В сравнении со своей классической версией он работает лучше, так как начальные центроиды выбираются по определённым правилам, а

значит, эти центроиды более удачные.

10