ПР3_Заболотников_9373

Цель работы.

Получение практических навыков вычисления интервальных статистических оценок параметров распределения выборочных данных и проверки «справедливости» статистических гипотез.

Основные теоретические положения.

Для выполнения данной лабораторной работы были использованы следующие понятия и формулы.

1.Интервальная оценка параметра – оценка, определяемая двумя числами: границами интервала.

2.Пусть – оценка параметра . Чем меньше | − |, тем точнее оценка . Тогда некоторая величина > | − | характеризует точность оценки.

3.Надёжность (доверительная вероятность) оценки по –

вероятность , при которой | − | < . Иными словами, = (| − | < ),

т. е.

при неизвестном среднеквадратичном отклонении и заданном объёме выборки вычисляются следующим образом:

для правой границы.

В этих формулах – это и есть та самая точность, которая вычисляется по формуле:

√

2

где – исправленное СКО, – объём выборки, а – коэффициент Стьюдента,

значения которого зависят от и от . Значения этого коэффициента табулированы.

6. Для нахождения доверительного интервала для СКО при известном

исправленном СКО с заданной надёжностью используются следующие формулы:

для правой. Значения зависят от и от , и они табулированы.

7.Статистическая гипотеза – предположение о генеральной совокупности, проверяемое по выборке.

8.Статистический критерий – критерий, по которому принимается или опровергается гипотеза.

9.Пусть 0 – нулевая (изначальная) гипотеза, а 1 – альтернативная

(конкурирующая) гипотеза. Тогда (уровень значимости критерия) –

вероятность принять альтернативную гипотезу (или опровергнуть нулевую):

= (1/0)

10.Эмпирические частоты – абсолютные частоты ( ), наблюдаемые в эксперименте.

11.Точечная вероятность – вероятность того, что (−1; ], которая рассчитывается следующим образом:

где – выборочное среднее, – выборочное СКО (или исправленное СКО), а

Φ( ) – значение функции Лапласа.

12. Выравнивающая (теоретическая частота) – величина, которая находится по формуле:

где – объём выборки, а – точечная вероятность.

3

где – количество интервалов.

14.Число степеней свободы – величина, которая вычисляется так:

где – число параметров дифференциальной функции распределения. Для нормального распределения = 2, поэтому:

15. Критерий 2 (Пирсона) – условие принятия гипотезы о том, что данная случайная величина подчиняется нормальному распределению. Этот критерий выражается следующим неравенством:

набл2 . < крит2 .

где набл2 . – статистика, а крит2 . – величина, зависящая от уровня значимости и

числа степеней свободы . Значения крит2 . табулированы.

Если данное неравенство выполняется, то закон теоретического распределения (в нашем случае – нормального) не противоречит опытным данным и нет оснований отвергать гипотезу 0. В противном случае нулевая гипотеза отвергается.

Постановка задачи.

Для заданной надежности определить (на основании выборочных данных и результатов выполнения лабораторной работы №2) границы доверительных интервалов для математического ожидания и среднеквадратичного отклонения случайной величины. Проверить гипотезу о нормальном распределении исследуемой случайной величины с помощью критерия Пирсона 2. Дать содержательную интерпретацию полученным результатам.

4

Исходные данные – данные и результаты из лабораторной работы №2 и лабораторной работы №1.

Полный код программы представлен в приложении А.

Выполнение работы.

Первым делом были вычислены точность доверительные интервалы для

математического ожидания при неизвестном среднеквадратичном отклонении и

заданном объёме выборки ( = 111). Доверительная надёжность

{0.95, 0.99}. По таблице найдено значение коэффициента Стьюдента ( , ).

Для первого случая 1(111, 0.95) = 1.98, для второго – 2(111, 0.99) = 2.62.

По формуле (3) была найдены значения точности 1 и 2. Результаты представлены на рис. 1:

Рисунок 1 – Вычисленные значения точности Далее, по формулам (2) и (3), учитывая данные прошлых лабораторных

работ, были найдены границы интервалов (см. рис. 2).

Рисунок 2 – Левые и правые границы найденных интервалов Таким образом, получились следующие интервалы: (91.9247; 107.8726) и

(89.3472; 110.4501). Исходя из полученных результатов, можно сделать вывод о том, что оба интервала с определённой точностью покрывают значение математического ожидания. Так как при нахождении второго интервала надёжность бралась больше, границы этого интервала расположены дальше друг от друга, нежели у первого интервала, а значит второй интервал точнее покрывает нужный параметр.

Теперь были найдены доверительные интервалы для СКО при тех же и= 111 (см. лаб. работу №2). Значения были взяты из таблицы и равны:

5

1(111, 0.95) = 0.139 и 2(111, 0.99) = 0.190. С этими значениями, по формулам (4) и (5) были вычислены границы доверительного интервала для среднеквадратичного отклонения. Результаты представлены на рис. 3:

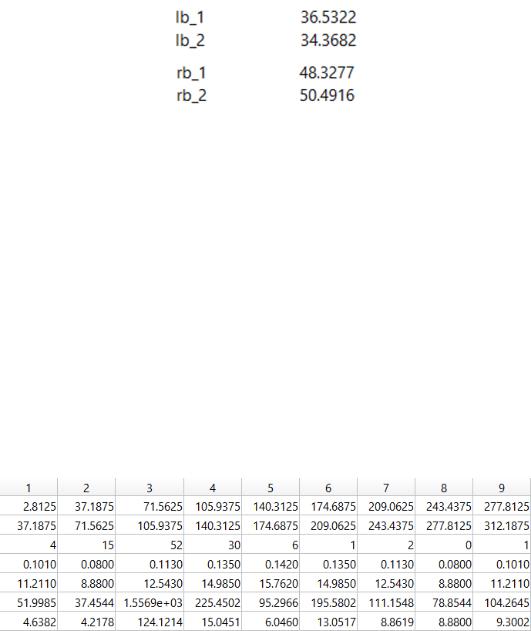
Рисунок 3 – Левые и правые границы найденных интервалов Таким образом, получились следующие интервалы: (36.5322; 48.3277) и

(34.3682; 50.4916). Исходя из полученных результатов, можно сделать вывод о том, что оба интервала с определённой точностью покрывают значение среднеквадратичного отклонения. Так как при нахождении второго интервала надёжность бралась больше, границы этого интервала расположены дальше друг от друга, нежели у первого интервала, а значит второй интервал точнее покрывает нужный параметр.

Далее была выдвинута гипотеза о том, что исследуемая случайная величина подчиняется закону нормального распределения. Результаты промежуточных вычислений представлены на рис. 4:

Рисунок 4 – Процесс нахождения набл2 .

Рассмотрим рис. 4. На первой строчке расположены порядковые номера интервалов. Далее, на второй строчке, расположились левые границы интервалов, а на третьей строчке – правые границы. На четвёртой строчке идут значения эмпирических частот . Далее, вычисленные по формуле (6),

расположились значения точечных вероятностей . После этого, по формуле (7),

были высчитаны значения выравнивающих частот ′ и записаны в шестую

6

строку. На седьмой строке расположились значения квадратов разностей и

′.

В конце концов, по формуле (8), была высчитана набл2 .. Она оказалась равна 194.1623. Число степеней свободы, по формуле (10), равно 6. Из условий задачи, = 0.05. По таблице находим значение крит2 .(0.05, 6) = 12.6. Проверяем, выполняется ли критерий Пирсона:

194.1623 < 12.6

Видно, что неравенство неверное, а значит имеются основания отвергнуть изначальную гипотезу о нормальности распределения генеральной совокупности.

Выводы.

В ходе выполнения лабораторной работы были найдены доверительные интервалы для математического ожидания и среднеквадратичного отклонения с различными значениями заданной надёжности. В итоге, стало видно, что чем больше надёжность, тем выше точность и больше интервал, а значит, он точнее покрывает нужный параметр.

Также была выдвинута гипотеза о нормальности заданного распределения.

Так как критерий Пирсона не выполняется, был сделан вывод о том, что эта гипотеза должна быть отвергнута.

7

ПРИЛОЖЕНИЕ А

ПРОГРАММНЫЙ КОД (ЯЗЫК ПРОГРАММИРОВАНИЯ – MATLAB)

%% Третья работа % Пункт 1

GAMMA_1 = 0.95; GAMMA_2 = 0.99; t_gamma_1 = 1.98; t_gamma_2 = 2.62;

prod_1 = t_gamma_1 * COR_SKO; delta_1 = prod_1 / sqrt(N);

prod_2 = t_gamma_2 * COR_SKO; delta_2 = prod_2 / sqrt(N);

left_border_1 = SEL_AVR - delta_1; right_border_1 = SEL_AVR + delta_1;

left_border_2 = SEL_AVR - delta_2; right_border_2 = SEL_AVR + delta_2; % Пункт 2

q_1 = 0.139; q_2 = 0.190;

lb_1 = COR_SKO * (1 - q_1); rb_1 = COR_SKO * (1 + q_1);

lb_2 = COR_SKO * (1 - q_2); rb_2 = COR_SKO * (1 + q_2); % Пункт 3

alpha = 0.05;

SOLUTION = randi(1, 7, n);

laplas = [-0.500, -0.399, -0.319, -0.206, -0.071, 0.071, 0.206, 0.319, 0.399, 0.5];

hi_sqr = 0; for i = 1 : n

SOLUTION(1, i) = GAPS_ROW(1, i); SOLUTION(2, i) = GAPS_ROW(2, i); SOLUTION(3, i) = GAPS_ROW(3, i); SOLUTION(4, i) = laplas(i + 1) - laplas(i); SOLUTION(5, i) = N * SOLUTION(4, i);

subtr = SOLUTION(3, i) - SOLUTION(5, i); SOLUTION(6, i) = subtr ^ 2;

SOLUTION(7, i) = SOLUTION(6, i) / SOLUTION(5, i); hi_sqr = hi_sqr + SOLUTION(7, i);

end;

df = n - 3; hi_sqr_v = 12.6;

8