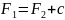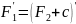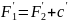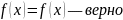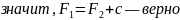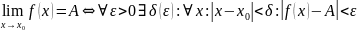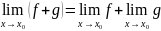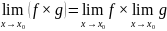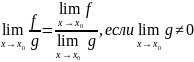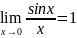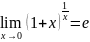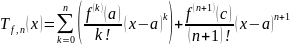Семестр 1 / Ответы на экзаменационные вопросы
.docxНепрерывность функции в точке — определение. Непрерывность функции в области — определение. Является ли <функция> непрерывной на своей области определения? Ответ обоснуйте.

 или
или
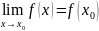
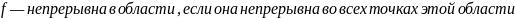 .
.Решение через
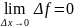 ;
;
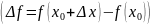 Пример
для
Пример
для
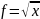 :
:
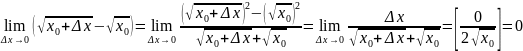
Непрерывность функции в точке — определение. Теорема об арифметических действиях над непрерывными функциями. Является ли <функция> непрерывной на своей области определения? Ответ обоснуйте.
См. (1)
Если:

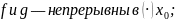 Тогда:
Тогда:
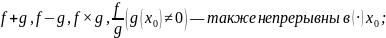
См. (1)
Предел функции в точке x0 ∈ R — определение. Теорема о пределах суммы, произведения и частного функций.
Предел функции на бесконечности — определение. Теорема о пределах суммы, произведения и частного функций.
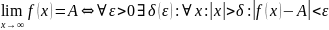
См. (3)
Предел функции в точке x0 ∈ R — определение. Теорема о пределе композиции функций.
См. (3)
Если:
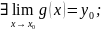
 Тогда:
Тогда:
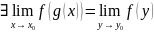
Предел функции на бесконечности — определение. Теорема о пределе композиции функций.
См. (4)
См. (5)
Предел последовательности. Привести пример последовательности, сходящейся к конечному пределу.
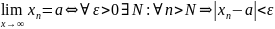
Пример:
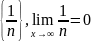
Предел последовательности. Привести пример последовательности, сходящейся к бесконечному пределу.
См. (7)
Пример:
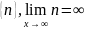
Предел последовательности. Привести пример последовательности, не имеющей предела.
См. (7)
Пример:
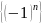
Последовательность, сходящаяся в себе — определение. Является ли <последовательность> сходящейся в себе? Ответ обоснуйте.
Последовательность, для которой выполняется условие Коши:
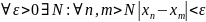
Если последовательность имеет конечный предел, то для неё выполняется условие Коши.
Первый замечательный предел.
Второй замечательный предел.
Теорема Больцано (о корне). Удовлетворяет ли <функция> на указанном промежутке т. Больцано? Ответ обоснуйте.
Если:
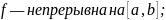
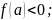
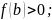 или
или
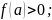
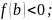 Тогда:
Тогда:
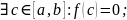
Доказать непрерывность, показать, что
 и
и
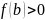 или наоборот.
или наоборот.
Теорема Вейерштрасса (о достижении наибольшего и наименьшего значений). Удовлетворяет ли <функция> на указанном промежутке т. Вейерштрасса? Ответ обоснуйте.
Если: Тогда:
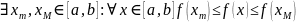
Доказать непрерывность функции.
Дифференцируемая функция — определение. Теорема о производной суммы, произведения и частного функций. Является ли <функция> дифференцируемой в указанной точке? Ответ обоснуйте.
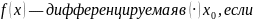
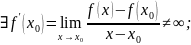
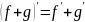
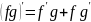
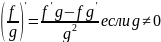
Посчитать предел из 1-го подпункта.
Дифференцируемая функция — определение. Теорема о производной композиции функций. Является ли <функция> дифференцируемой в указанной точке? Ответ обоснуйте.
См. (15)
Если:
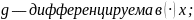
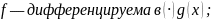 Тогда:
Тогда:
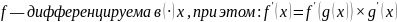
См. (15)
Монотонность функции. Связь (строгой) монотонности и первой производной. Является ли <функция> (строго) монотонной? Ответ обоснуйте.
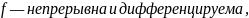
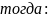
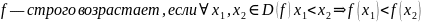
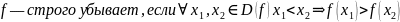
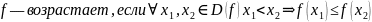

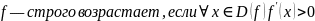
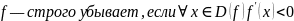

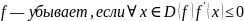
Найти производную и узнать, когда она положительна, отрицательна и равна нулю.
Теорема Ролля.
Если:

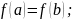 Тогда:
Тогда:
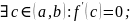
Теорема Лагранжа.
Если: Тогда:
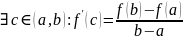
Теорема Коши.
Если:
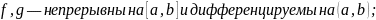
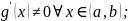 Тогда:
Тогда:

Правило Лопиталя. Из какой теоремы следует правило Лопиталя?
Если:
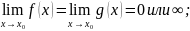 Тогда:
Тогда:
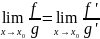
Следует из теоремы Коши.
Формула Тейлора с остатком в форме Пеано. Выписать формулу Тейлора для <функции>.
Формула Тейлора с остатком в форме Лагранжа. Выписать формулу Тейлора для <функции>.
В
 ыпуклость
функции.
Связь (строгой) выпуклости
и второй производной.
Является
ли<функция>
(строго)
выпуклой?
ыпуклость
функции.
Связь (строгой) выпуклости
и второй производной.
Является
ли<функция>
(строго)
выпуклой?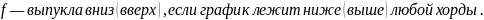

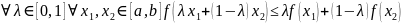
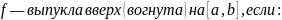
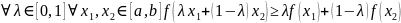
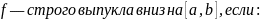
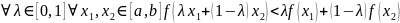
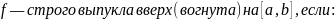
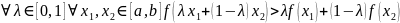
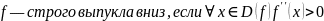
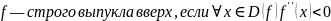
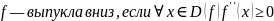
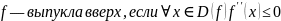
Найти 2-ю производную и узнать, когда она больше, меньше и равна нулю.
Первообразная — определение. Теорема о классе первообразных данной функции. Является ли одна из <функций> первообразной для другой? Ответ обоснуйте.
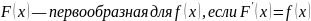
Если:
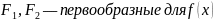 Тогда:
Тогда:

Найти производную первой функции. Если ответ получился равен второй функции, значит первая — первообразная для второй.
Вопросы 2 этапа
Функция. Определение, инъективность, сюръективность, биективность. Композиция функций. Обратная функция.
Определение функции
Функция — закон, по которому каждому элементу заданного множества
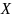 ставится в соответствие элемент
множества
ставится в соответствие элемент
множества
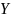 .
.
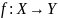
Инъективность
— инъективна, если

Сюръективность
— сюръективна, если
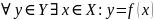
Биективность
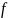 —
биективна, если она
инъективна и сюръективна
—
биективна, если она
инъективна и сюръективна
Композиция функций
Пусть
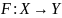 и
и
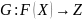 —
две функции (
—
две функции (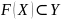 ).
Тогда их композицией называется
функция
).
Тогда их композицией называется
функция
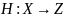 ,
что
,
что

Обратная функция
— биективна, тогда
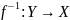 — обратная функция
— обратная функция
Непрерывность функции в точке и в области. Теорема об арифметических действиях над непрерывными функциями.
Непрерывность функции в точке
или
Непрерывность функции в области
.
Теорема об арифметических действиях над непрерывными функциями
Если: Тогда: Доказательство: по определению непрерывности
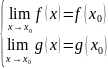 по
теореме о пределах суммы, произведения
и частного функций:
по
теореме о пределах суммы, произведения
и частного функций:
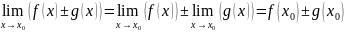
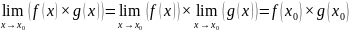
 тогда
по определению эти функции непрерывны
в точке
тогда
по определению эти функции непрерывны
в точке
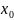
Непрерывность функции в точке и в области. Теорема о композиции непрерывных функций.
Если:
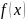 — непрерывна в
— непрерывна в
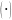
 — непрерывна в
— непрерывна в
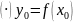 Тогда:
Тогда:
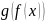 — непрерывна в
— непрерывна в
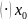 Доказательство:
Доказательство:
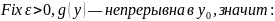

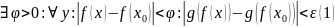
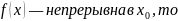
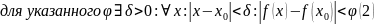
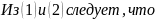
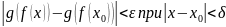
Предел функции. Теорема о пределах суммы, произведения и частного функций.
Предел функции
Теорема о пределах суммы, произведения и частного функций
Доказательство: Пусть
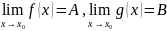 Тогда
по теореме
о связи функции, её предела и бесконечно
малой функции:
Тогда
по теореме
о связи функции, её предела и бесконечно
малой функции:
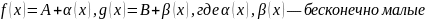 Выразим:
сумму:
Выразим:
сумму:
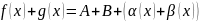 произведение:
произведение:
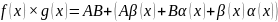 частное:
частное:
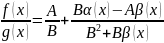 По
свойствам
бесконечно малых:
По
свойствам
бесконечно малых:
 Тогда
по теореме
о связи функции, её предела и бесконечно
малой функции:
Тогда
по теореме
о связи функции, её предела и бесконечно
малой функции:

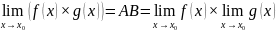
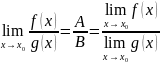
Предел функции. Теорема о пределе композиции функций.
Если:
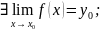
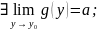 Тогда:
Тогда:
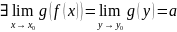 Доказательство:
Доказательство:
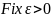
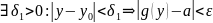
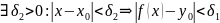
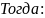
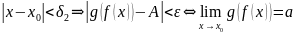
Предел последовательности.
Последовательность, сходящаяся в себе — определение. Критерий Коши.
Последовательность, сходящаяся в себе
Критерий Коши.
Если:
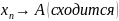 Тогда:
Тогда:
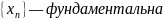 Доказательство:
Доказательство:
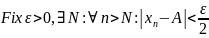
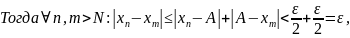
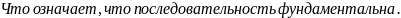
Первый замечательный предел.
Доказательство: Докажем, что односторонние пределы
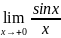 ,
,
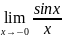 равны 1.
равны 1.
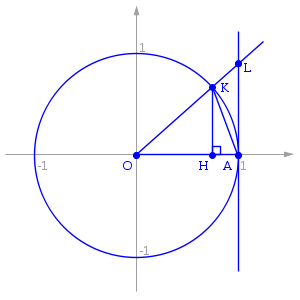
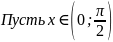 Отложим
этот угол на единичной окружности
так, чтобы его вершина совпадала с
началом координат, а одна сторона
совпадала с осью
Отложим
этот угол на единичной окружности
так, чтобы его вершина совпадала с
началом координат, а одна сторона
совпадала с осью
 .
Пусть
.
Пусть
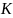 — точка пересечения второй стороны
угла с единичной окружностью, а точка
— точка пересечения второй стороны
угла с единичной окружностью, а точка
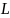 — с касательной к этой окружности в
точке
— с касательной к этой окружности в
точке
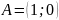 .
Точка
.
Точка
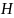 — проекция точки
на ось
.
— проекция точки
на ось
.

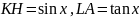
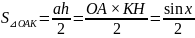
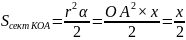
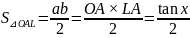 Подставляя
в (1), получаем:
Подставляя
в (1), получаем:
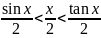
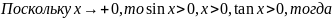
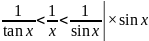
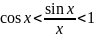 Перейдём
к пределу:
Перейдём
к пределу:
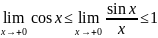
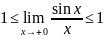
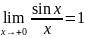 Найдём
левый односторонний предел:
Найдём
левый односторонний предел:
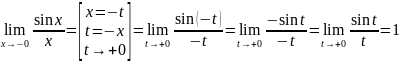 Тогда:
Тогда:
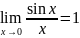
 Второй
замечательный предел.
Второй
замечательный предел. Доказательство:
Доказательство:
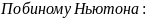
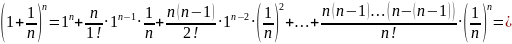
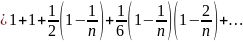
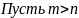
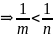

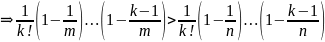
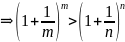
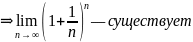
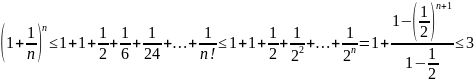
Теорема Больцано (о корне).
Если:
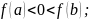 или
или
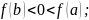 Тогда:
Доказательство:
Рассмотрим
случай с
Тогда:
Доказательство:
Рассмотрим
случай с
 (для другого случая аналогично)
(для другого случая аналогично)
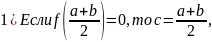
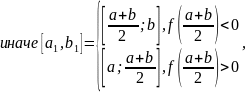
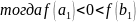

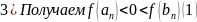

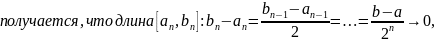
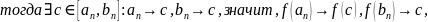
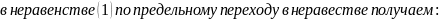
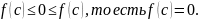
Теорема Вейерштрасса (о достижении наибольшего и наименьшего значений).
Если: Тогда: Доказательство: Рассмотрим случай для верхней границы (для нижней по аналогии)
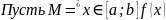
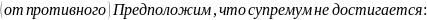
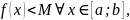
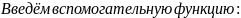
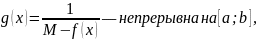

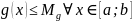
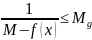
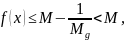
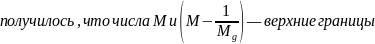
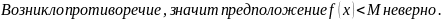
Дифференцируемая функция. Теорема о производной суммы, произведения и частного функций.
Дифференцируемая функция.
Теорема о производной суммы, произведения и частного функций.
Доказательство: сумма:
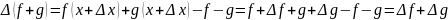
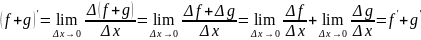 произведение:
произведение:
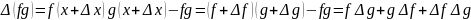
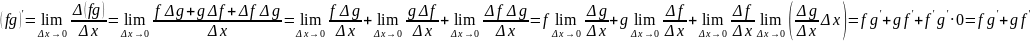 частное:
частное:
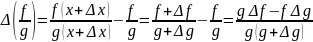
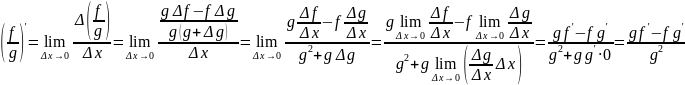
Дифференцируемая функция. Теорема о производной композиции функций.
Если: Тогда:
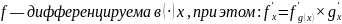 Доказательство:
Доказательство:
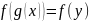
Монотонность функции.
Доказательство: случай для возрастания (для остальных по аналогии)
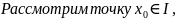
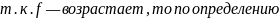
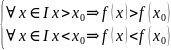
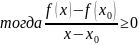
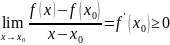
Теорема Ролля.
Если: Тогда: Доказательство:
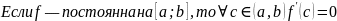

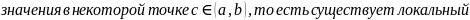
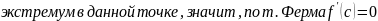
Теорема Лагранжа.
Если: Тогда: Доказательство:
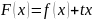
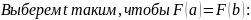
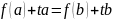

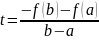

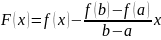

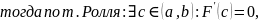
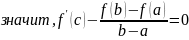
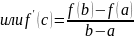
Теорема Коши.
Если: Тогда: Доказательство:
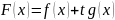

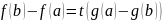

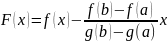
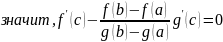
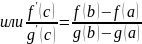
Формула Тейлора с остатком в форме Пеано.
Доказательство:
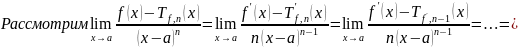
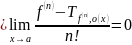
Формула Тейлора с остатком в форме Лагранжа.
Выпуклость функции.
Первообразная. Теорема о классе первообразных данной функции.
Первообразная.
Теорема о классе первообразных данной функции.
Если: Тогда: Доказательство: