АиСД_Курсовая_Отчёт_Заболотников_9373

Рис. 5. Остовное дерево графа G (состоит из красных рёбер).

Из рисунка видно, что граф может иметь не одно остовное дерево.

Например, мы могли не удалять ребро BE, а удалить ребро ED.

Полученный подграф тоже являлся бы остовным деревом нашего графа.

Чтобы дать определение минимальному остовному дереву,

определим понятие взвешенного графа. Взвешенный граф – это граф, с

каждым ребром которого связано какое-то число, или вес ребра. Сделаем из нашего графа с рис. 1 взвешенный граф (рис. 6):

Рис. 6. Взвешенный граф.

Теперь у каждого ребра есть свой вес: AB – 3, BC – 7, CE – 2, ED – 1, DA – 10, AC – 8 и BE – 5.

И теперь переходим к главному. Что такое минимальное остовное дерево? Минимальное остовное дерево взвешенного графа – это остовное дерево с наименьшим суммарным весом (суммарный вес дерева (или

11

любого взвешенного графа) – это сумма весов всех входящих в его состав рёбер). Например, минимальное остовное дерево нашего графа G с

рисунка 1 (см. рис. 7):

Рис. 7. Минимальное остовное дерево графа G (выделено красным).

Это дерево состоит из рёбер ED, EC, AB и BE. Его суммарный вес равен: 1 + 2 + 3 + 5 = 11. Поиск минимального остовного дерева связного неориентированного взвешенного графа может быть осуществлён с помощью алгоритма Крускала, что и является основной задачей данной работы.

12

2. ОПИСАНИЕ ЛГОРИТМОВ, ИСПОЛЬЗОВАВШИХСЯ ПРИ

СОЗДАНИИ ПРОГРАММЫ.

2.1.Хранение элементов графа. Обход графа в глубину.

Вначале в программу поступает граф в виде строки символов

«Р1В1Р2В2Р3В3 ... РnВn», где Рi – ребро графа, обозначаемое двумя вершинами (его началом и концом), а Вi – его вес. Задать граф можно двумя способами: либо непосредственным вводом с клавиатуры, либо чтением из файла. Стартовое меню изображено на рисунке 8:

Рис. 8. Стартовое меню программы.

Как только граф был тем или иным образом получен, его сразу же конвертируем в масив graph[ ], элеметы которого являются структурными перемеными пользовательского типа даных struct Edges, включающего в себя название ребра и его вес. После того, как граф был конвертирован в данный массив, строится матрица смежности для этого графа. Эту задачу выполняет функция bool Revision( ):

Рис. 9. Код функции bool Revision( ).

13

В свою очередь, данная функция вызывает ещё две: FillMatrix( ) и

DFS( ), которые: первая заполняет матрицу смежности нулями и единицами (на пересечении тех вершин, которые являются концами очередного ребра), а вторая – производит обход графа в глубину. Коды этих двух функция представлены на рисунках 10 и 11:

Рис. 10. Функция FillMatrix( ).

Рис. 11. Функция DFS( ).

Реализация алгоритма обхода графа в глубину очень проста: на вход подаются матрица смежности графа, массив непсещённых вершин, номер стартовой вершины (с которой начнётся процедура обхода) и количество вершин в графе. В качестве наальной вершины берётся вершина, которая в матрице смежности стоит под индексами (0, 0). В начале функции в массиве непосещённых вершин вершина с текущим индексом помечается как посещённая. А дальше мы просматриваем всю текущую строку и смотрим: если в элементе с текущим индексами стоит единица (то есть существует соответствующее ребро) и текущая вершина ещё не посещена,

то рекурсивно вызываем функцию DFS( ) ещё раз. Процедура

14

продолжается, пока есть куда идти. Если в итоге получается, что алгоритм завершил свою работу, а в мссиве непосещённых вершин какие-то вершины остались непосещёнными, значит, эти вершины содержатся в другой компоненте связности и наш граф не является связным. А значит, и

минимальный остов в нём искать смысла нет.

Все функции вместе – Revision( ), FillMatrix( ) и DFS( ) – нужны для того, чтобы проверить исходный граф на связность. Ведь если граф несвязный, то остовного дерева для него не существует.

2.2.Сортировка элементов графа.

Входе программы дважды приходится сортировать данные. В

первый раз – когда сортируются рёбра графа по их весам, а второй – когда рёбра найденного остовного дерева сортируются по лексикографическому порядку. Для обоих случаев в данной программе используется сортировка слиянием – Merge Sort. Данный вид сортировки был выбран потому, что он здесь наиболее эффективен. Время его работы – O(n*log(n)). Алгоритм сортировки реализован с помощью двух функций, в следующем виде (см.

рис. 12 и 13):

Рис. 12. Функция Merge( ).

15

Рис. 13. Функция Sort( ).

Обе функции – Merge( ) и Sort( ) – выполняют одну сортировку слиянием.

2.3. Система непересекающихся множеств.

Непосредственно нахождение остовного дерева исходного графа происходит с помощью построения системы непересекающихся множеств

(здесь и далее – СНМ). СНМ – это структура данных, которая позволяет администрировать множество элементов, разбитое на непересекающиеся подмножества. При этом каждому подмножеству назначается его представитель – элемент этого подмножества. Суть агоритма построения минимального остова с помощью СНМ следующая: берётся отсортированный по весам набор рёбер исходного графа. Далее используется ранее созданный массив вершин top_list[ ], элементами которого являются переменные пользовательского типа struct Tops.

Каждый элемент этого массива хранит в себе саму вершину (букву) и её номер. Изначально все вершины рассматриваются как отдельные непересекающиеся множества. А дальше начинается сам алгоритм. Берём очередное ребро из массива рёбер graph[ ] и проверяем: если данное ребро

16

объединяет две вершины из разных множеств, записываем это ребро в результирующий сет, а объединённые вершины соединяем в одно множество. Если так окажется, что очередное ребро соединяет две вершины из одного множества, значит, у нас образовался цикл.

Следовательно, это ребро нам не подойдёт и мы его пропускаем. Действие алгоритма заканчиватся тогда, когда все вершины окажутся объединёнными в одно множество. Код реализации данного алгоритма показан на рисунке 14:

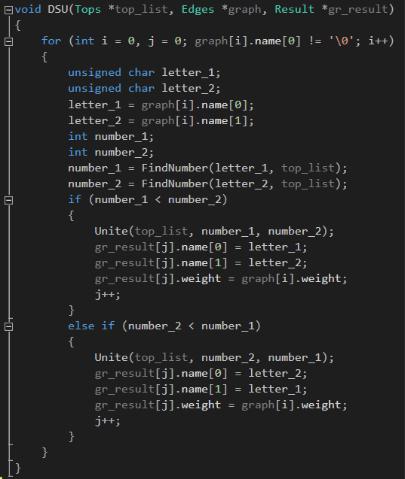
Рис. 14. Функция DSU( ).

Функция, реалзующая алгоритм, называется DSU( ), она записывает

вмассив gr_result[ ] рёбра строящегося минимального остова.

Минимальность получившегося остова гарантируется тем, что массив рёбер исходного графа был упорядочен по неубыванию по весам рёбер. То есть из всех предложенных оставшихся рёбер мы выбираем всегда

наименьшее.

17

В итоге мы получаем список рёбер, входящих в минимальный остов нашего графа. Далее необходимо было отсортировать этот список в лексикографическом порядке. Для того, чтобы это сделать, снова была выбрана сортировка слияинем.

После того, как рёбра отсортированы, результирующий сет надо вывести на экран вместе с суммарным весом. За это отвечает данный кусок кода, представленный на рисунке 15:

Рис. 15. Вывод рёбер остовного дерева.

На этом программа заканчивает выполнение основного алгоритма и ждёт, пока пользователь не нажмёт какую-нибудь клавишу, чтобы закрыться. Примеры запуска программы показаны в приложении А.

18

ЗАКЛЮЧЕНИЕ

В ходе написания программы были реализованы алгоритмы: хранения графов (матрица смежности), обхода графа в глубину, сортировки (сортировка слиянием) и системы непересекающихся множеств. Программа соответствует требованиям и успешно выполняет поставленную задачу – нахождение минимального остовного дерева в графе. Наглядно с результатами работы программы можно ознакомиться в приложении А.

19

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.Система непересекающихся множеств.

URL: https://habr.com/ru/post/104772/

2.Обход графа в глубину.

URL: https://kvodo.ru/dfs.html

3.Теоретический материал по графам.

С. К. Ландо, «Графы и топология». Издательство: 24 февраля 2018

года.

20