
Определенные интегралы / Opr1
.pdf
Лекция № 1. Определённый интеграл
Задачи, приводящие к понятию определённого интеграла
1. Задача о площади криволинейной трапеции.
Пусть на отрезке [a ; b] задана функция f ( x) ³ 0 . Требуется найти площадь
S фигуры, образованной осью Ox, прямыми: |
x = a ; x = b и графиком функции |
y = f ( x) (криволинейная трапеция). |
y = f ( x) |
у |
|
|
|
хi-1 ξi |
|
|
|
x |
|
|
|
|
О |
а |
xi |
b |
|
|
|
|
||
Разобьём отрезок [a ; b] на п частей: |
a = x0 < x1 < ... < xn |
= b . На каждом |
||||||||
участке разбиения |
[xi−1 ; xi ] (i =1, ..., n) |
выберем |
точку |
ξi [xi−1 ; xi ] |
и |
|||||
составим сумму |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
Sn = ∑ f (ξi ) |
xi , |
где |
xi = xi |
− xi −1 . |
|
|
(1) |
|
Тогда S ≈ Sn |
|
i=1 |
|
|
|
|
|
|
|
|
, так |
как Sп |
геометрически |
представляет |
собой |
площадь |
|||||
ступенчатой фигуры. Если теперь перейти к пределу в формуле (1), |
когда |
все |
||||||||
xi →0 n →∞, то |
получим |
значение |
площади криволинейной |
трапеции, |
||||||
т.е.
n
S = lim ∑ f (ξi ) xi .
Δxi →0 i =1
2. Задача о массе тела.
Задан линейный неоднородный стержень с плотностью γ ( x) , лежащий в пределах [a ; b] . Требуется определить его массу М. Как и ранее, разобьём отрезок
[a ; b] на части. Так как в пределах xi |
плотность γ ( x) |
изменяется |
мало, |
то |
||
mi ≈ γ (ξi ) |
xi , а масса стержня |
|
|
|
|
|
|
n |
) xi . |
|
|
|
|
|
M ≈ M n = ∑γ (ξi |
|
|
|
||
|
i =1 |
|
|
|
|
|
Точное |
значение массы получим, |
если |
перейти |
к пределу, |
когда |
все |
xi →0 n →∞ |
|
|
|
|
|
|
n
M = lim ∑γ (ξi ) xi .
Δxi →0 i =1

Определение определённого интеграла
Пусть на отрезке [a ; b] задана функция f ( x) . Разделим отрезок
части произвольным образом точками: |
a = x0 |
< x1 < ... < xn = b . На |
|
полученных отрезков разбиения [xi−1 ; xi ] (i = 1, ..., n) |
произвольно |
||
точку ξi [ xi − 1 ; xi ] и составим сумму |
|
|
|
n |
|
xi = xi |
− xi−1 , |
I n = ∑ f (ξ i ) |
xi , где |
||
i =1
[a ; b] на каждом из выберем
(2)
называемую интегральной суммой функции f ( x) на отрезке [a ; b] . Определение 1. Если предел интегральной суммы (2) не зависит от способа
разбиения отрезка [a ; b] и выбора точек ξi , то он называется определённым
интегралом от функции f ( x) |
на отрезке [a ; b] и обозначается |
|
|||
|
In = |
|
n |
b |
|
lim |
lim |
∑ f (ξi ) xi = |
∫ f ( x)dx , |
(3) |
|
Δxi →0 |
Δxi →0 |
i=1 |
a |
|
|
где а − нижний, b − верхний пределы интегрирования. |
|
|
|||
Определение 2. Если для функции f ( x) на отрезке [a ; b] существует предел |
|||||
(3), то функция f ( x) называется интегрируемой на [a ; b] . |
|
||||
При каких условиях существует предел (3)? |
|
f ( x) |
|||
Теорема 1 (теорема существования определённого интеграла). Если |
|||||
непрерывна на отрезке [a ; b] , то она интегрируема на [a ; b] . |
|
||||
Замечание. Среди разрывных |
функций на [a ; b] |
есть как интегрируемые |
|||
(ограниченные монотонные), так и неинтегрируемые. Например, неинтегрируемой является функция Дирихле
1, x − рациональное;
D (x) =
0, x − иррациональное.
Действительно, если в качестве точек ξi выбрать рациональные точки и рассмотреть функцию Дирихле на отрезке [0 ; 1] , то из формулы (3) интегральная сумма будет равна 1, а если в качестве точек ξi выбрать только иррациональные точки, то 0. Таким образом, предел (3) не существует.
Теперь выясним геометрический смысл определённого интеграла:
Из ранее рассмотренной задачи при f ( x) ³ 0 − это площадь криволинейной трапеции. При f ( x) < 0 − это тоже площадь, но со знаком минус. Поэтому определённый интеграл – это алгебраическая площадь криволинейной трапеции.
у
Å
х
−

Физический смысл определённого интеграла.
Из ранее рассмотренной задачи масса стержня с линейной плотностью γ ( x)
b
определяется как M = ∫γ ( x )dx .
a
Рассуждая подобным образом, получаем, что если F ( x) − сила, действующая вдоль прямолинейного отрезка [a ; b] , то работа этой силы
b
A = ∫F ( x)dx .
a
Основные свойства определённого интеграла
b
1. Если M = const, то ∫Mdx = M (b −a).
a
n
Действительно, I n = M ∑ xi = M (b − a ) .
i =1
2.
[a ; b]
Свойство линейности. Если функции |
f ( x) и g ( x) интегрируемые на |
|
и А, В − const, |
то |
|
b |
b |
b |
∫(Af ( x ) + Bg ( x ) )dx = A ∫ f ( x )dx + B ∫ g ( x )dx . |
||
a |
a |
a |
Это свойство вытекает из определения определённого интеграла. |
|
|||||||||
3. |
При перестановке местами пределов интегрирования определенный |
|||||||||
|
|
|
|
b |
|
a |
|
|
|
|
интеграл меняет свой знак |
∫ f ( x)dx = −∫ f ( x)dx . |
|
|
|
|
|||||
|
|
|
|
a |
|
b |
|
|
|
|
Это |
свойство |
следует |
из |
того, что |
в интегральной |
сумме |
все |
разности |
||
xi = xi |
− xi −1 меняют знак. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a |
|
|
|
4. |
Если пределы интегрирования одинаковы, то |
∫ f ( x)dx = 0 . |
|
|||||||
|
|
|
|
|
|
|
a |
|
|
|
Действительно, так как все разности |
xi = xi − xi −1 = 0 . |
|
|
|||||||
5. |
Свойство аддитивности. |
Если a < c < b , то |
|
|
|
|
||||
|
|
|
b |
|
c |
b |
|
|
|
|
|
|
|
∫ f ( x)dx = ∫ f ( x)dx + ∫ f ( x)dx . |
|
|
|
||||
|
|
|
a |
|
а |
c |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
6. |
Если f ( x ) ³ 0 |
∫ f ( x ) d x ³ 0 . |
|
|
|
|
||||
|
|
|
|
|
a |
|
|
|
|
|
Это |
свойство |
очевидно, |
так как |
в интегральной |
сумме |
все |
слагаемые |
|||
f (ξ i ) |
|
x i больше или равны нулю. |
|
|
|
|
|
|||
7. |
Если на отрезке [a ; b] функции f ( x) и g ( x) |
удовлетворяют неравенству |
||||||||
f ( x) ³ g ( x) , то
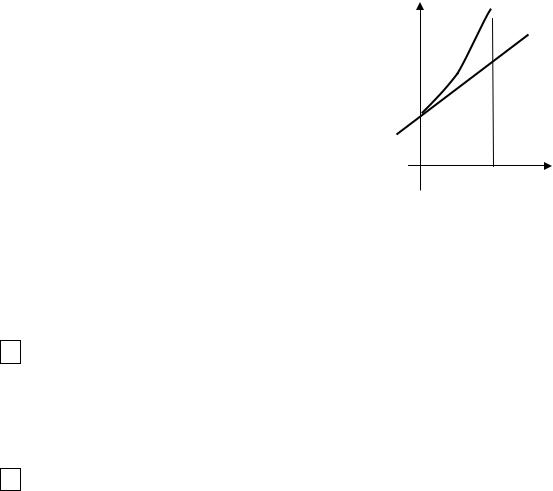
|
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∫ f ( x ) dx ³ ∫ g ( x ) d x . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Действительно, если рассмотреть разность интегралов, то с учетом свойств 2 и |
||||||||||||||||||||||
6, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∫ f (x)dx - ∫ g(x)dx = ∫( f (x) - g(x)) dx ³ 0, |
|
|
|||||||||||||||||||
|
a |
|
|
a |
a |
|
|
|
|
|
|
|
|
|
f (x) = 3x |
|
||||||
откуда и следует доказываемое неравенство. |
|
|
|
|
|
|
у |
|
|
|
||||||||||||
Данное свойство применяется для срав- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
нения определенных интегралов без их непо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
средственного вычисления. |
f (x) = 3x и |
|
|
|
|
|
|
|
g(x) = x +1 |
|
|
|||||||||||
Пример 1. Пусть функции |
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
g(x) = x +1 заданы на отрезке |
[0 ; 1] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнить интегралы |
∫ 3 x d x и |
∫ ( x + 1) d x . |
|
|
О |
1 |
|
|
х |
|
||||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построив графики данных функций, видим, что на отрезке [0 ; 1] . |
||||||||||||||||||||||
f (x) = 3x ³ g(x) = x +1, поэтому по свойству 7 получим |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∫ 3 x d x ³ ∫ ( x + 1) d x . |
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8. |
∫ f ( x ) d x |
£ ∫ |
|
f ( x ) |
|
d x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проинтегрировав |
очевидное неравенство |
- |
|
f (x) |
|
£ f (x) £ |
|
f (x) |
|
|
и, |
учитывая |
||||||||||
|
|
|
|
|||||||||||||||||||
свойство 7, приходим к данному свойству. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9. Оценка определённого интеграла. Если т и М - наименьшее и наибольшее |
||||||||||||||||||||||
значения непрерывной функции f ( x) на [a ; b] , то |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(b − a) ≤ ∫ f ( x)dx ≤ M (b − a) . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрируя неравенство m ≤ f ( x) ≤ M |
с учетом свойств 1 и 7, |
получаем |
||||||||||||||||||||
данное свойство.
Свойство 9 применяется для оценки величины определенного интеграла без его непосредственного вычисления.
|
|
|
3 |
|
Пример 2. Оценить величину интеграла |
∫ ( x 2 - 2 x + 3)dx . |
|
||
|
|
|
0 |
|
Для |
подынтегральной |
функции f ( x) |
найдем наименьшее |
и наибольшее |
значения. |
Приравнивая |
ее производную |
нулю 2x − 2 = 0 , |
находим точку |
x = 1 [0 ; 3] , подозрительную на экстремум. Вычисляя последовательно
f (0) = 02 - 2 ×0 + 3 = 3;
f (1) = 12 - 2 ×1 + 3 = 2 ; f (3) = 32 - 2 ×3 + 3 = 6,
находим |
наименьшее т = 2 и |
наибольшее |
значения М = 6 подынтегральной |
|||||||
функции |
f ( x) на рассматриваемом отрезке интегрирования [0 ; 3]. |
|||||||||
|
Тогда, учитывая, что b − a = 3 , |
|
окончательно получим |
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
6 ≤ ∫ ( x 2 − 2 x + 3) d x ≤ 1 8 . |
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
f ( x) непрерывна |
на [a ; b] , то |
||||
|
10. |
Теорема о среднем. Если |
функция |
|||||||
существует такая точка ξ [a ; b] , для которой выполняется равенство |
||||||||||
|
|
|
|
|
|
1 |
b |
|
|
|
|
|
|
f (ξ ) = |
|
∫ f ( x)dx . |
|
||||
|
|
|
b − a |
|
||||||
|
|
|
|
|
a |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Из свойства 9 получаем неравенство |
|
|
|
||||||
|
|
|
|
1 |
|
|
b |
|
|
|
|
|
|
m ≤ |
|
|
∫ f ( x)dx ≤ M . |
|
|||
|
|
|
b − a |
|
|
|||||
|
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Так |
как f ( x) непрерывна |
на |
|
[a ; b] , |
то она принимает |
все значения, |
|||
заключенные между т и М, в том числе и f (ξ ) . Из этого и следует данное свойство.
Значение функции f (ξ ) иногда называют средним интегральным значением функции f ( x) на отрезке [a ; b] .
