Добавил:

Ares_0 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

Высшая математика

Файл:

Не определенные интегралы / Integral1

.pdf

Скачиваний:

Добавлен:

12.06.2023

Размер:

520.54 Кб

Скачать

☆

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Неопределённый интеграл

F (x)

f (x)

Ранее для заданной функции

мы находили производную

F (x)

Здесь мы рассмотрим обратную задачу: производная

нам известна и

f (x) F (x)

требуется найти функцию

F (x)

С точки зрения механики – по известной скорости требуется определить закон

движения материальной точки.

Определение 1.

Функция

F (x)

называется

первообразной

на

некотором

промежутке

[a ;

для функции

f (x)

если

F (x) f (x)

для всех

х из

этого

промежутка.

Пример 1.

Если

f (x) cos x ,

то

x R получаем

F (x) sin x , так как

F (x) cos x

. Кроме того, замечаем, что первообразными будут являться также

функции

F (x) sin x 3;

F (x) sin x 0,5

и т.д.

Таким образом,

первообразные отличаются на

константу.

Теорема.	Если функции
[a ; b]	выполняется	F	(x)
	выполняется	1

Доказательство.

F1 (x)F2 (x)

и	F
	2

C ,

(x)

где

первообразные на

C const .

[a ;

то

Обозначим

Лагранжа:	(х

Ф(х) Ф(а)

Ф(х) ) (а)

С .



F1(x)( )(

F (x)
2
х а) ;	a

применимx . Так

как

этой Ф (х)

функции0 x [

теорему

a; b], то

Замечание 1. Если первообразную определить на некотором множестве, а не промежутке, то данная теорема, вообще говоря, неверна, что видно из примера:

	F (x)	1	;
Две функции	F (x)		;
Две функции	1	x
	1

образными для функции f (x)			1
образными для функции f (x)			2
			x

		1	1	, x 0
	x
F (x)
				являются перво-
2		1

			1	; x 0


	x

x ( ; 0) (0 ; ) . Однако, их разность

F (x) F (x)
1	2

	1	,	x 0	const .
				const .
1		,	x 0

Определение 2. Множество всех первообразных на некотором промежутке называется неопределённым интегралом от функции f (x) и обозначается

f (x)dx F (x) C .

Функция	f (x)	называется подынтегральной, а выражение	f (x)dx

подынтегральным. Операция нахождения неопределённого интеграла

интегрированием функции	f (x)	.

Основные свойства неопределённого интеграла

называется

f (x)dx

Действительно,

f (x)dx

d F (x) C F (x)dx f (x)dx

d F (x)dx F

(x) C

Действительно,

dF (x)

F (x)dx

f (x)dx F (x) C

Свойство

линейности:

Af (x) Bg(x) dx A

f (x)dx B

g(x)dx

B const

, где

Для доказательства продифференцируем обе части этого равенства:

Af (x) Bg(x) dx

Af (x)

для левой части

получаем

f (x)dx

g(x)dx

Af (x)

Bg(x)

для правой:

f (ax b)dx

F (ax b) C

где a , b – const .

Доказывается аналогично дифференцированием.

Таблица неопределённых интегралов

Bg(x)

;

Непосредственным дифференцированием можно проверить следующие формулы:

1.
2.
3.
4.

			x	k 1
k	dx		x			C	(k 1);
x	dx					C	(k 1);
			k	1
dx		ln x				C ;
x		ln x				C ;
x
			a		x
x	dx		a			C ;
a	dx		ln a			C ;
			ln a
exdx ex						C ;

5.	sin xdx cos x C ;
6.
	cos xdx sin x C ;
		dx			tgx C ;
7.		cos	2
				x

		dx			ctg x C ;
8.
		sin2		x

9.
	tg xdx
10.	ctg xdx

ln cos x C

ln sin x

;

C ;

12.

a x

C ;

a x

13.

arcsin

C ;

a2 x2

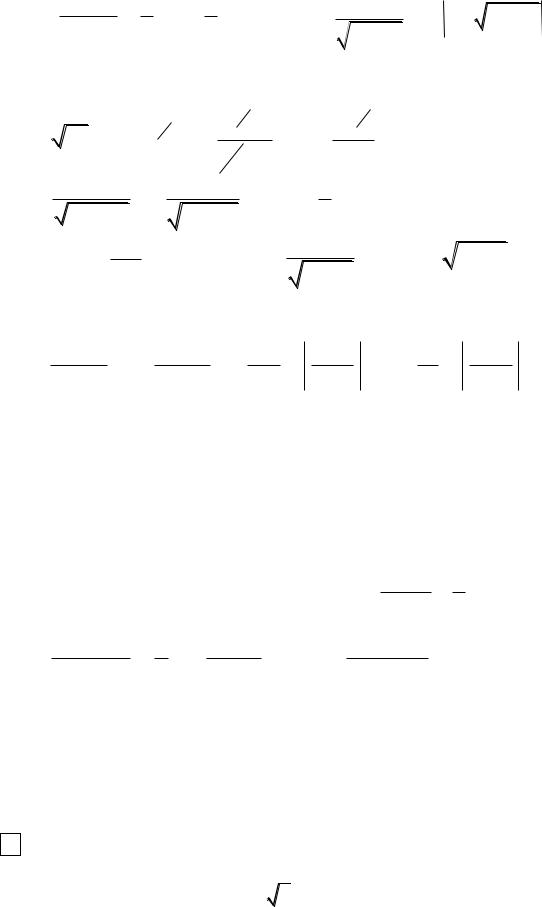
11.

dx			1	arctg	x	C ;
2	x	2	a		a

a

14.

dx		ln x	2	a	2	C ;
x	a	ln x	x	a		C ;
x	a
2		2

С помощью этой таблицы можно находить некоторые интегралы. Пример 2. Найти интегралы:

а)

б)

в)

д)

е)

C ;

arcsin

C ;

16 x

г)

5 dx

C ;

x 9

ln | x

x 9

| C ;

ln 5

arctg

C ;

x2 9

x2 32

6 x

x 6

C .

6 x

2 6

x 6

Замечание 2. Используя свойство 4, таблицу неопределённых интегралов можно расширить.

Пример 3. Найти интегралы:

а)

б)

г)

sin(3x 2)dx							1		cos(3x 2) C ;

							3
52 x 1dx				1	52 x 1	C				52 x 1		C ;	в)	dx		1
														2x 5		2
			2		ln 5					2 ln 5

	dx		2		1			1						1
	(4x	3)			4			4x 3			C		4(4x 3)		C

Элементарные преобразования подынтегральной

ln | 2x 5 | C ;

. функции.

Рассматриваемые методы основаны на использовании самых простых приемов: применения известных алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения многочленов на простые множители и свойств неопределенного интеграла.

1. Разбиение интеграла на несколько более простых интегралов путем

почленного деления числителя дроби на ее знаменатель.


Пример 4. Найти интеграл	(2	x 5)2	dx .
Пример 4. Найти интеграл		x	dx .
		x

После раскрытия скобок разделим почленно в подынтегральной функции числитель дроби на ее знаменатель и воспользуемся свойствами линейности и однородности неопределенного интеграла

x 5)

4x 20

x 25

4dx

20dx

25dx

4 dx 20

4x 40

x 25ln | x | C .

Замечание 3. На практике при вычислении интегралов константу С не пишут

отдельно для каждого интеграла, так как они в конечном итоге будут входить в окончательный ответ, содержащий произвольную константу, т.е. константа

интегрирования С пишется только один раз.
Пример 5. Найти интеграл			1			dx
	sin	2	x cos	2	x	dx	.
		2		2			.
							2	x cos	2
После замены в числителе 1	на сумму					sin	2		2	x	разделим почленно в
						sin				x

подынтегральной функции числитель дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла

sin

x cos

dx tg x ctg x C .

sin

cos

sin

x cos

2. Преобразование подынтегральной функции с помощью простейших

тригонометрических формул

sin

;

ctg

cos

;

cos

sin

ctg

sin cos 1;

2sin cos sin 2 ;

cos 2

cos2

sin2

Пример 6. Найти интеграл Имеем

	x	ctg	x
tg		ctg		dx.
	2		2

Пример 7.

Имеем

sin 2

cos 2

sin

cos

ctg

cos

sin

cos

2 cos x dx 2 ctg xdx 2 ln | sin x | C .

sin x

sin x cos x 2 dx.

Найти интеграл

sin x cos x

dx sin

x 2sin x cos x cos

(1 sin 2x)dx dx sin 2xdx x cos 2x C . 2

3. Преобразование подынтегральной функции с помощью свойств

показательной функции

	xn					n
						n

xn xm xn m ;			xn m ;	(xn )m xn m ;	m xn x m .
xn xm xn m ;	x	m	xn m ;	(xn )m xn m ;	m xn x m .
	x
Пример 8. Найти интеграл 5x 2 23x 2 dx .

5 x 22

3x 2 dx 5x 52

5x 8x dx

(5 8)x dx

40x dx

25 40x

C .

16 ln 40

Соседние файлы в папке Не определенные интегралы

#
12.06.2023520.54 Кб2Integral1.pdf
#
12.06.2023397.28 Кб1Integral2.pdf
#
12.06.2023100.32 Кб0Integral3.pdf
#
12.06.202394.22 Кб0Integral4.pdf