Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
«Южный федеральный университет»
Институт нанотехнологий, электроники и приборостроения
ОТЧЁТ
О ПРАКТИЧЕСКОЙ РАБОТЕ №4
Прохождение одномерного потенциального барьера
по дисциплине:
«Квантовая механика»
СОДЕРЖАНИЕ
1 Условие задачи 3
2 Решение задачи 4
Вывод 7
ПРИЛОЖЕНИЕ А 7
1 Условие задачи
Визуализировать потенциальный рельеф, как в презентации, для каждого из случаев в соответствии со своим вариантом. Построить график зависимостей коэффициента прозрачности T барьера от величины, указанной в таблице. На графике в каждом варианте должно быть построено 3 зависимости в соответствии с указанными условиями. Сделать выводы о характере зависимостей. Рассматриваемая частица – электрон, кроме случаев с зависимостью от массы. Зависимости T(a/V) строить не в виде функций, а по точкам (не менее 5).
Дан электрон, который может совершать одномерное движение вдоль оси X (рисунок 1), находясь при этом в потенциальном поле W(x), W — потенциальная энергия.
|
Рисунок 1 — Потенциальная яма |
Характер
этого поля таков, что для
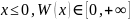 ;
для
;
для
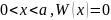 ;
для
;
для
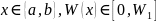 ;
для
;
для
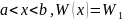 ;
для
;
для
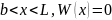 и для
и для
 .
.
Индивидуальный вариант условий приведён в таблице 1.
Таблица 1 — Индивидуальный вариант условий
Номер варианта |
l [нм] |
L [нм] |
W1 [эВ] |
W [эВ] |
Условие |
1 |
0,3; 1; 3 |
5 |
1 |
0—W1 |
T(W) |
2 Решение задачи
Чтобы решить подобного рода задачу можно воспользоваться методами теории возмущений.
Дело в том, что в квантовой механике существует небольшое число задач, которые имеют физический смысл и могут быть решены точно. Например, задача о движении свободной частицы; гармонический осциллятор; задача о движении в кулоновском потенциале. Для других задач не существует точного решения и, следовательно, не существует метода точного решения уравнения Шрёдингера.
В этом случае применяются приближенные методы, такие как: теория возмущений; квазиклассическое приближение; вариационный метод, каждый из которых основан на определенных допущениях.
В теории возмущений приближенно может решаться стационарное уравнение Шрёдингера, поэтому она также называется стационарной теорией возмущений.
Для данной задачи будет решаться для дискретного невырожденного случая, когда каждому значению энергии соответствует только одна волновая функция:
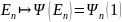
и энергия E не является непрерывной.
Пусть
есть некоторый (невозмущённый) гамильтониан
 ,
для которого известно решение стационарного
уравнения Шрёдингера. Это означает, что
существует некоторая волновая функция
,
для которого известно решение стационарного
уравнения Шрёдингера. Это означает, что
существует некоторая волновая функция
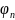 для 𝑛-о
энергетического уровня такая, что
для 𝑛-о
энергетического уровня такая, что
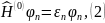
где
— пси-функция для невозмущённого
гамильтониана n-го
энергетического уровня;
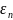 — собственное значение энергии для
n-го энергетического
уровня.
— собственное значение энергии для
n-го энергетического
уровня.
Введём
ещё одно допущение. Пусть существует
такой (возмущённый) гамильтониан
 ,
состоящий из гамильтониана
и добавки
,
состоящий из гамильтониана
и добавки
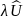 ,
которая называется возмущением:
,
которая называется возмущением:
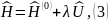
где
λ — константа связи, являющаяся
малым безразмерным параметром;
 — некоторый оператор, не зависящий от
времени.
— некоторый оператор, не зависящий от
времени.
Для возмущенного гамильтониана также существуют свои (собственные) значения пси-функций с собственными значениями энергий:
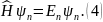
Подставив (3) в (4), получим
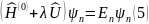
уравнение Шрёдингера в теории возмущений, которое и необходимо решить.
Вообще, метод теории возмущений удобно применять тогда, когда рассматриваемая физическая система незначительно отличается от другой физической системы, для которой известно аналитическое решение уравнения Шрёдингера.
Обозначим основные шаги общего решения уравнения (5).
Оператор является эрмитовым оператором, а собственные функции всякого эрмитова оператора образуют полный ортонормированный набор функций, то есть они могут служить базисом некоторого пространства. Это значит, что любую функцию, в том числе и волновую функцию можно представить в виде разложения по этому базису
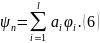
Воспользовавшись этими фактами, можно получить
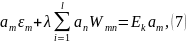
где
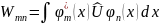 — матричный элементам возмущения. Мы
получили систему алгебраических
уравнений (с бесконечным числом строк
и столбцов) относительно коэффициентов
— матричный элементам возмущения. Мы
получили систему алгебраических
уравнений (с бесконечным числом строк
и столбцов) относительно коэффициентов
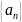 .
Эта система уравнений является точным
аналогом исходного уравнения Шрёдингера,
даже без учёта малости параметра λ.
.
Эта система уравнений является точным
аналогом исходного уравнения Шрёдингера,
даже без учёта малости параметра λ.
Чтобы решить такую систему необходимо задать ей определённый конечный размер. Например, размером три на три для некоторого k-о значения энергии Ek. Необходимо теперь воспользоваться малостью параметра λ и тем фактом, что ввиду малости возмущения ожидаемое значение энергии возмущённой задачи Ek не будет сильно отличаться от энергии невозмущённой задачи εk.
Разложим
в степенной ряд по малому параметру λ
k-ое значение энергии,
коэффициент
 .
Ограничимся разложением только до
второго порядка. Подставив найденные
выражения в исходную систему, получим:
.
Ограничимся разложением только до
второго порядка. Подставив найденные
выражения в исходную систему, получим:
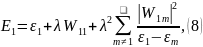
где
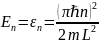 ,
,
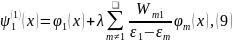
где
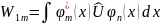 ;
;
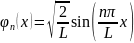 ;
n — главное квантовое
число.
;
n — главное квантовое
число.
Для m=1:

Для m≠1:
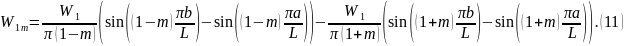
Коэффициент прозрачности T потенциального барьера определяется по формуле:

где
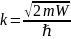 ,
,
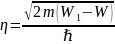 ,
,
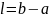 .
Чтобы вычислить значения a
и b расположим барьер,
находящийся внутри ямы, по центру её
дна, тогда
.
Чтобы вычислить значения a
и b расположим барьер,
находящийся внутри ямы, по центру её
дна, тогда
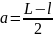 ,
,
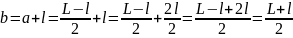 .
.
Необходимые вычисления проведём в MATLAB, а код программы приведён в приложении А.
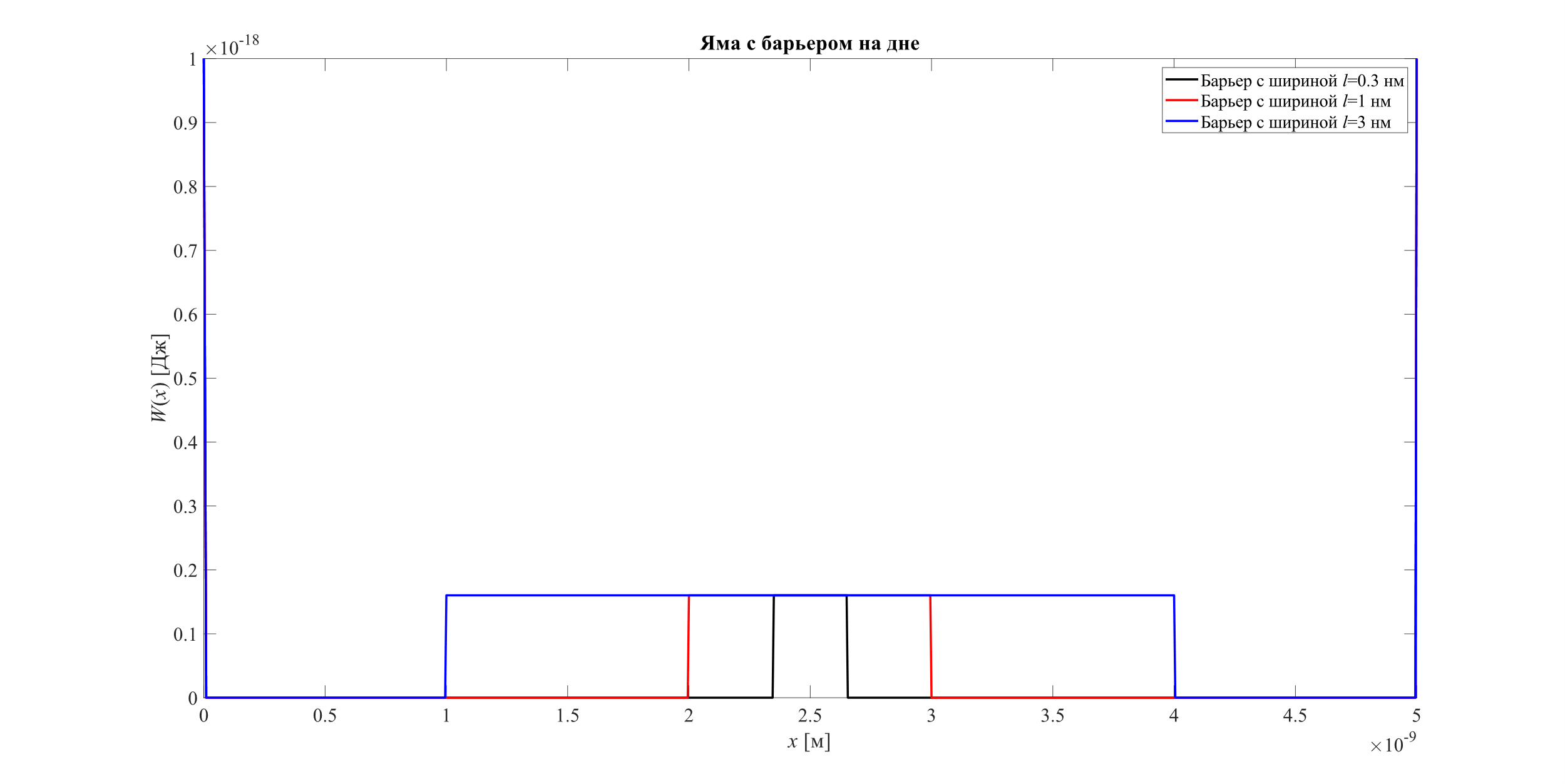
Изображение контура потенциального рельефа (барьера и ямы) приведено на рисунке 2, а изображение графика функции T(E) — на рисунке 3.
|
Рисунок 2 — Потенциальная рельеф |
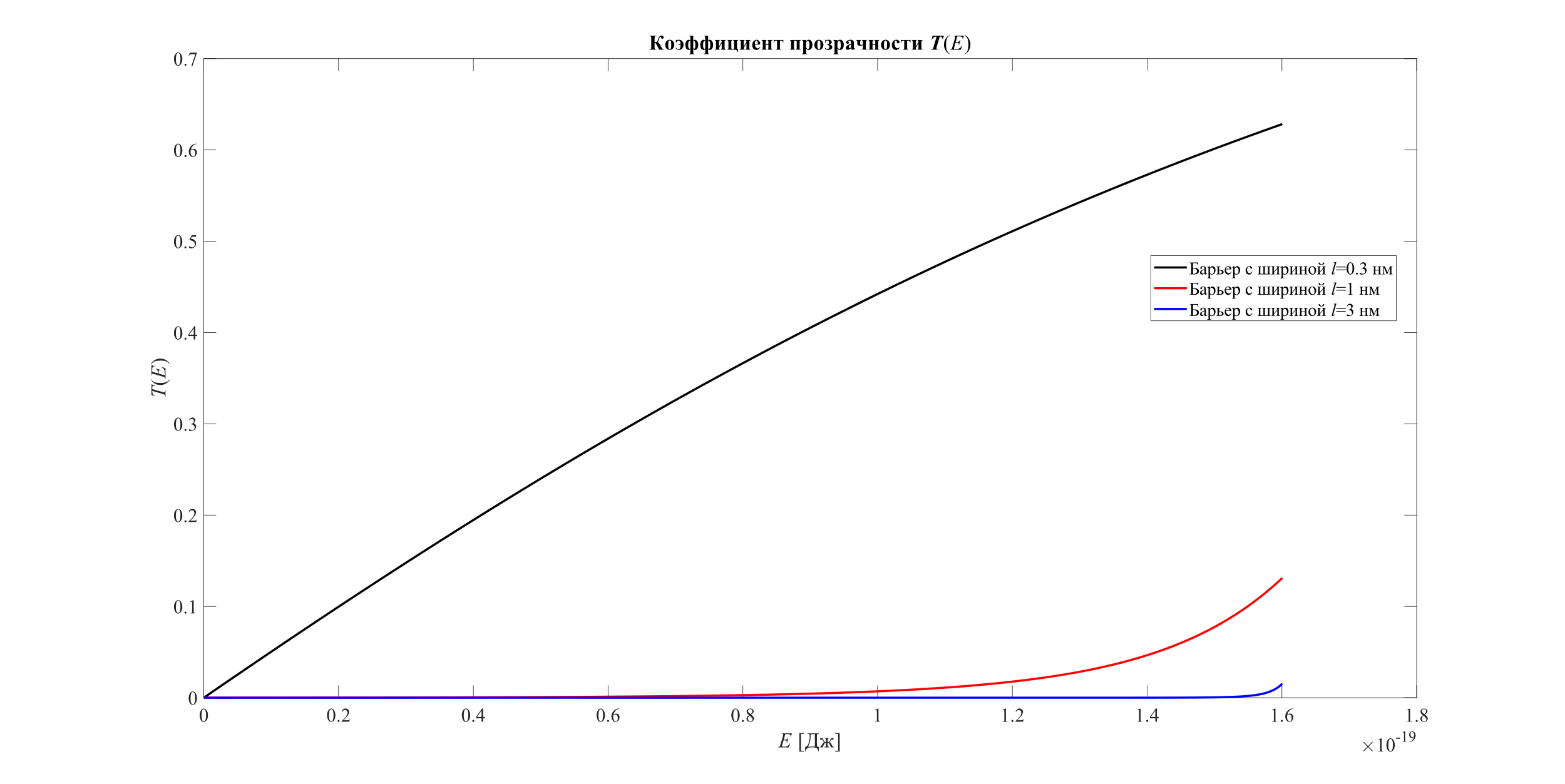
|
Рисунок 3 — График функции T(E) |
Вывод
По полученным графикам T(E) видно, что чем меньше ширина барьера и больше энергия, тем большими получаются значения коэффициента прозрачности, т.е. тем выше вероятность пройти электрону потенциальный рельеф такой формы. При этом для двух последних барьеров с ширинами в 1 и 3 нм соответственно зависимости имеют экспоненциальный характер, а для самого узкого барьера зависимость оказалась отличной от экспоненциальной с резким удалением по значениям от двух остальных зависимостей, но имеющей нелинейный вид хотя и близкий к прямой.
ПРИЛОЖЕНИЕ А
Код программы необходимый для вычислений:
data=zeros(); %массив (матрица) исходных данных. Все величины указаны в СИ
data(1,1)=9.1093837*(10^(-31)); %масса электрона
data(2,1)=1.05457182*(10^(-34)); %постоянная Дирака
data(3,1:3)=[0.3 1 3]*(10^(-9)); %значения l
data(4,1)=5*(10^(-9)); %значение L
data(5,1)=1.60218*(10^(-19)); %значение W1
data(6,1)=0; %значение энергии электрона (W=0)
data(9,1)=0; %значение координаты x=0
data(10,1)=1000; %значение дискретизации для первой задачи
%значения энергий электрона для 0<W<W1 и координаты x (0<x<=L). Диапазон значений энергии и координаты в невозмущённой задаче дискретизирован на 100 уровней (n=100)
for i=2:data(10,1)
data(6,i)=(data(5,1)/data(10,1))*i; %энергия W
data(9,i)=(data(4,1)/data(10,1))*i; %координата x
end
%расчёт значений энергии e=data(7,:) и пси-функции φ=data(8,:) для невозмущённой задачи
for i=1:data(10,1)
data(7,i)=((pi*data(2,1)*i)^2)/(2*data(1,1)*(data(4,1)^2)); %энергия e
data(8,i)=sqrt(2/data(4,1))*sin((i*pi*data(9,i))/(data(4,1))); %пси-функция φ
end
%вычисление W11
for j=1:size(data(3,1:3),2)
data(12,j)=(data(4,1)-data(3,j))/2; %значение a
data(13,j)=(data(4,1)+data(3,j))/2; %значение b
data(11,j)=(data(5,1)*data(3,j))/(data(4,1))+((data(5,1))/(2*pi))*(sin(2*pi*(data(13,j))/(data(4,1)))-sin(2*pi*(data(12,j))/(data(4,1)))); %значение W11
end
%вычисление W1m для m≠1
for j=1:size(data(3,1:3),2)
for i=2:data(10,1)
data(14+(j-1),i)=((data(5,1))/(pi*(1-i)))*(sin((1-i)*((pi*data(13,j))/(data(4,1))))-sin((1-i)*((pi*data(12,j))/(data(4,1)))))-((data(5,1))/(pi*(1+i)))*(sin((1+i)*((pi*data(13,j))/(data(4,1))))-sin((1+i)*((pi*data(12,j))/(data(4,1)))));
end
end
%вычисление значений энергии E и пси-функций ψ для возмущённой задачи
for j=1:size(data(3,1:3),2)
for i=2:(data(10,1)-1)
data(18,j)=((abs(data(14+(j-1),i)))^2)/(data(7,1)-data(7,i))+((abs(data(14+(j-1),i+1)))^2)/(data(7,1)-data(7,i+1)); %сумма для вычисления E
data(19,j)=(data(14+(j-1),i)*data(8,i))/(data(7,1)-data(7,i))+(data(14+(j-1),i+1)*data(8,i+1))/(data(7,1)-data(7,i+1)); %сумма для вычисления пси-функции ψ
end
data(17,j)=data(7,1)+data(11,j)+data(18,j); %вычисление значений энергии E
data(20,j)=data(8,1)+data(19,j); %вычисление значений пси-функций ψ
end
%вычисление коэффициента прозрачности T
for j=1:size(data(3,1:3),2)
for I=1:data(10,1)
data(21,I)=(sqrt(2*data(1,1)*data(6,I)))/data(2,1); %вычисление k
data(22,I)=(sqrt(2*data(1,1)*(data(5,1)-data(6,I))))/data(2,1); %вычисление η
data(23+(j-1),I)=(abs((4*1i*data(21,I)*data(22,I))/(exp(data(22,I)*data(3,j))*((data(22,I)+1i*data(21,I))^2)-exp((-1)*data(22,I)*data(3,j))*((data(22,I)-1i*data(21,I))^2))))^2; %значение T
end
end
%здание ямы с потенциальным барьером
for j=1:size(data(3,1:3),2)
for i=1:data(10,1)
if data(9,i)<=0
data(26+(j-1),i)=10^(-18); %высота барьера. Т.к. барьеры бесконечны, то можно брать любые значения с порядком не много превышающим (не более 2) порядок высоты барьера, чтобы контур потенциального профиля должным образом отображался
%data(29+(j-1),i)=data(17,j);
elseif data(9,i)>0 && data(9,i)<data(12,j)
data(26+(j-1),i)=0;
%data(29+(j-1),i)=data(17,j);
elseif data(9,i)>=data(12,j) && data(9,i)<=data(13,j)
data(26+(j-1),i)=data(5,1);
%data(29+(j-1),i)=data(17,j);
elseif data(9,i)>data(13,j) && data(9,i)<data(4,1)
data(26+(j-1),i)=0;
%data(29+(j-1),i)=data(17,j);
elseif data(9,i)>=data(4,1)
data(26+(j-1),i)=10^(-18); %см. комментарий на строке 53
%data(29+(j-1),i)=data(17,j);
end
end
end
set(0,'DefaultAxesFontSize',18,'DefaultAxesFontName','Times New Roman');
set(0,'DefaultTextFontSize',18,'DefaultTextFontName','Times New Roman');
%контур потенциального профиля с отображением энерг-их ур. для 1-го гл. квантового числа
figure(1)
plot(data(9,1:data(10,1)),data(26+(1-1),1:data(10,1)),'black',data(9,1:data(10,1)),data(26+(2-1),1:data(10,1)),'red',data(9,1:data(10,1)),data(26+(3-1),1:data(10,1)), 'blue','LineWidth',2);
title('Яма с барьером на дне');
legend('Барьер с шириной \it{}l\rm=0.3 нм','Барьер с шириной \it{}l\rm=1 нм','Барьер с шириной \it{}l\rm=3 нм');
xlabel('\it{}x\rm [м]');
ylabel('\it{}W\rm(\it{}x\rm) [Дж]');
%график T(E)
figure(2)
plot(data(6,1:data(10,1)),data(23+(1-1),1:data(10,1)),'black',data(6,1:data(10,1)),data(23+(2-1),1:data(10,1)),'red',data(6,1:data(10,1)),data(23+(3-1),1:data(10,1)),'blue','LineWidth',2);
title('Коэффициент прозрачности \it{}T\rm(\it{}E\rm)');
legend('Барьер с шириной \it{}l\rm=0.3 нм','Барьер с шириной \it{}l\rm=1 нм','Барьер с шириной \it{}l\rm=3 нм');
xlabel('\it{}E\rm [Дж]');
ylabel('\it{}T\rm(\it{}E\rm)');
Таганрог 2022