
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
«Южный федеральный университет»
Институт нанотехнологий, электроники и приборостроения
ОТЧЁТ
О ПРАКТИЧЕСКОЙ РАБОТЕ №3
Связанные состояния частицы в конечной яме
по дисциплине:
«Квантовая механика»
СОДЕРЖАНИЕ
1 Условие задачи 3
2 Решение задачи 4
Вывод 16
ПРИЛОЖЕНИЕ А 16
1 Условие задачи
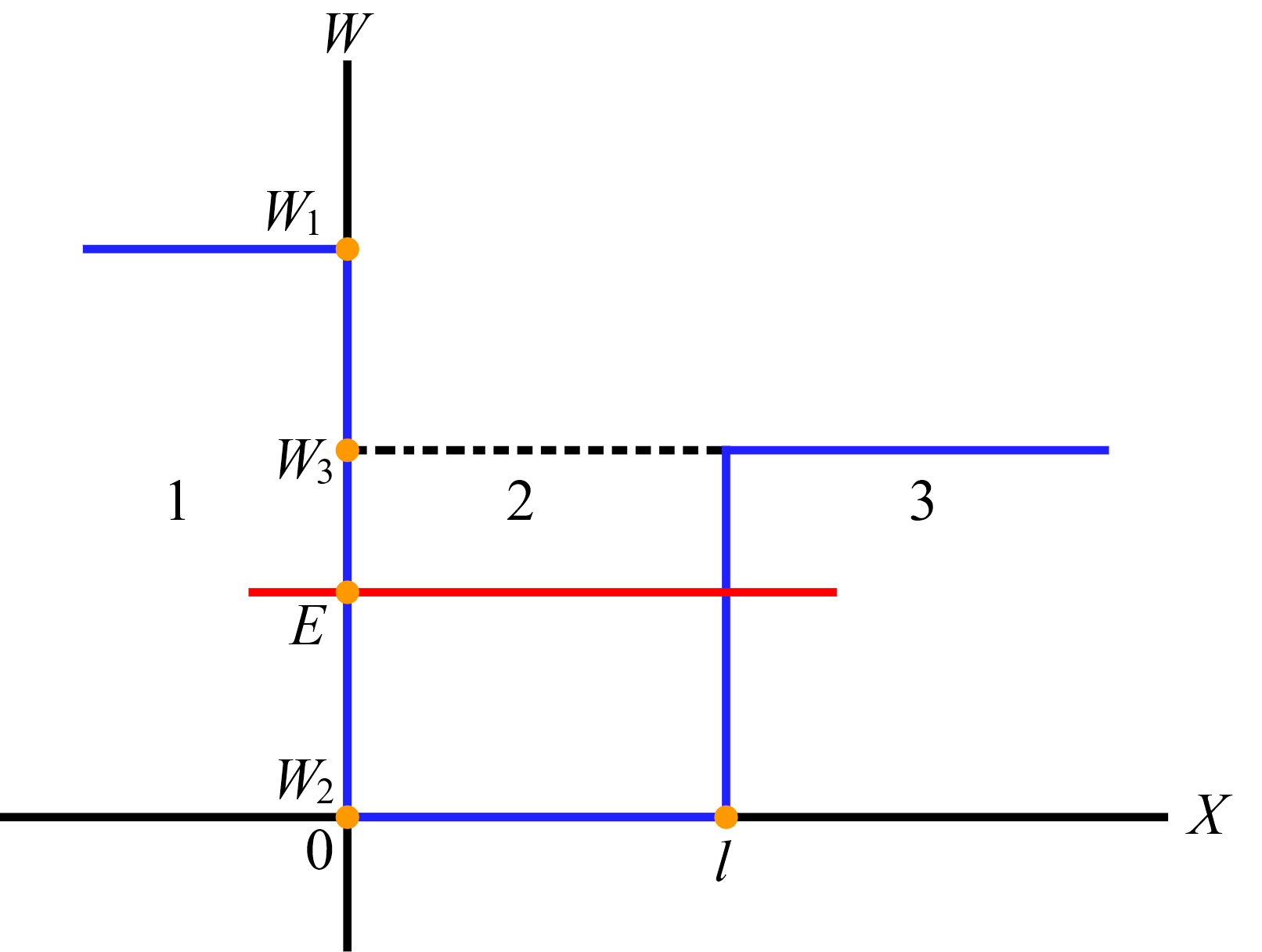
Дан электрон, который может совершать одномерное движение вдоль оси X (рисунок 1), находясь при этом в потенциальном поле W(x), W — потенциальная энергия.
|
Рисунок 1 — Потенциальная яма |
В
этом пространстве имеется потенциальная
яма, расположенная в области, заданной
следующим условием:
 ,
где
,
где
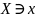 — координата частицы. При этом для всех
— координата частицы. При этом для всех
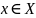 :
:
 (область 1),
(область 1),
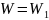 ;
для всех
:
(область 2),
;
для всех
:
(область 2),
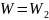 ;
для всех
:
;
для всех
:
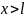 (область 3),
(область 3),
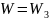 .
А при
.
А при
 ,
,
 ;
;
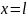 ,
,
 .
И к тому же для всех
,
.
И к тому же для всех
,
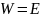 — энергия электрона. При этом
— энергия электрона. При этом
 .
.
Необходимо
построить графики зависимости энергии
E электрона от главного
квантового числа n, а
также графики функций
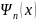 и
и
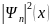 (т.е. графики функций: пси-функции и
вероятности обнаружения электрона от
его координаты) в диапазоне:
(т.е. графики функций: пси-функции и
вероятности обнаружения электрона от
его координаты) в диапазоне:
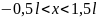 в соответствии с вариантом значения l
для всех
в соответствии с вариантом значения l
для всех
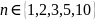 и для симметричной и несимметричной
потенциальной ямы.
и для симметричной и несимметричной
потенциальной ямы.
Индивидуальный вариант условий приведён в таблице 1.
Таблица 1 — Индивидуальный вариант условий
Номер варианта |
l [нм] |
W1 [эВ] |
W3 [эВ] |
1 |
0,5 |
8 |
4 |
2 Решение задачи
Движение частицы в потенциальном поле будет характеризоваться некоторой энергетической величиной E, которая называется полной энергией частицы и равна сумме потенциальной W и кинетической T энергии частицы:

Согласно постулатам квантовой механики:
1) каждой наблюдаемой физической величине в квантовой механике соответствует эрмитов оператор;
2) собственные функции этого эрмитова оператора есть волновые функции системы в соответствующем состоянии;
3) собственные значения этого эрмитова оператора равны тем значениям физической величины, которые могут быть получены в эксперименте.
Поэтому
потенциальная энергия будет описываться
с помощью оператора потенциальной
энергии
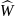 ,
для которого будут выполняться два
последних условия, приведённые выше.
Кроме этого, энергия частицы задаётся
не только потенциальной энергией, но и
кинетической T, которой
также будет соответствовать эрмитов
оператор кинетической энергии
,
для которого будут выполняться два
последних условия, приведённые выше.
Кроме этого, энергия частицы задаётся
не только потенциальной энергией, но и
кинетической T, которой
также будет соответствовать эрмитов
оператор кинетической энергии
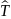 .
Эрмитов оператор, соответствующий
полной энергии E
частицы, называется оператором Гамильтона
.
Эрмитов оператор, соответствующий
полной энергии E
частицы, называется оператором Гамильтона
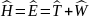 .
У оператора Гамильтона есть собственные
функции, которыми являются волновые
(или — пси-)функции
.
У оператора Гамильтона есть собственные
функции, которыми являются волновые
(или — пси-)функции
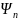 и собственные значения, которыми являются
значения полной энергии системы
и собственные значения, которыми являются
значения полной энергии системы
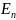 .
Поэтому для него будет выполняться
следующее операторное равенство:
.
Поэтому для него будет выполняться
следующее операторное равенство:
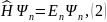
которое можно рассматривать как операторное уравнение, если искомой величиной будет пси-функция.
Оператор кинетической энергии имеет вид:

где
ħ — постоянная Дирака, m
— масса квантово-механической системы
(электрона),
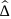 — лапласиан, он равен:
— лапласиан, он равен:

С учётом (3, 2) и определения оператора Гамильтона можно записать:
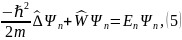
полученное выражение называется стационарным уравнением Шредингера, поскольку пси-функция не изменяется во времени, поэтому выражение (5) следует записать так:
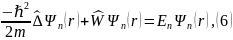
где r — радиус-вектор. Для одномерного случая, например, когда частица может двигаться только вдоль координатной оси X, имеем:
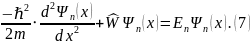
Т. о., мы получили одномерное стационарное уравнение Шредингера, этим уравнением и решается задача о движении частицы в потенциальной яме.
Чтобы решить уравнение (7) необходимо найти все такие значения функции , при которых бы выполнялось данное равенство. Для начала сделаем пару изменений. Преобразуем уравнение (7) к виду:
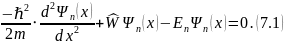
Хотелось
бы упростить уравнение (7.1) преобразовав
его часть
 к более простому виду. Это можно сделать.
к более простому виду. Это можно сделать.
Выражение
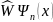 является действием оператора потенциальной
энергии на пси-функцию, результатом
чего будет некоторая функция
является действием оператора потенциальной
энергии на пси-функцию, результатом
чего будет некоторая функция
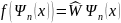 ,
вид которой определяется как функцией
,
так и оператором
.
В целом вид оператора
неизвестен, поэтому нельзя сказать об
каком-нибудь аналитическом виде функции
f тем более, что и сам
вид функции
также неизвестен. Необходимо привлечь
дополнительные сведения об операторе
потенциальной энергии. Сама по себе
потенциальная энергия W
является функцией координаты r
и времени t
,
вид которой определяется как функцией
,
так и оператором
.
В целом вид оператора
неизвестен, поэтому нельзя сказать об
каком-нибудь аналитическом виде функции
f тем более, что и сам
вид функции
также неизвестен. Необходимо привлечь
дополнительные сведения об операторе
потенциальной энергии. Сама по себе
потенциальная энергия W
является функцией координаты r
и времени t
 .
Поэтому её оператор будет действовать
на любую другую функцию, как умножение
.
Поэтому её оператор будет действовать
на любую другую функцию, как умножение
 на данную функцию. Получается, что
на данную функцию. Получается, что
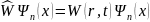 .
Тогда выражение
можно свести к виду:
.
Тогда выражение
можно свести к виду:
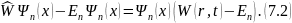
Т.о., уравнение (7.1) с учётом (7.2) можно преобразовать к виду:

Получается,
что нам необходимо решить однородное
дифференциальное уравнение второго
порядка с переменные коэффициентами,
в котором первая производная
равна нулю
 .
.
Общим решением обыкновенного дифференциального уравнения (7.3) второго порядка, соответствующего общему виду:

где y — неизвестная функция от аргумента x, называется такая функция, что:
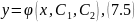
где C1, C2 — произвольные постоянные, которая при любом фиксированном наборе этих постоянных определяет решение уравнения (7.4).
Заметим
также, что решение (7.3) упроститься, если
его расписать для каждой из трёх областей
нашей задачи (рисунок 1). В области 1
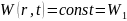 ;
в области 2
;
в области 2
 ;
в области 3
;
в области 3
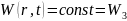 .
.
Т.о., исходное уравнение (7.3) выливается в систему из трёх однородных (линейных) обыкновенных дифференциальных уравнений второго порядка:
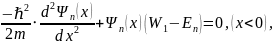
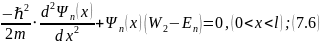
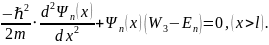
Каждое из этих уравнений системы будет подчиняться общему виду общего решения:
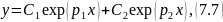
где C1, C2 — некоторые константы; y — искомая функция; p1, p2 — корни характеристического уравнения, которое, для уравнений второго порядка, имеет общий вид:
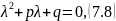
где
λ — неизвестное уравнения, которой
заменяется производная порядка,
соответствующего показателю степени
неизвестной; p, q
— коэффициенты перед искомыми функциями:
p перед первой
производной искомой функции (в нашем
случае она равна нулю), а q
перед самой искомой функцией. Найдём
эти корни характеристического уравнения
для уравнений нашей системы (7.6). Для
начала приведём эти уравнения к
необходимому виду. Домножим каждое из
уравнений системы (7.6) на множитель
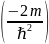 ,
получим:
,
получим:
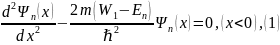
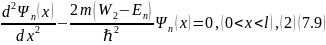
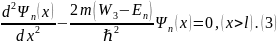
Составим характеристические уравнения для наших уравнений:
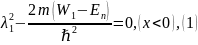
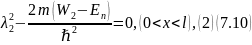
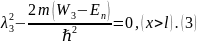
Неизвестной
λ в степени 1 нет, т.к.
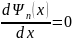 .
Уравнения системы (7.10) решатся следующим
образом:
.
Уравнения системы (7.10) решатся следующим
образом:
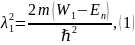
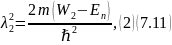

поэтому
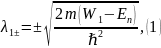
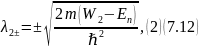
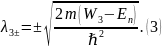
Т.к. En (энергия электрона) для всех областей одна и та же, то заменим En на E.
Поскольку
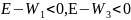 ,
то это значит, что
,
то это значит, что
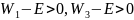 ,
поэтому корни
,
поэтому корни
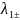 и
и
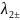 будут действительными. А вот для
дело обстоит иначе, у него
будут действительными. А вот для
дело обстоит иначе, у него
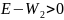 ,
т.е.
,
т.е.
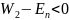 ,
поэтому корни
будут комплексными. Т.о., систему (7.12)
можно записать, как:
,
поэтому корни
будут комплексными. Т.о., систему (7.12)
можно записать, как:
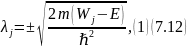
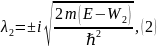
где
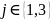 .
.
Поэтому с учётом (7.7) и (7.12) решение уравнения Шрёдингера для трёх областей примет вид:

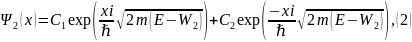
где . Выражение (2) в (7.13) можно записать и в действительной форме, как:
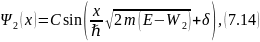
где C и δ — некоторые константы.
В итоге имеем следующее общее решение уравнения Шрёдингера для трёх областей:
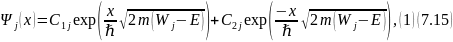
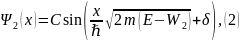
где .
Чтобы
полностью описать движение частицы в
потенциальной яме с энергией, соответствующе
красной линии на рисунке 1, необходимо
найти частные виды уравнения (8) для
областей 1, 2 и 3, затем сшить пси-функции
в точках скачка потенциала:
 и потребовать непрерывности первых
производных пси-функции.
и потребовать непрерывности первых
производных пси-функции.
Исходя
из физического смысла волновой функции
следует считать, что
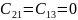 — модуль квадрата пси-функции нормирован
на единицу, больше неё он быть не может,
но функция
— модуль квадрата пси-функции нормирован
на единицу, больше неё он быть не может,
но функция
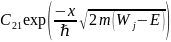 в пределе равна
в пределе равна
 ;
функция
;
функция
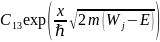 ,
также в пределе равна
.
Тогда система (7.15) примет вид:
,
также в пределе равна
.
Тогда система (7.15) примет вид:
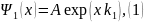

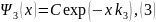
где
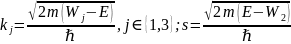 .
.
Запишем теперь условия сшивки:
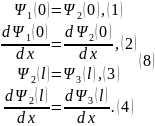
С учётом (7.16) выражения (8) примут вид:

Решая
полученную систему относительно s
и
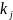 ,
получим:
,
получим:
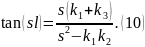
Величины s, kj зависят от энергии частицы, поэтому полученное уравнение является трансцендентным и для его решения применим графический метод.
Не
нарушая общности, можно считать, что
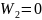 .
Введём безразмерные переменные:
.
Введём безразмерные переменные:

С учётом (7.16) и введённых обозначений, получим:
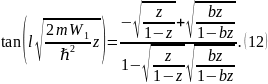
Это трансцендентное уравнение можно решать графически. Для получения более точных значений корней уравнения можно применить какой-либо численный метод решения уравнений, например, метод дихотомии.
Рассмотрим сначал решение уравнения
для случая
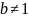 ,
то есть для несимметричной ямы
,
то есть для несимметричной ямы
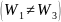 .
Графики правой и левой частей уравнения
(12) (рисунок 2) будут строиться в
интернет-приложении Desmos.
Ссылка: https://www.desmos.com/calculator/pmtc5x3uz3?lang=ru
на построенные графики в этом ресурсе.
.
Графики правой и левой частей уравнения
(12) (рисунок 2) будут строиться в
интернет-приложении Desmos.
Ссылка: https://www.desmos.com/calculator/pmtc5x3uz3?lang=ru
на построенные графики в этом ресурсе.
|
Рисунок 2 — Графическое решение для несимметричной ямы |
Заметим
также, что значения z
не могут превышать значения 1 и должны
быть больше нуля. Т.о., для нашего случая
z будем искать в
следующем диапазоне:
 .
Найденные значения z
получились следующими:
.
Найденные значения z
получились следующими:
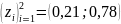 .
.
С помощью, полученных значений z можно найти энергии электрона для соответствующего энергетического уровня n, воспользовавшись уравнением (11):
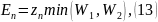
при этом большему номеру энергетического уровня должно соответствовать большее значение z.
Теперь
рассмотрим решение для симметричной
ямы
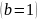 (рисунок 3). Ссылка:
https://www.desmos.com/calculator/zxqxqfjpnv?lang=ru
на построенные графики в этом ресурсе.
(рисунок 3). Ссылка:
https://www.desmos.com/calculator/zxqxqfjpnv?lang=ru
на построенные графики в этом ресурсе.
|
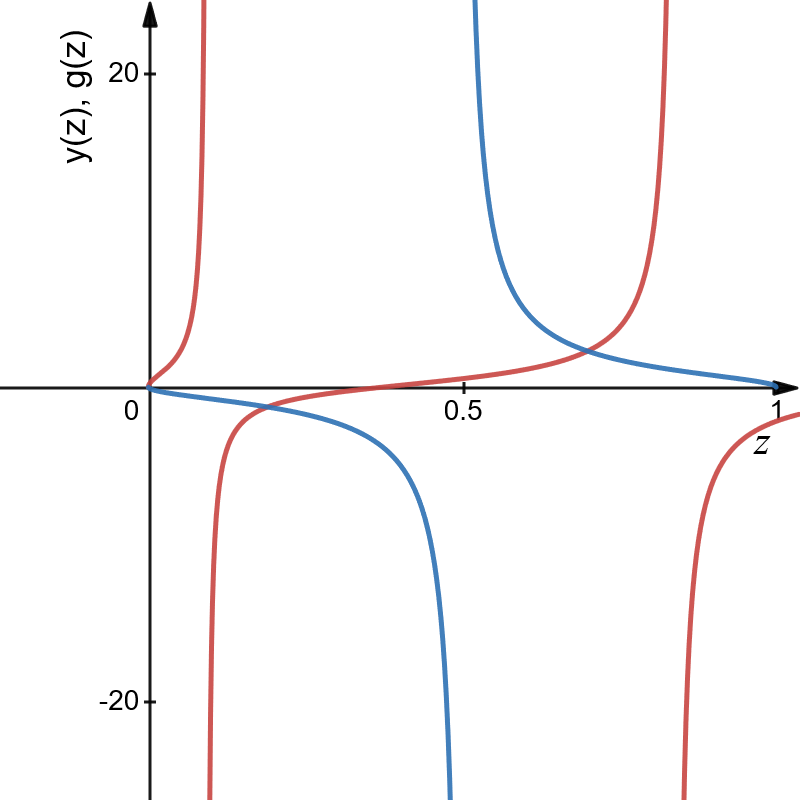
Рисунок 3 — Графическое решение для симметричной ямы |
Найденные значения z
получились следующими:
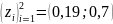 .
.
Чтобы найти явный вид волновой функции, нужно определить коэффициенты A, B и C, а также фазу δ. Для этого снова рассмотрим систему уравнений, возникающую из условий непрерывности волновой функции и её производной.
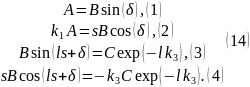
Из которой можно получить, что:

где n — индекс номера энергетического уровня (иначе, главное квантовое число).
Далее можно найти, что:


Для определения константы A воспользуемся условием нормировки волновой функции:
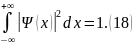
Тогда с учётом (16—18) можно получить:
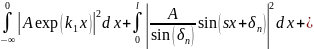
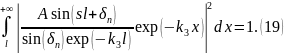
Первый интеграл примет вид:
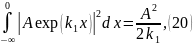
второй:

третий:

Т.о., выражение (16) примет вид:

из которого можно получить:
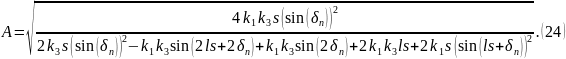
Расчёт энергий En, пси-функций, вероятностей и построение их графиков будет произведено в MATLAB, код программы необходимый для этих вычислений приведён в приложении А.
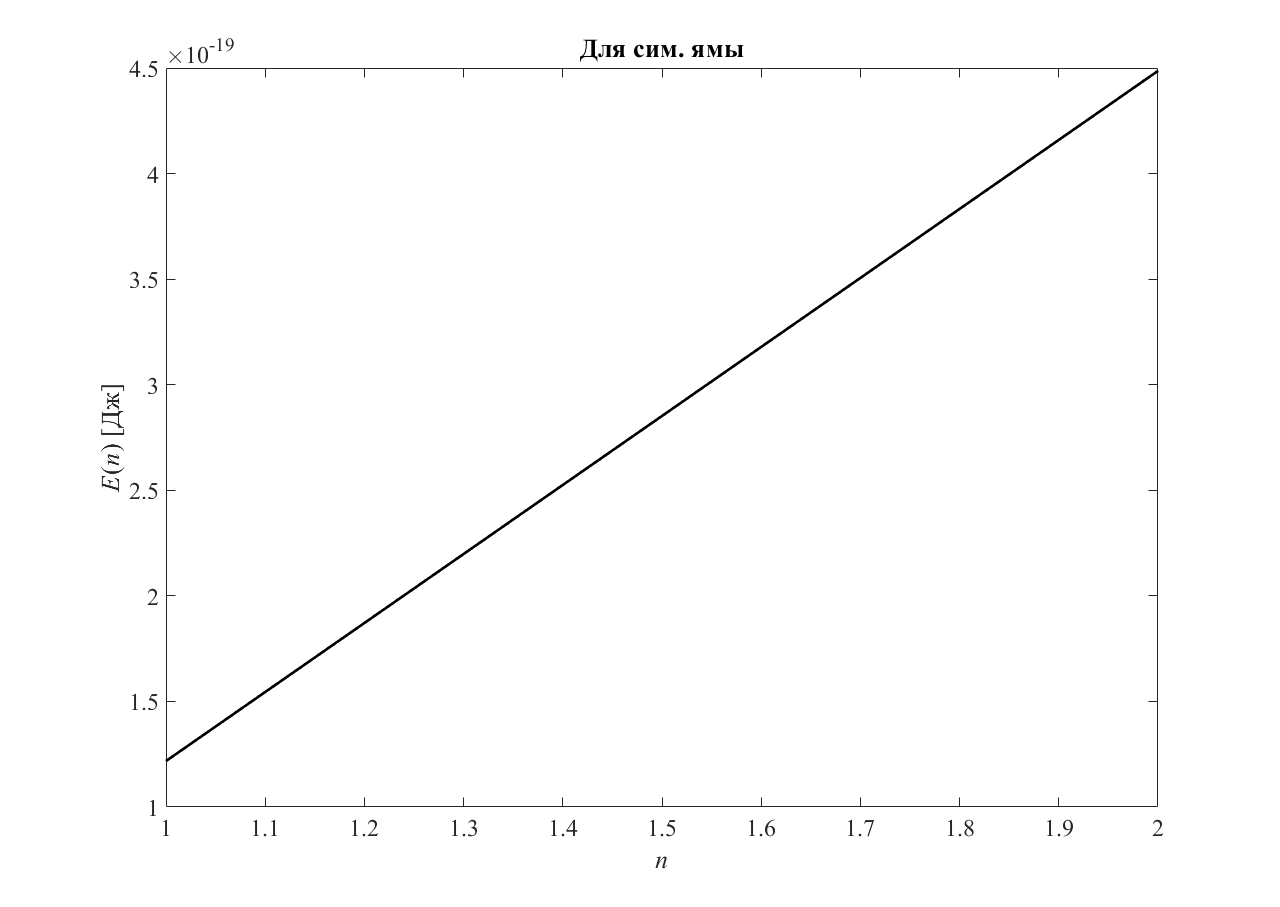
График
 — зависимости энергии от энергетического
уровня для сим. ямы приведён на рисунке
3.
— зависимости энергии от энергетического
уровня для сим. ямы приведён на рисунке
3.
|
Рисунок 3 — График для сим. ямы |
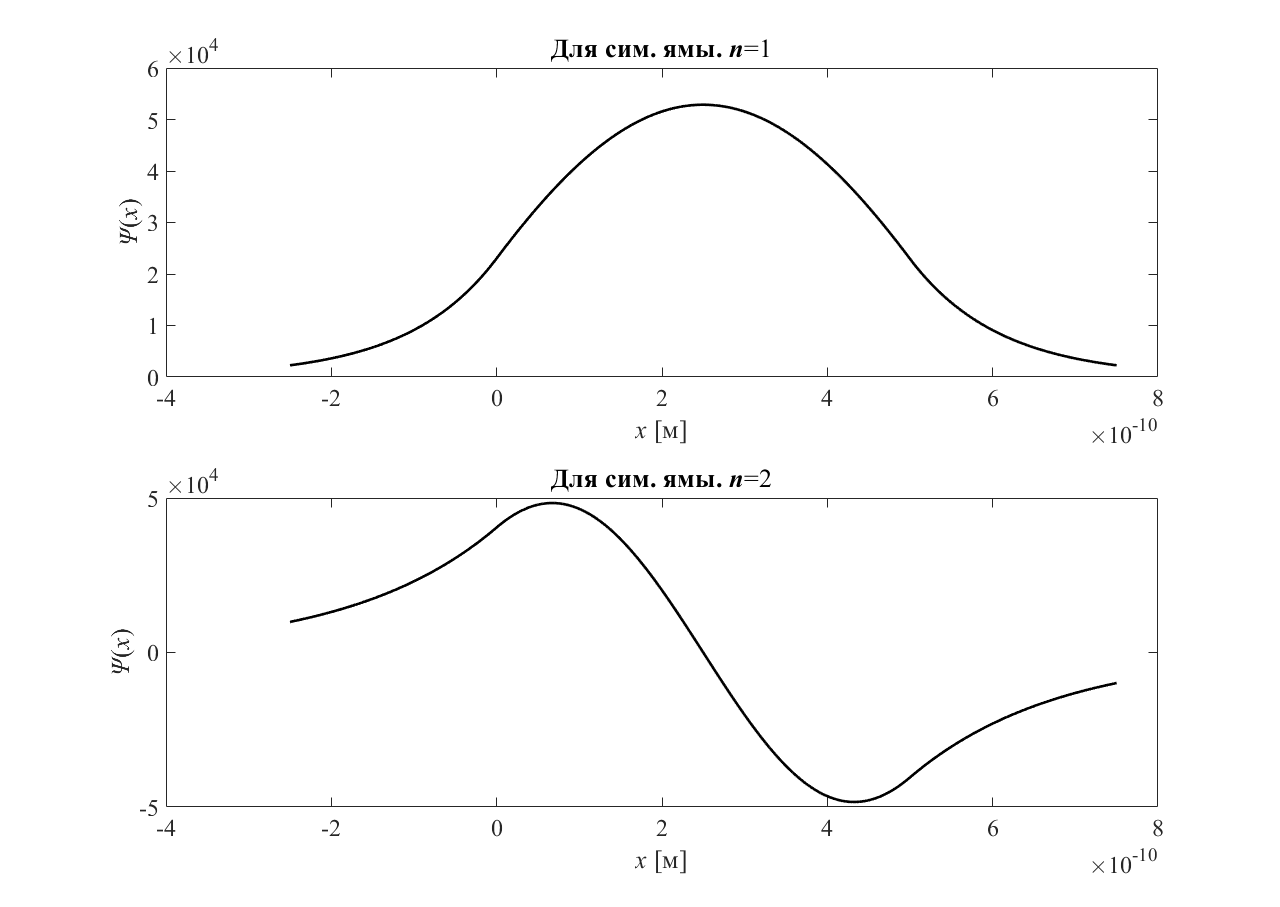
График
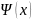 — зависимости пси-функции от координаты
электрона для
— зависимости пси-функции от координаты
электрона для
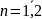 для сим. ямы приведён на рисунке 4.
для сим. ямы приведён на рисунке 4.
|
Рисунок 4 — График для сим. ямы |
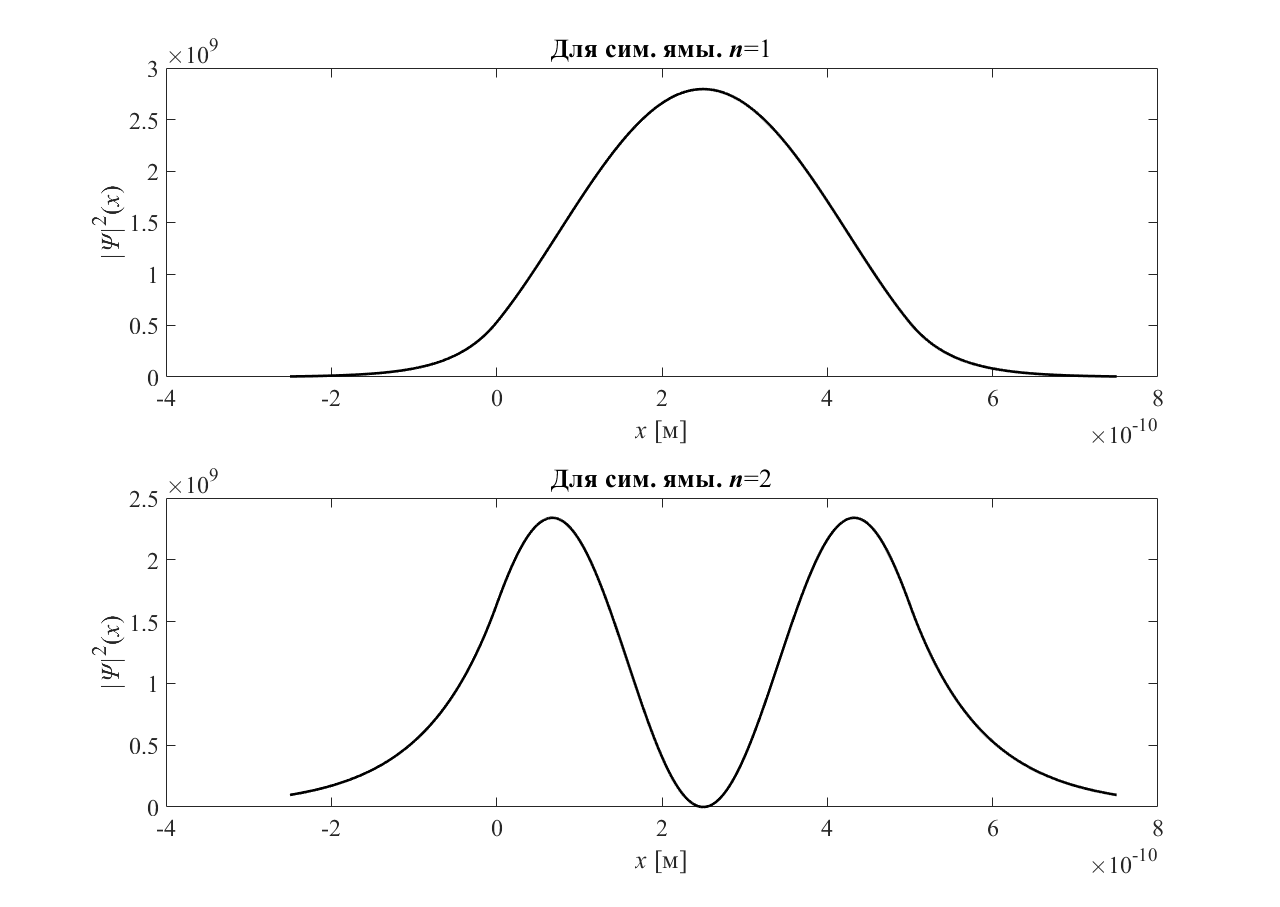
График
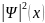 — зависимости квадрата пси-функции от
координаты электрона для
для сим. ямы приведён на рисунке 5.
— зависимости квадрата пси-функции от
координаты электрона для
для сим. ямы приведён на рисунке 5.
|
Рисунок 5 — График для сим. ямы |
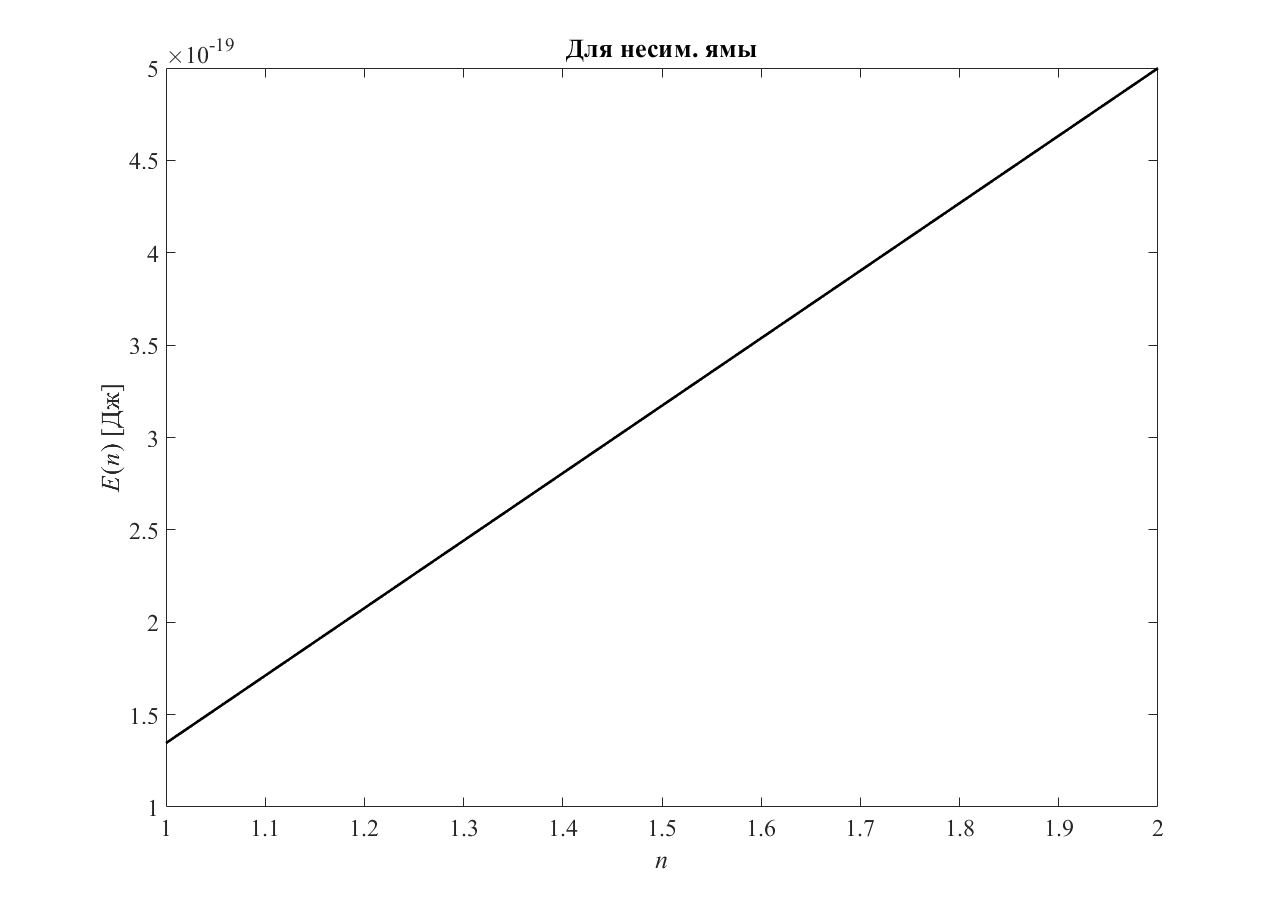
График — зависимости энергии от энергетического уровня для несим. ямы приведён на рисунке 6.
|
Рисунок 6 — График для несим. ямы |
График — зависимости пси-функции от координаты электрона для для несим. ямы приведён на рисунке 7.
|
Рисунок 7 — График для несим. ямы |
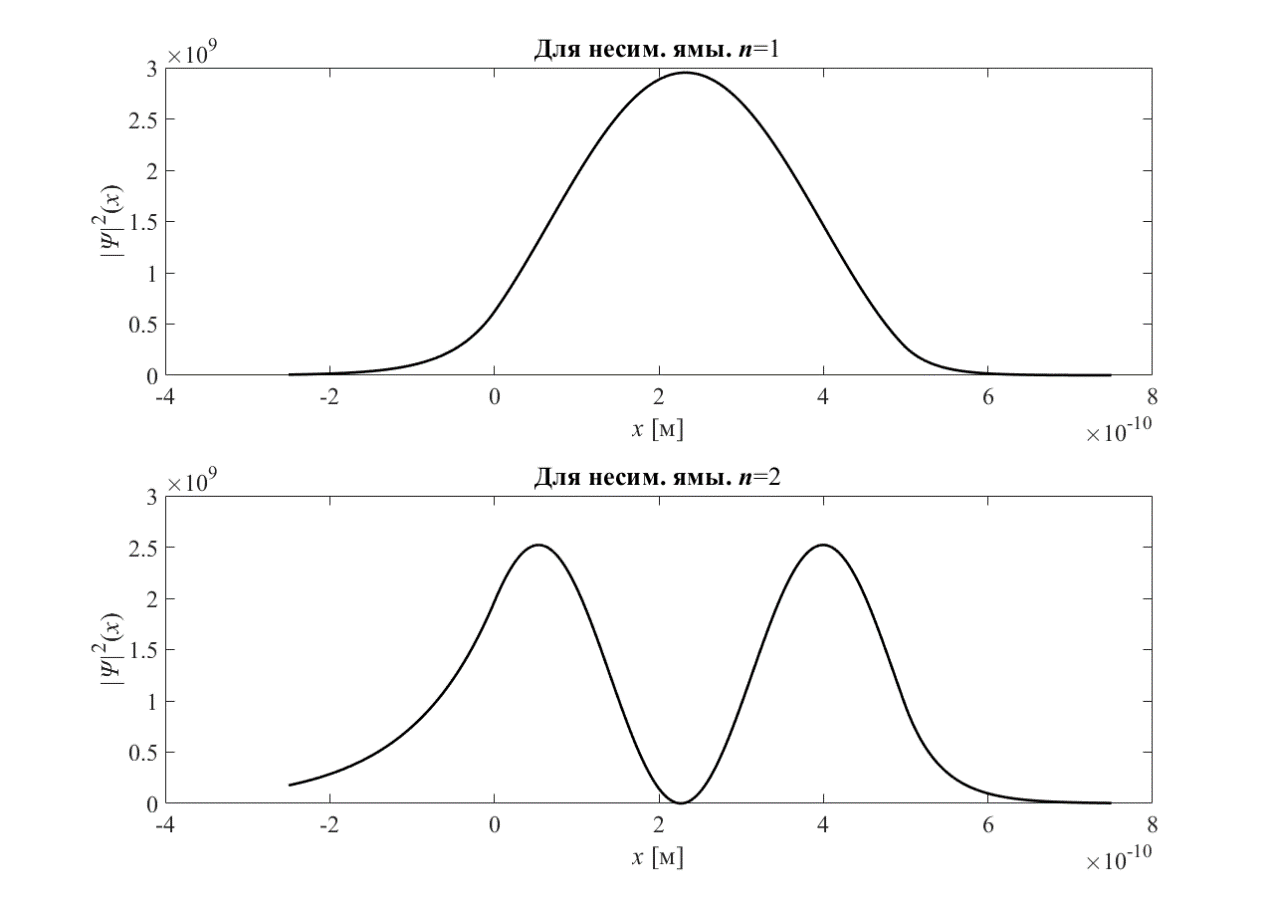
График — зависимости квадрата пси-функции от координаты электрона для для несим. ямы приведён на рисунке 8.
|
Рисунок 8 — График для несим. ямы |
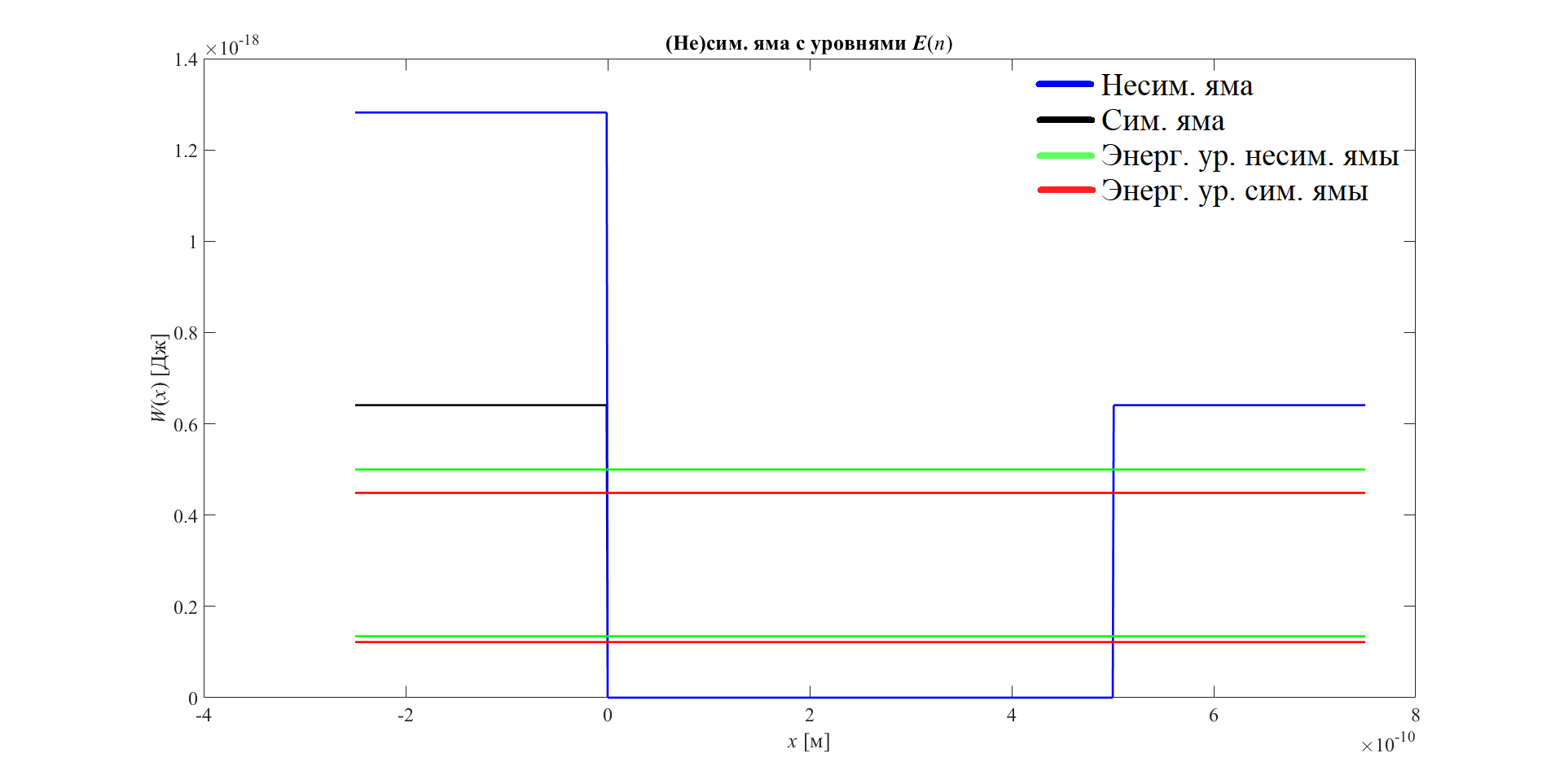
График (не)симметричной ямы с уровнями энергий приведён на рисунке 9.
|
Рисунок 9 — График
|
Вывод
В результате выполнения работы было
получено по два корня уравнения как для
симметричной ямы, так и для несимметричной
необходимые для вычисления энергетических
уровней энергии электрона. Из выше
приведённых рисунков графиков пси-функций
видно, что вероятность обнаружить
частицу в заданной координате увеличивается
по экспоненциальному закону при
стремлении координаты к тому значению,
в котором находится левый барьер. После,
вероятность внутри ямы приобретает
периодический вид близкий к виду функции
 .
Затем плавно переходит в вид убывающей
экспоненты. Приведенные особенности
характеры для обеих ям.
.
Затем плавно переходит в вид убывающей
экспоненты. Приведенные особенности
характеры для обеих ям.
Возникшее взаимное смещение энергетических уровней вызвано асимметрией барьеров у несимметричной ямы. Величина этого смещения зависит от разности энергетических уровней барьеров.



 для (не)сим. ямы
для (не)сим. ямы