Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное

учреждение высшего образования

«Южный федеральный университет»

Институт нанотехнологий, электроники и приборостроения

ОТЧЁТ

О ПРАКТИЧЕСКОЙ РАБОТЕ №2

Частица в потенциальной яме с конечными стенками

по дисциплине:

«Квантовая механика»

СОДЕРЖАНИЕ

1 Условие задачи 3

2 Решение задачи 3

Вывод 7

ПРИЛОЖЕНИЕ А 7

1 Решение стационарного уравнения Шрёдингера 7

2 Решение системы (13) 10

ПРИЛОЖЕНИЕ Б 12

1 Условие задачи

Дана некоторая микроскопическая частица (далее — частица), которая может совершать одномерное движение вдоль оси X (рисунок 1), находясь при этом в потенциальном поле W(x), W — потенциальная энергия.

Рисунок 1 — Потенциальная яма

В этом пространстве имеется потенциальная яма, расположенная в области, заданной следующим условием: , где — координата частицы. При этом для всех (область 1), ; для всех (область 2), ; для всех (область 3), . А при , ; , . И к тому же для всех , .

Необходимо построить графики зависимости коэффициента прохождения T(E) от энергии частицы для симметричной и несимметричной потенциальной ямы.

Индивидуальный вариант условий приведён в таблице 1.

Таблица 1 — Индивидуальный вариант условий

Номер варианта	n	m	L, нм	W1, эВ	W3, эВ	V, эВ
1	2	1	0,5	−8	−4	5

2 Решение задачи

Движение частицы в потенциальном поле будет характеризоваться некоторой энергетической величиной E, которая называется полной энергией частицы и равна сумме потенциальной W и кинетической T энергии частицы:

Согласно постулатам квантовой механики:

1) каждой наблюдаемой физической величине в квантовой механике соответствует эрмитов оператор;

2) собственные функции этого эрмитова оператора есть волновые функции системы в соответствующем состоянии;

3) собственные значения этого эрмитова оператора равны тем значениям физической величины, которые могут быть получены в эксперименте.

Поэтому потенциальная энергия будет описываться с помощью оператора потенциальной энергии , для которого будут выполняться два последних условия, приведённые выше. Кроме этого, энергия частицы задаётся не только потенциальной энергией, но и кинетической T, которой также будет соответствовать эрмитов оператор кинетической энергии . Эрмитов оператор, соответствующий полной энергии E частицы, называется оператором Гамильтона . У оператора Гамильтона есть собственные функции, которыми являются волновые (или — пси-)функции и собственные значения, которыми являются значения полной энергии системы . Поэтому для него будет выполняться следующее операторное равенство:

которое можно рассматривать как операторное уравнение, если искомой величиной будет пси-функция.

Оператор кинетической энергии имеет вид:

где ħ — постоянная Дирака, m — масса квантово-механической системы (частицы), — лапласиан, он равен:

С учётом (3, 2) и определения оператора Гамильтона можно записать:

полученное выражение называется стационарным уравнением Шредингера, поскольку пси-функция не изменяется во времени, поэтому выражение (5) следует записать так:

где r — радиус-вектор. Для одномерного случая, например, когда частица может двигаться только вдоль координатной оси X, имеем:

Т. о., мы получили одномерное стационарное уравнение Шредингера, этим уравнением и решается задача о движении частицы в потенциальной яме.

Решение данного уравнения приведено в ПРИЛОЖЕНИИ А, 1 Решение стационарного уравнения Шрёдингера. Полученное решение имеет вид:

где .

Вид функции (8) является суммой двух волн, одна из которых набегает на потенциальный барьер, а другая отражается от него. Поэтому, чтобы формула (8) имела физический смысл её необходимо модифицировать. Для области 1 будем рассматривать её, как суперпозицию волны (с амплитудой C₂₁), налетающей из области отрицательных значений координат и волны (с амплитудой C₁₁), отражённой от потенциальной ямы. 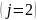Для области 2 можно также рассматривать, как суперпозицию волны (с амплитудой C₂₂), налетающей из области отрицательных значений координат и волны (с амплитудой C₁₂), отражённой от второй границы потенциальной ямы. Для области 3 можно также рассматривать, как суперпозицию двух волн. Но если исходная волна (с амплитудой C₂₃) (частица) налетает из «минус бесконечности», то из «плюс бесконечности» налетать частица не может. Отражаться там тоже не от чего. Поэтому амплитуду волны (с амплитудой C₁₃), движущейся из «плюс бесконечности» влево положим равной нулю . Т.о., уравнение (8) преобразуется к виду:

Дадим теперь определение коэффициента отражения R. Он равен вероятности того, что частица, отразившись от ямы, начнёт двигаться в сторону отрицательных координат. Он равен квадрату модуля отношения амплитуд отражённой и падающей волн:

где .

Коэффициент прохождения T частицы равен квадрату модуля отношения амплитуд прошедшей и падающей волн:

Исходя из физического смысла коэффициентов:

Теперь необходимо сшить пси-функцию в точках, где она не определена — границы областей 1, 2, 3: 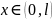. Сшивка волновой функции требует её непрерывности и её первой производной на границах областей, т.е. для , а это значит, что:

Решение системы (13) приведено в ПРИЛОЖЕНИИ А, 2 Решение системы (13), из которой было получено выражение (13.13):

где .

В случае, когда яма симметричная это значит, что .

Потенциальную яму расположим так, чтобы уровень (рисунок 1), а W₂ и W₃ находились в области отрицательных энергий.

Для построения необходимых графиков воспользуемся MATLAB’ом. Код программы необходимый для построения графиков приведён в ПРИЛОЖЕНИИ Б.

Значения констант, использованных в вычислениях приведены в таблице 2. В качестве частицы был взят электрон.

Таблица 2 — Данные для вычислений

Величина	Значение
Масса электрона [кг]	9,10∙10−31
Постоянная Дирака [м2∙кг/с]	1,05∙10−34
W2 (W1 в таблице 1) [Дж]	−1.282∙10−18
W3 [Дж]	−6.409∙10−19
W1 [Дж]	0
W0 [Дж]	0—300∙10−19

Случаи с несимметричной и симметричной ямами приведены на рисунке 2.

Рисунок 2 — (Не)симметричная яма

Вывод

Построенные графики зависимостей коэффициентов прохождения от энергии частицы для (не)симметричной ямы имеют различные виды. Это связано с тем, что в симметричной яме, вероятность прохождения частицы через барьер больше, чем в несимметричной при данном значении энергии частицы. Но с ростом энергии частицы, вероятность пройти барьер асимптотически растет и в предел, она равна единице.