Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
«Южный федеральный университет»
Институт нанотехнологий, электроники и приборостроения
ОТЧЁТ
О ПРАКТИЧЕСКОЙ РАБОТЕ №1
Частица в бесконечно глубокой потенциальной яме
по дисциплине:
«Квантовая механика»
СОДЕРЖАНИЕ
1 Условие задачи 3
2 Решение задачи 3
Вывод 9
ПРИЛОЖЕНИЕ А 9
1 Условие задачи
Дан электрон, который может совершать одномерное движение вдоль оси x между бесконечными стенками и на дне потенциальной ямы (рисунок 1).
|
Рисунок 1 — Потенциальная яма |
По условию задачи необходимо:
1)
построить график зависимости
(разницы энергий между n-м и m-м
квантовыми уровнями) от ширины
потенциальной ямы L в диапазоне от
0,5 до 5 нм;
2)
построить графики зависимости
и
в диапазоне:
нм при заданном L для
каждого n в диапазоне
от 1 до 6.
Индивидуальный вариант условий приведён в таблице 1.
Таблица 1 — Индивидуальный вариант условий
Номер варианта |
Тип частицы |
n |
m |
L, нм |
W1, эВ |
W3, эВ |
V, эВ |
1 |
электрон |
2 |
1 |
0,5 |
8 |
4 |
5 |
2 Решение задачи
Найдём выражение, определяющее зависимость энергии электрона от значения главного квантового числа n.
Так как электрон находится на дне потенциальной ямы с бесконечными стенками, то потенциальная энергия W внутри ямы равна нулю, а снаружи — бесконечности (+∞), поэтому можно записать, что:
где W1 и W3 — значения потенциальной энергии (электрона) снаружи ямы (области 1 и 3, отмеченные на рисунке 1), а W2 — значение потенциальной энергии внутри ямы (область 2 на рисунке 1).
Согласно постулатам квантовой механики:
1) каждой наблюдаемой физической величине в квантовой механике соответствует эрмитов оператор;
2) собственные функции этого эрмитова оператора есть волновые функции системы в соответствующем состоянии;
3) собственные значения этого эрмитова оператора равны тем значениям физической величины, которые могут быть получены в эксперименте.
Поэтому
потенциальная энергия будет описываться
с помощью оператора потенциальной
энергии
,
для которого будут выполняться два
последних условия, приведённые выше.
Кроме этого, энергия электрона задаётся
не только потенциальной энергией, но и
кинетической T, которой
также будет соответствовать эрмитов
оператор кинетической энергии
.
Сумма этих энергий задаёт т. н. полную
энергию системы
,
в данном случае, электрона. Эрмитов
оператор, соответствующий полной энергии
системы (электрона), называется оператором
Гамильтона
.
У оператора Гамильтона есть собственные
функции, которыми являются волновые
(или — пси-)функции
и собственные значения, которыми являются
значения полной энергии системы
.
Поэтому для него будет выполняться
следующее операторное уравнение:
в котором искомой величиной будет пси-функция.
Оператор кинетической энергии имеет вид:
где
ħ — постоянная Дирака, m
— масса квантово-механической системы
(электрона),
— лапласиан, он равен:
С учётом (3, 2) и определения оператора Гамильтона можно записать:
полученное выражение называется стационарным уравнением Шредингера, поскольку пси-функция не изменяется во времени, поэтому выражение (5) следует записать так:
где r — радиус-вектор. Для одномерного случая, например, когда частица может двигаться только вдоль координатной оси x, имеем:
Т. о., мы получили одномерное стационарное уравнение Шредингера, этим уравнением и решается задача о движении частицы в потенциальной яме.
Так
как в областях 1 и 3 (рисунок 1) потенциальная
энергия одинакова, то и решение уравнения
(7) будет одинаковым. Поскольку в
интервалах:
и
потенциальные энергии равны
,
то единственным решением уравнения (7)
будет то значение пси-функции, при
котором
.
В
области 2
,
поэтому уравнение (7) примет вид:
или
Решением данного уравнения Шредингера будет следующее выражение:
где k — волновое число, α — начальное значение координаты.
Т. о., полное решение уравнения (7) примет вид:
Это решение может быть представлено образом, приведённым на рисунке 2.
|
Рисунок 2 — Решение уравнения Шредингера для одномерной потенциальной ямы. |
Теперь
необходимо произвести сшивание
пси-функций в точках:
.
Для этого найдём условия непрерывности
для пси-функций, а именно необходимо,
чтобы выполнялись следующие равенства:
Выражение (11) равносильно, с учётом (10), выражению:
Из
первого равенства получаем, что
,
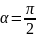поэтому:
Подставим полученное выражение (13) для волновой функции во второе уравнение, получим:
А
это условие выполняется, если
и из выражения
имеем, что:
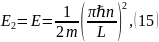
т. е. мы получили выражения для определения энергии электрона для любого значения главного квантового числа n. Тогда разница энергий при двух значениях n и m квантовых уровней будет иметь вид:
График для задания 1) приведён на рисунке 3.
|
Рисунок 3 — График функции
|
Все используем значения для вычислений приведены в таблице 2.
Таблица 2 — Дополнительные данные
Величина |
Значение |
Масса электрона [кг] |
9,10∙10−31 |
Постоянная Дирака [м2∙кг/с] |
1,05∙10−34 |
Диапазон: для задания 2) [м] |
−0,25∙10−9—0,75∙10−9 |
Диапазон n для задания 2) |
1—6 |
Вычисления и построение графиков будут проводиться в MATLAB. Код программы будет приведён в ПРИЛОЖЕНИИ А.
Продолжим сшивание пси-функции. Из выражения выразим k, получим:
Подставим его в (14), получим:
Для таких функций с различными целыми значениями n условие непрерывности выполняется.
Осталось только определить нормировочный коэффициент A. Это можно сделать, если обратиться к свойству пси-функции, одно из которых гласит, что:
Проделав интегрирование (19) и учтя, что нас интересуют только пределы интегрирования от 0 до L, получим:
Т. о., полное решение уравнения (7), с учётом сшивки пси-функций, будет иметь вид:
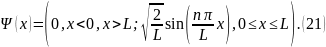
Построим теперь графики и . Графики соответствующих функций приведены на рисунках 4 и 5. (Код программы, с помощью которой были продела вычисления и построения графиков, приведён в ПРИЛОЖЕНИИ А.)
|
Рисунок 4 — График функции |
|
Рисунок 5 — График функции |
Вывод
В ходе выполнения работы была решена задача нахождения вида пси-функции электрона, находящегося в одномерной потенциальной яме с бесконечными стенками, посредством решения одномерного стационарного уравнения Шредингера. Было произведено сшивание пси-функции в граничных точка потенциальной ямы.
Были построены:
• график зависимости разности энергий двух квантовых уровней от ширины потенциальной ямы;
• график зависимости пси-функции от координаты электрона;
• график зависимости вероятности обнаружения электрона от координаты электрона.
ПРИЛОЖЕНИЕ А
Код программы MATLAB необходимый для построения графиков:
%расчёт для задания 1)
clear;
L1=0.5*(10^-9);
L2=5*(10^-9);
dL=0.04*(10^-9);
L=L1:dL:L2;
me=9.10*(10^-31);
h=1.05*(10^-34);
n=2;
m=1;
for i=1:113
E(i)=(1/(2*me))*(((pi*h)/(L(i)))^2)*(n^2-m^2);
end
plot(L,E,'black','Linewidth',2);
xlabel('L [м]','FontSize',14,'FontName','Times New Roman');
ylabel('∆_{E_m}E_n(L) [Дж]','FontSize',14,'FontName','Times New Roman');
%расчёт для задания 2)
clear;
%задание параметров и дискретизация величин
x1=-0.25*(10^-9);
x2=0.75*(10^-9);
dx=0.004*(10^-9);
x=x1:dx:x2;
n=1:1:6;
L=0.5*(10^-9);
Psi=zeros(length(x),length(n));
PSI=zeros(length(x),length(n));
%вычисление значений пси-функций и вероятностей
for j=1:6
for i=1:251
if x(i)<0
Psi(i,j)=0;
PSI(i,j)=0;
elseif x(i)>L
Psi(i,j)=0;
PSI(i,j)=0;
else
Psi(i,j)=sqrt(2/L)*sin((n(j)*pi*x(i))/L);
PSI(i,j)=abs(Psi(i,j))^2;
end
end
end
%графики Ψ-функций
f1=figure;
for j=1:6
subplot(2,3,j)
plot(x,Psi(:,j),'black','Linewidth',2);
title('n=','FontSize',14,'FontName','Times New Roman');
xlabel('x [м]','FontSize',14,'FontName','Times New Roman');
ylabel('Ψ','FontSize',14,'FontName','Times New Roman');
end
%графики вероятностей
f2=figure;
for j=1:6
subplot(2,3,j)
plot(x,PSI(:,j),'black','Linewidth',2);
title('n=','FontSize',14,'FontName','Times New Roman');
xlabel('x [м]','FontSize',14,'FontName','Times New Roman');
ylabel('Ψ^2','FontSize',14,'FontName','Times New Roman');
end
Таганрог 2022