Лабы / lab6

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №6

по дисциплине ТАУ

Тема: Метод гармонического баланса

Студентки гр. 0392		Алексеева Е.А.
		Кошмухамбетова Д.В.
		Сидорина Д.А.
Преподаватель		Жеронкин К. М.

Санкт-Петербург

2023

Цель работы.

Применение на практике метода гармонического баланса.

Основные теоретические положения.

Автоколебания — периодические процессы в автономных системах — практически важные режимы функционирования многих систем автоматического управления и регулирования. Если положение равновесия системы неустойчиво, то колебания реальной системы в силу естественных ограничений расходятся до определенной амплитуды.

Автоколебательные системы успешно применяются для поддержания различных физических переменных технологических процессов, если ыамплитуда и частота колебаний находятся в допустимых пределах. Релейная система стабилизация температуры, в которой наблюдаются автоколебания рассматривается в Лабораторной работе 2.

Точное определение формы и параметров периодических режимов возможно только для некоторых типов нелинейных систем, в частности релейных. Для исследования предельных циклов в системах второго порядка весьма удобен метод фазовой плоскости. На фазовой плоскости автоколебаниям отвечают устойчивые предельные циклы — изолированные замкнутые фазовые траектории (см. Лабораторную работу 3).

Во многих случаях системы управления описываются моделями высоких порядков и имеют сложные характеристики нелинейных элементов. В этих случаях применяют приближенные методы исследования периодических режимов. Важную информацию о существовании периодических режимов в нелинейных системах, их числе и параметрах может дать приближенный метод гармонического баланса. По результатам, полученным этим методом, могут быть оценены начальные условия для моделирования систем на ЭВМ с целью последующего уточнения форм и параметров локализованных периодических режимов. Расчетная структура нелинейных моделей изображена на рис. 6.1.

Рис. 6.1. Расчетная структура нелинейных моделей

Если СХ НЭ представляет нечетную функцию, то при отсутствии воздействия (f ≡ 0) в системе могут возникать симметричные автоколебания.

В методе гармонического баланса принимается гипотеза о форме искомого периодического процесса на входе НЭ (см. рис. 6.1). Параметризация решения принципиально упрощает задачу — ищется амплитуда A и частота ω решения.

Анализ включает этапы:

- гармоническая линеаризация НЭ;

- локализация параметров периодических решений по гармонически линеаризованной системе;

- анализ устойчивости предельного цикла.

Выполнение работы.

Задание 1. Исследуем автоколебания системы регулирования температуры, в которой роль регулятора играет реле с гистерезисом.

ЛЧ имеет ПФ:

1 этап. Гармоническая линеаризация НЭ.

Допустим, что А>b, тогда получим:

Эквивалентная передаточная функция имеет вид:

2 этап. Локализация параметров периодических решений по гармонически линеаризованной системе.

Используем методику Л.С. Гольдфарба. Графическая методика поиска параметров основана на условии

где: — амплитудно-фазовая характеристика ЛЧ, — инверсная характеристика НЭ. Точка их пересечения отвечает границе устойчивости эквивалентной системы. Частота колебаний локализуется по меткам на АФХ , а амплитуда — по меткам на инверсной характеристике .

Инверсная характеристика реле с гистерезисом выражается так:

Поскольку мнимая часть постоянна и не зависит от A, график этой характеристики есть прямая в третьем квадранте, параллельная оси абсцисс.

Построим частотную характеристику средствами Python библиотеки control или средствами MatLab:

A = 4.05 C = 5 b = 0.5 l = np.sqrt(A*A - b*b) w_l = control.tf([1], [1, 2, 1, 0]) w_n = control.tf([ complex(-np.pi*l, -np.pi*b)], [4*C]) plt.axhline( -np.pi*b/(4*C), color='r') plt.axvline( -np.pi*l/(4*C),color='g') control.nyquist(w_l) plt.legend(['pi*sqrt(A*A - b*b)/(4*C)','pi*b/(4*C)','W(wj)']) plt.ylim(-0.5, 0.5) plt.xlim(-1, 0.1) plt.plot() plt.show()

Рис. 6.3. Иллюстрация методики Гольдфарба.

Получили А=4.05 и w=0.88. Эта частота меньше, чем у идеального реле, что и понятно, ведь реле с гистерезисом вносит отрицательный фазовый сдвиг.

3 этап. Анализ устойчивости периодического решения.

Методика Л.С. Гольдфарба оперирует годографами на комплексной плоскости. Точки инверсной характеристики НЭ при конкретных значениях амплитуды A играют роль критических точек в формулировке критерия Найквиста. При проходит через критическую точку — гармонически линеаризованная система находится на колебательной границе устойчивости.

Если возмущения привели к изменению амплитуды , то могут быть две ситуации.

Увеличение амплитуды приводит к тому, что АФХ ЛЧ не охватывает критическую точку (см. рис 6.4)— система устойчива, колебания затухают до прежнего значения.

Рис. 6.4.

При уменьшении амплитуды АФХ ЛЧ охватывает критическую точку , а значит, система не устойчива, колебания расходятся. Вывод — периодическое решение устойчиво.

Рис. 6.5.

Задание 2. Полученные методом гармонического баланса результаты анализа автоколебаний сравним с результатами компьютерной имитации.

Рис. 6.6. Scope сигнала, прошедшего через систему

Видим, что А=4.05 и T=7.3, откуда w=0.87. Это схоже с тем, что мы получили при методе гармонического баланса.

Задание 3. Анализ спектра сигналов в нелинейной системе. Проанализируем условия прохождения гармонического сигнала по контуру, образованному НЭ, ЛЧ и элементом сравнения. Допустим, что несмещенный сигнал на выходе НЭ

имеет ту же частоту (тот же период T = 2π/ω), что и вход. В силу нелинейного характера преобразования y = F(x) сигнал y(t), кроме первой гармоники, содержит и высшие гармоники. НЭ выступает как генератор высших гармоник.

Пусть линейная часть системы с передаточной функцией W (s) является фильтром низких частот (гипотеза фильтра). Проходя через ЛЧ, высшие гармоники ослабляются в большей степени, чем первая гармоническая составляющая. Поэтому в составе переменной на выходе ЛЧ доля высших гармоник мала:

Рис. 6.7. ЛАЧХ и ЛФЧХ ЛЧ

На рис. 6.7 приведена амплитудно-частотная характеристика ЛЧ. Можно видеть, что теоретические значения при равны:

Проведем анализ спектров колебаний на входе и выходе ЛЧ, т. е. на выходе и входе реле с гистерезисом. Сигнал на выходе реле и входе ЛЧ — меандр; известно, что он содержит только нечетные гармоники с амплитудами: и т. д.

Построим спектры на входе и выходе ЛЧ. Сигнал на входе НЭ это сигнал на выходе ЛЧ и наоборот, так как обратная связь их связывает.

Рис. 6.8. Спектр сигнала на входе ЛЧ

Рис. 6.9. Спектр сигнала на выходе ЛЧ

Видим, что НЭ порождает высшие гармоники (см. рис. 6.9), то есть на. А вот ЛЧ представляет собой ФНЧ и оставляет только первую гармонику с частотой w=0.00013 кГц.

Оценим влияние НЭ на спектральные характеристики системы.

Рис. 6.10. Спектр сигнала системы с НЭ

Рис. 6.11. Спектр сигнала системы без НЭ

Видим, что НЭ дает энергию гармоникам, откуда в большей степени увеличивается амплитуда гармоник, которые меньше первой. Сигнал становится шумнее.

Проведем эксперименты и посмотрим, как спектральные характеристики реле с гистерезисом зависят от амплитуды и частоты входного сигнала.

Рис. 6.12. Спектр сигнала A =4, w = 0,88 до/после НЭ.

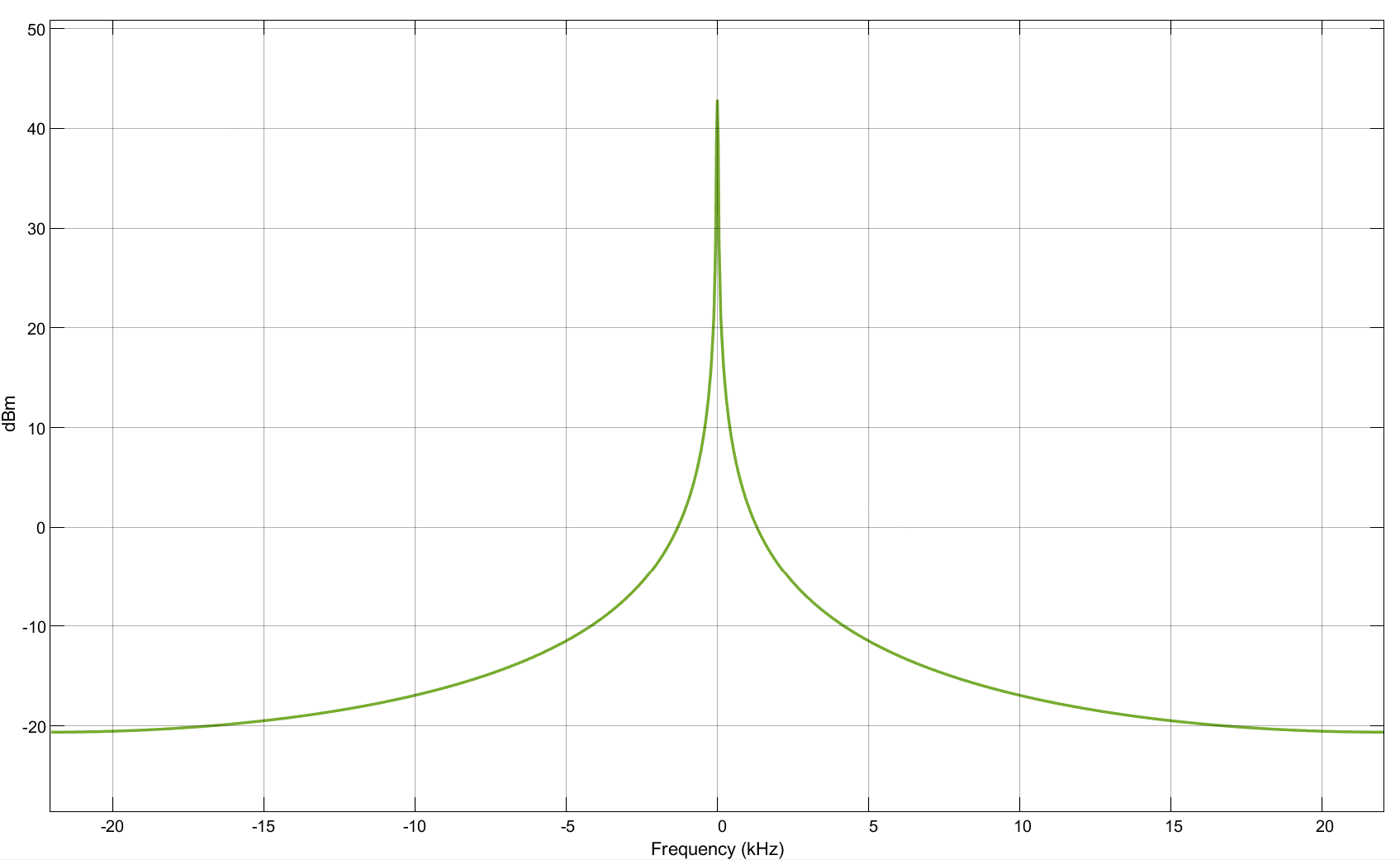
Рис. 6.13. Спектр сигнала A = 50, w = 0,88 до/после НЭ.

Рис. 6.14. Спектр сигнала A = 0.7, w = 0,88 до/после НЭ.

Видим, что с увеличением/уменьшением амплитуды сигнала соразмерно увеличивается/уменьшается и амплитуды спектра соответственно.

Рис. 6.15. Спектр сигнала A = 4, w = 0.1 до/после НЭ.

Рис. 6.16. Спектр сигнала A = 4, w = 10 до/после НЭ.

С увеличением частоты сигнала появляются лепестки, ширина спектра увеличивается.

Вывод.

Параметры автоколебаний, найденные экспериментально, достаточно точно совпадают с теоретическими. Чем ближе начальное значение системы к амплитуде автоколебаний, тем быстрее они устанавливаются.