Лабы / lab5

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №5

по дисциплине ТАУ

Тема: Анализ устойчивости положения равновесия

Студентки гр. 0392		Алексеева Е.А.
		Кошмухамбетова Д.В.
		Сидорина Д.А.
Преподаватель		Жеронкин К. М.

Санкт-Петербург

2023

Цель работы.

Анализ устойчивости нелинейных систем методами Ляпунова.

Основные теоретические положения.

Первый метод Ляпунова позволяет судить об устойчивости изолированного положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:

- если собственные значения (с.з.) линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;

- если среди с.з. линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;

- если имеются некратные с.з. на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

Выполнение работы.

Задание 1. Проанализируем первым методом Ляпунова нелинейный осциллятор, заданный системой дифференциальных уравнений.

Найдем координаты положения равновесия: из условий . У системы единственное положение равновесия в точке (0, 0). Исследуем устойчивость положение равновесия с помощью первого метода Ляпунова.

Запишем матрицу состояний линеаризованной системы:

Вычислим ее собственные значения, предварительно записав Х.П. матрицы:

Получили, что матрица системы имеет мнимые собственные значения , т.е. линеаризованная система находится на границе устойчивости. Критическая точка типа центр. В данном случае нельзя судить об устойчивости положения равновесия нелинейной системы. Обратимся ко второму методу Ляпунова.

Для устойчивости нам достаточно существования положительно - определённой функции, полная производная по времени которой является отрицательно - определенной

Выберем скалярную функцию переменных состояний в виде квадратичной формы:

и продифференцируем её по времени:

Получили отрицательно-определённую функцию, что означает асимптотическую устойчивость положения равновесия. Поскольку при имеем , то положение равновесия устойчиво в целом.

Отметим, что с приближением к началу координат относительное затухание процессов уменьшается, т.к. ослабляется влияние нелинейного демпфирующего члена .

Рис.1 Фазовый портрет осциллятора

Задание 2.

Проанализируем первым методом Ляпунова систему, заданную структурной схемой:

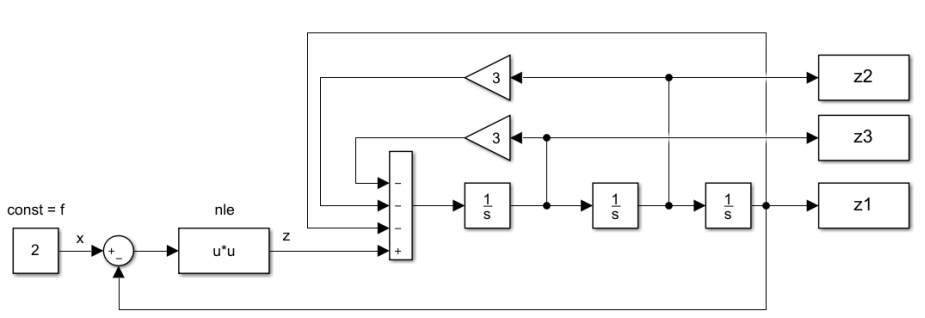
Рис. 2 Структура модели

Система ДУ данной системы:

У системы два положения равновесия в точках (1, 0, 0) и (4, 0, 0). Запишем матрицу состояний линеаризованной системы:

Х.П. матрицы в (1, 0, 0): .

Корни:

устойчивое положение равновесия

Х.П. матрицы в (4, 0, 0): .

Корни:

неустойчивое положение равновесия

Система устойчива «в малом».

Рис. 3-4 Фазовый портрет системы

Вывод.

Был произведен анализ устойчивости двух нелинейных систем первым и вторым методом Ляпунова.