
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчет
по лабораторной работе №4
по дисциплине «Теория автоматического управления»
Тема: Метод фазового пространства
Студентки гр.0392 |
|
Алексеева Е.А. Кошмухамбетова Д.В. Сидорина Д.А. |
Преподаватель |
|
Жеронкин К.М. |
Санкт-Петербург
2023
Цель работы.
Анализ поведения систем с помощью метода фазового пространства.
Основные теоретические положения.
Хотя геометрическая интерпретация метода пространства состояний распространяется на системы любого порядка, важное его преимущество — наглядность — наиболее ярко проявляется в случае систем второго порядка, когда состояния системы представляются точками на фазовой плоскости. Следует добавить, что нелинейные модели второго порядка позволяют выявлять многие принципиальные особенности поведения динамических систем; это определяет методическое, теоретическое и практическое значение метода фазовой плоскости. Метод фазовой плоскости дает возможность изобразить качественную картину всей совокупности свободных движений (процессов) для выбранной области начальных условий (состояний), а при необходимости – провести исследования типов движений. Через каждую точку фазового пространства при условии однозначности функции проходит только одна фазовая траектория. Единственность нарушается в особых точках, отвечающих точкам равновесия.
На фазовой плоскости существует несколько основных типов особых точек (типов поведения в окрестности положения равновесия):
устойчивый узел (корни ХП – действительные числа, оба знака "-");
неустойчивый узел (корни ХП – действительные числа, оба знака "+");
седло (корни ХП – действительные числа, разного знака);
устойчивый фокус (корни ХП – комплексные числа, действительные части которых равны, отличны от нуля, знака "-");
неустойчивый фокус (корни ХП – комплексные числа, действительные части которых равны, отличны от нуля, знака "+");;
центр (корни ХП – чисто мнимые числа (действительная часть равна 0));.
Особые точки являются частным случаем аттракторов (от англ. to attract — притягивать) — компактных подмножеств фазового пространства динамической системы, к которым стремятся все траектории из некоторой окрестности. Аттракторами могут быть замкнутые траектории (предельные циклы) или ограниченные области с неустойчивыми траекториями внутри (как у «странного» аттрактора).
Обработка результатов эксперимента
Построение фазовых портретов для типовых особых точек
Построим фазовые портреты систем для анализа поведения решений в окрестности особых точек, используя Jupiter Notebook на языке Python.
Устойчивый узел

Рисунок 1 – Фазовый портрет устойчивого узла
def ode(Y, t, b): x, y = Y dydt = [-4*x-4*y, 1.5*x+y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 2, nt = 301)
Все линии фазовой траектории такой системы стремятся в начало координат (0, 0), особую точку. Собственные числа – действительные отрицательные, следовательно, такая система устойчива. Прямолинейным фазовым траекториям соответствуют состояния, когда постоянные при одной из экспонент равняются нулю.
Неустойчивый узел

Рисунок 2 – Фазовый портрет неустойчивого узла
def ode(Y, t, b): x, y = Y dydt = [x+0.5*y, 0.5*x+y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 2, nt = 301)
Все линии фазовой траектории такой системы отдаляются от начала координат (0, 0), никогда его не проходят. При положительных действительных корнях имеем особую точку типа "неустойчивый узел", следовательно, такая система неустойчива.
Седло

Рисунок 3 – Фазовый портрет седла
def ode(Y, t, b): x, y = Y dydt = [2*x+y, x-3*y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 0.5, nt = 301)
Как и в случае с "неустойчивым узлом" фазовый портрет "седла" не имеет пересечений центра координат (0;0). Имеются прямолинейные траектории – сепаратрисы (сепаратриса – кривая, которая начинается или заканчивается в точке седлового состояния равновесия) седла, которые соответствуют случаю, когда один из коэффициентов характеристического полинома равен нулю. У седла 4 сепаратрисы: 2 устойчивые (направлены к седловой точке) и 2 неустойчивые (направлены от седловой точки). Такая особая точка получается, когда корни полинома разных знаков. Система неустойчива.
.
Устойчивый фокус

Рисунок 4 – Фазовый портрет устойчивого фокуса
def ode(Y, t, b): x, y = Y dydt = [2*y, -3*x-y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 2, nt = 301)
На рисунке запечатлены закругленные линии фазовых траекторий, которые стремятся к центру системы координат, спирали. Такое положение линий сохраняется, если имеются комплексно-сопряженные корни с отрицательными действительными частями. Система устойчива.
Неустойчивый фокус

Рисунок 5 – Фазовый портрет неустойчивого фокуса
def ode(Y, t, b): x, y = Y dydt = [0.1*x-4*y, 4*x+0.1*y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 1, nt = 301)
Фазовые траектории представляют собой спирали. Если действительные части комплексных корней положительны, то имеем "неустойчивый фокус" и колебательные расходящиеся процессы. Система неустойчива
Центр

Рисунок 6 – Фазовый портрет центра
def ode(Y, t, b): x, y = Y dydt = [x-4*y, 2*x-y] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 2, nt = 301)
На рисунке представлен незатухающий колебательный процесс. Здесь можно наблюдать замкнутые, вложенные друг в друга, эллипсы с увеличивающимся радиусом, и отсутствие пересечений координатного центра. Система находится на границе устойчивости.
Построение фазового портрета для маятника.
def ode(y, t, c): theta, omega = y dydt = [omega, – c*np.sin(theta)] return dydt c = 0.29 # Параметр ОДУ (длина маятника) args=(c, ) drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 8 nt =301)

Рисунок 7 – фазовый портрет математического маятника
Рисунок демонстрирует движение математического маятника. Здесь мы можем рассмотреть два типа особых точек. В точках (2*pi*k, 0) k = 0, +- 1, ... маятник направлен вертикально вниз, в этот момент времени имеются замкнутые линии фазовых траекторий. На данном участке времени отмечается максимальная скорость его прохождения. Этому положению равновесия отвечает особая точка типа "центр", следовательно, характеристический полином имеет пару мнимых корней. А на верхних участках вращательного движения вокруг точки подвеса (pi*(k - 1), 0) k = +- 1, ... скорость маятника уменьшается, что демонстрируют незамкнутые траектории. Они, также, являются границами областей с колебательным движением. Характеристический полином для верхних положений равновесия имеет действительные корни разных знаков; этим положениям равновесия отвечает особая точка типа "седло". Такое положение равновесия не назовешь устойчивым, т.к. малейшее отклонение приведет к колебательному движению.Сепаратрисы – границы областей между колебательными движениями и незамкнутыми траекториями вне этих областей, изображающими неравномерные вращательные движения маятника вокруг точки подвеса.
Фазовый портрет маятника с учетом вязкого трения
m = 0.2 * 17 l = 5 / 17 b = 0.1 + 0.015*17 def ode(y, t, b): theta, omega = y dydt = [omega, -b * omega – m*9.81*l*np.sin(theta)] return dydt args=(c, ) drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 4, nt =301)

Рисунок 8 – фазовый портрет математического маятника с учетом вязкого трения
Модель математического маятника на рисунке стремится к устойчивому положению равновесия из-за наличия вязкого трения. Модель внешне похожа на особую точку типа "устойчивый фокус". Отражается колебательный процесс с затуханием. Это подтверждается отсутствием замкнутых фазовых траекторий. Следовательно, в характеристическом полиноме имеются комплексно-сопряженные корни с отрицательными действительными частями. По мере удаления от особой точки фазовый портрет нелинейной системы может иметь существенные отличия.
Построение фазовых портретов для нелинейных систем

Рисунок 9 – Структурная схема системы
Составим систему ДУ по структурной схеме:

b = 0.2*17 + 0.2 def dead_zone_scalar(x, width=b): if np.abs(x) < width: return 0 elif x > 0: return x – width else: return x + width dead_zone = np.vectorize(dead_zone_scalar, otypes=[np.float], excluded=['width'])
def ode(Y, t, b): x,y = Y dydt = [y, -y - np.sign(dead_zone(x, 0.2 * 17 + 0.2))] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 100, nt =301)

Рисунок 10 – Фазовый портрет нелинейной системы
Видим, что процесс разбит на ряд интервалов (из-за переключения релейного элемента). На фазовой плоскости каждому линейному участку такой характеристики НЭ соответствует отдельная область, где правые части ДУ линейны, а фазовые траектории состоят из дуг траекторий линейной системы. В случае нелинейной системы можно сразу найти положения равновесия: y = 0 как вход интегратора в равновесном состоянии; |x| <= b, |y| <= b, где b - амплитуда мертвой зоны. Те на промежутке имеет место отрезок равновесия. В данном случае он x = +-3.6. Линии соответствуют границы трех листов фазовой плоскости. Движения системы завершаются на отрезке равновесия. Фазовый портрет данной системы имеет особую точку типа "Устойчивый узел". У данной системы отрицательные действительные корни. Положение равновесия устойчиво.
Построение фазового портрета осциллятора Ван дер Поля
Дифференциальные уравнения генератора колебаний (осциллятора) предложены голландским инженером и физиком Бальтазаром ван дер Полем. Им были найдены устойчивые колебания, которые были названы релаксационными, известные как «предельные циклы». Уравнение Ван дер Поля применяется в физике и других областях науки и техники. Оно также 34 было использовано в сейсмологии для моделирования геологических разломов. Например, в биологии создана модель Фитц Хью-Нагумо.

У осциллятора Ван дер Поля есть несколько режимов: при μ = 0 и при μ > 0. Чем дальше μ от нуля, тем колебания осциллятора более похожи на гармонические.
var = 17 def ode(Y, t, b): x, y = Y dydt = [y, var * (1 - x * x) * y - x ] return dydt drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 1, nt =301)

Рисунок 11 - Фазовый портрет осциллятора Ван дер Поля при μ = 17.
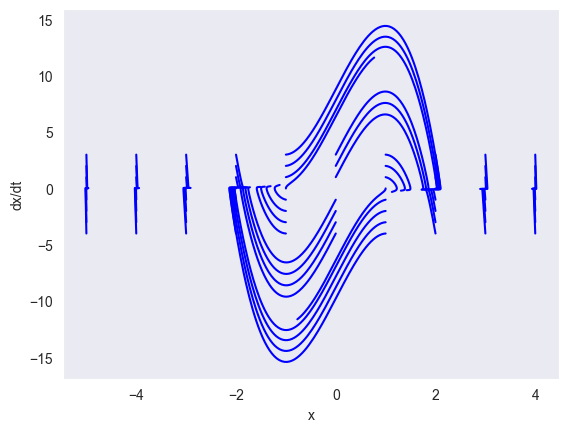
Рисунок 12 - Фазовый портрет осциллятора Ван дер Поля при μ = 17/2.

Рисунок 13 - Фазовый портрет осциллятора Ван дер Поля при μ = 17*2.
На рисунках в центре изображен предельный цикл. Он устойчив, это означает, что ему отвечают автоколебания в системе, независящие от начальных условий, определяющиеся свойствами самой системы. При изменении μ автоколебания не пропадают. Чем больше μ, тем колебания осциллятора более похожи на гармонические. Чем больше μ, тем больше амплитуда.
Построение фазового портрета аттрактора Лоренца (3 порядок)
Аттрактор Лоренца (от англ. to attract притягивать) компактное инвариантное множество L в трехмерном фазовом пространстве гладкого потока, которое имеет определенную сложную топологическую структуру и является асимптотически устойчивым. Он устойчив по Ляпунову - все траектории из некоторой окрестности L стремятся к L при t → ∞ (отсюда название).
Система дифференциальных уравнений Лоренца записывается так:
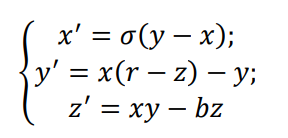
для параметров: σ = 10, r = 28, b = 8/3 и начальных условий x(0) = 1, y(0) = 0, z(0) = 0.
def ode(y, t, sigma, r, b): x,y,z = y dxdt = sigma * (y-x) dydt = x * (r - z) – y dzdt = x*y – b*z return [dxdt, dydt, dzdt] # реализуем функцию, реализующую запуск вычисления ОДУ def calcODE(args, x, y, z, ts = 10, nt = 101): y0 = [x, y, z] t = np.linspace(0, ts, nt) sol = odeint(ode, y0, t, args) return sol # реализуем функцию, реализующую расчет и рендер 3D фазового #портрета и его проекций def drawPhasePortrait3D(args, deltaX=1, deltaY=1, deltaZ=1, startX=0, stopX=5, startY=0, stopY=5, startZ=0, stopZ=5, ts=10, nt=101): fig = plt.figure() ax = fig.add_subplot(2, 2, 1, projection='3d') ax.set_title("3D") plt.subplot(2, 2, 2) plt.title("X-Y") plt.grid() plt.subplot(2, 2, 3) plt.title("X-Z") plt.grid() plt.subplot(2, 2, 4) plt.title("Y-Z") plt.grid() for x in range(startX, stopX, deltaX): for y in range(startY, stopY, deltaY): for z in range(startZ, stopZ, deltaZ): sol = calcODE(args, x, y, z, ts, nt) ax.plot(sol[:, 0], sol[:, 1], sol[:, 2]) plt.subplot(2, 2, 2) plt.plot(sol[:, 0], sol[:, 1]) plt.subplot(2, 2, 3) plt.plot(sol[:, 0], sol[:, 2]) plt.subplot(2, 2, 4) plt.plot(sol[:, 1], sol[:, 2]) plt.show()
sigma = 10 r = 0.1 b = 8 / 3 args = (sigma, r, b) drawPhasePortrait3D(args, deltaX=4, deltaY=4, deltaZ=4, startX=-10, stopX=10, startY=-10, stopY=10, startZ=-10, stopZ=10, ts=10, nt=1001)

Рисунок 14 - Аттрактор Лоренца при r = 0.1.

Рисунок 15 - Аттрактор Лоренца при r = 28

Рисунок 16 - Аттрактор Лоренца при r = 100
Можно увидеть две неустойчивые траектории, исходящие из начала координат, совершив полный оборот вокруг одной из устойчивых точек,возвращаются в начало координат при t → ∞. Фазовые траектории спирально приближаются к двум критическим точкам, что соответствует наличию затухающих колебаний.
На рисунках 14-16 построены фазовые портреты аттрактора Лоренца. При r<1 аттрактором является начало координат, других устойчивых точек нет. При r>1,а именно r=28 имеются 2 аттрактора - локальный и глобальный. Фазовые траектории делают несколько оборотов то вокруг одной неустойчивой стационарной точки, то вокруг другой, меняя их. Также некоторые фазовые траектории около точек представляют собой неустойчивые предельные циклы, а другие направленно приближаются к ним. При увеличении радиуса система переходит в режим автоколебаний, траектория претерпевает серьезные изменения.В зависимости от направления траектория приходит в одну из двух устойчивых точек.
Типовые фазовые портреты
Система 1
def ode(Y, t, n):
x,y = Y
dydt = [ -4*x + 0.1*n*(x**2) - 4*y, 1.5*x + y - 0.2*n*(y**3) ]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x,y = Y
dydt = [ -4*x - 4*y, 1.5*x + y ]
return dydt


Рис. 15 Фазовые портреты системы 1 (нелинеаризованной и линеаризованной)
Фазовые портрет системы после линеаризации сильно изменился. Фазовый портрет имеет вид особой точки "Устойчивый узел". Система имеет отрицательные вещественные корни. Положение равновесия устойчиво.
Система 2
def ode(Y, t, n):
x, y = Y
dydt = [ x + 0.5*y - 0.1 * n * (y**2), 0.5*x + y - 0.2*n*(y**3)]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x, y = Y
dydt = [ x + 0.5*y, 0.5*x + y]
return dydt


Рис. 16 Фазовые портреты системы 2 (нелинеаризованной и линеаризованной)
Фазовый портрет имеет вид особой точки "Неустойчивый узел". Фазовый портрет линеаризованной системы сильно отличается от первоначальной. По фазовому портрету можно понять, что все фазовые траектории данной системы стремятся от единственной точки равновесия. Система неустойчива, имеет положительные действительные корни.
Система 3
def ode(Y, t, n):
x, y = Y
dydt = [ 2*x + 0.2 * n * (x**2) + y - 0.1* n *(y**2), x - 3*y ]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x, y = Y
dydt = [ 2*x + y, x - 3*y ]
return dydt


Рис. 17 Фазовые портреты системы 3 (нелинеаризованной и линеаризованной)
Фазовый портрет имеет вид особой точки "Седло". Система имеет положительные и отрицательные корни. Фазовый портрет линеаризованной системы практически не отличается от первоначальной. Положение равновесия неустойчиво.
Система 4
def ode(Y, t, n):
x, y = Y
dydt = [ -0.1 * n *(x**2) + 2*y, -3*x - y ]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x, y = Y
dydt = [ 2*y, -3*x - y ]
return dydt


Рис. 18 Фазовые портреты системы 4 (нелинеаризованной и линеаризованной)
Фазовый портрет имеет вид особой точки "Устойчивый фокус". Система имеет комплексно-сопряженные корни с отрицательными действительными частями. Фазовый портрет линеаризованной модели практически не отличается от первоначальной. Система является устойчивой.
Система 5
def ode(Y, t, n):
x, y = Y
dydt = [ 0.1*x - 4*y, 4*x - 0.2 * n *(x** 2) + 0.1*y ]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x, y = Y
dydt = [ 0.1*x - 4*y, 4*x + 0.1*y ]
return dydt
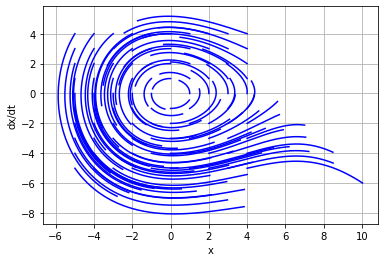

Рис. 19 Фазовые портреты системы 5 (нелинеаризованной и линеаризованной)
В данной системе фазовые траектории расходятся от центра, а собственные числа матрицы состояний комплексно-сопряженные и находятся в правой полуплоскости. Такая система неустойчива.
Система 6
def ode(Y, t, n):
x, y = Y
dydt = [ x - 0.1 * n *(x** 2) - 4*y + 0.3 * n *(y** 2), 2*x + 0.2 * n *(x ** 2) - y - 0.3 * n *(y**3) ]
return dydt
В случае линеаризованной системы:
def ode(Y, t, n):
x, y = Y
dydt = [ x - 4*y, 2*x - y ]
return dydt


Рис. 20 Фазовые портреты системы 6 (нелинеаризованной и линеаризованной)
Можно заметить, что фазовые траектории не приближаются и не отдаляются от центра. Собственные числа комплексно-сопряженные и находятся на мнимой оси. Такая система находится на колебательной границе устойчивости.
Выводы.
В данной лабораторной работе было произведено знакомство с методами фазового пространства. Были построены и проанализированы особые точки фазового пространства, фазовый портрет математического маятника с учетом вязкого трения и без, фазовый портрет нелинейной системы, а также, фазовые портреты осциллятора Ван Дер Поля и аттрактора Лоренца с различными параметрами. Был построен фазовый портрет системы, заданной в виде структурной схемы.
