Курсовая / Отчет по курсовику

МИНОБРНАУКИ РФ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)

Факультет компьютерных технологий и информатики Кафедра автоматики и процессов управления

СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПЕРЕВЕРНУТЫМ МАЯТНИКОМ НА КАРЕТКЕ

Пояснительная записка к курсовому проектированию по дисциплине «Теория автоматического управления»

Санкт-Петербург

2023

4. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ОПЕРАТОРНЫМ МЕТОДОМ26

4.1. Операторный метод размещения корней характеристического полинома

4.2. Пример стабилизации перевернутого маятника на закрепленной каретке. 28

5. СИНТЕЗ СИСТЕМЫ СТАБИЛИЗАЦИИ ЧАСТОТНЫМ МЕТОДОМ.. 37

. 6. СИСТЕМЫ С ЦИФРОВЫМИ УПРАВЛЯЮЩИМИ УСТРОЙСТВАМИ

48

2

ПРЕДИСЛОВИЕ

Динамические модели перевернутых маятников различной конфигурации используются в научных публикациях для сравнения методов синтеза алгоритмов автоматической стабилизации, а также в учебном процессе технических университетов в качестве наглядных примеров неустойчивых объектов.

Отмечается, что многозвенные перевернутые маятники служат примерами шагающих роботов, ракет на старте, нескольких барж, которых толкает буксир и т. д. и т. п.

Целью курсового проектирования является освоение методов моделирования, анализа и синтеза систем автоматического управления с помощью современных инструментальных средств.

Для достижения цели необходимо решить следующие задачи:

-построить нелинейную математическую модель объекта управления;

-провести анализ объекта методом компьютерной имитации;

-провести анализ устойчивости, управляемости и наблюдаемости объекта по линеаризованной модели;

-синтезировать регуляторы методом пространства состояний;

-синтезировать регуляторы частотным методом;

-провести анализ нелинейных систем управления;

-выбрать алгоритмы цифрового управления непрерывным объектом.

3

1. ПЕРЕВЕРНУТЫЙ МАЯТНИК НА КАРЕТКЕ КАК ОБЪЕКТ УПРАВЛЕНИЯ

1.1. Перевернутый маятник на каретке

Принципиальная схема механического объекта — перевернутого маятника на каретке — изображена на рис. 1.1, где приняты следующие обозначения параметров:

●m – масса маятника, кг;

●M – масса каретки, кг;

●l – длина маятника, м,

атакже переменных:

●θ(t) – угол отклонения маятника, рад;

●x(t) – положение каретки, м;

●f(t) – сила, действующая на каретку, Н (кг*м/сек2).

Целью управления является стабилизация верхнего положения равновесия маятника.

Рис. 1.1. Принципиальная схема перевернутого маятника на каретке

Рассматриваемый объект имеет две степени свободы – вращательное движение маятника и поступательное движение каретки.

4

Управление таким объектом осложняется тем обстоятельством, что имеется только одно управляющее воздействие – сила f(t), приложенная к каретке.

1.2. Математическая модель объекта управления

Методы синтеза систем автоматического управления непрерывными объектами основаны на математических моделях в виде дифференциальных уравнений.

Рис. 1.1 можно интерпретировать как символьную модель, представленную на языке механики. Для перевода знаний с языка механики (рис. 1.1) на язык математических моделей используют законы классической механики. Такой способ построения математических моделей называют аналитическим — он возможен для объектов хорошо изученной природы.

Примем следующие допущения:

-массы маятника и каретки сосредоточены;

-отсутствует сопротивление среды и трение;

Вкачестве обобщенных координат для рассматриваемой системы с двумя степенями свободы выберем y(t) — угол отклонения маятника и x(t) — положение каретки.

Математическая модель рассматриваемого объекта в виде системы двух дифференциальных уравнений второго порядка имеет вид:

Уравнение (1.1) представляет собой выражение баланса моментов, действующих на маятник, а уравнение (1.2) — баланса сил, действующих на каретку.

5

1.3. Дифференциальные уравнения в форме Коши

Анализ объекта и его компьютерное моделирование упрощаются, если дифференциальные уравнения разрешены относительно старших производных.

Заметим, что вторые производные в уравнения (1.1), (1.2) входят линейно. С учетом этого, приведем систему уравнений к матричной форме:

Прежде всего, проверим существование и единственность решения — вычислим определитель матрицы:

= ( + ) − 2 = + 2 ≠ 0

и убедимся в том, что он не равен нулю.

Для решения системы уравнений воспользуемся правилом Крамера

Теперь легко записать уравнения объекта в форме Коши:

(1.3)

Заметим, что правые части уравнений не содержат переменных , т. е. положение и скорость каретки не влияют на ускорения маятника и

6

каретки. Объект может занимать любое положение или совершать равномерное поступательное движение.

2.АНАЛИЗ ОБЪЕКТА УПРАВЛЕНИЯ

2.1.Компьютерное моделирование

Исходные нелинейные дифференциальные уравнения (1.3) нельзя решить аналитическим способом. Поэтому используют численные решения при конкретных начальных условиях и внешних воздействиях. Для автоматизации численных решений разработаны программные средства; далее будем использовать программу MATLAB/Simulink фирмы

The MathWorks, Inc.

Построение компьютерной модели сводится к выбору соответствующих библиотечных блоков и их соединение ориентированными связями, как показано на рис. 2.1.

Рис. 2.1. Модель объекта на языке графического редактора Simulink

7

Представленная на рис. 2.1 схема — модель объекта (программа) на языке графического редактора Simulink. Основу программы образуют два двойных интегратора, входами которых являются вторые производные переменных. Блоки Fcn и Fcn1, реализуют выражения, находящиеся в правых частях второго и четвертого уравнений системы (1.3). На входы этих блоков подается вектор , сформированный блоком mux.

Выберем следующие значения параметров: l = 1 м; m = 0.1 кг; M = 0.5 кг.

Сохраним модель под именем ′pendulum′.

Проведем компьютерный эксперимент при начальных условиях: — маятник отклонен на 1 рад, угловая скорость маятника, положение и скорость каретки равны нулю. Рассматриваем свободные движения автономной системы — к каретке не приложена сила, т. е не оказывается управляющее воздействие f = 0.

На рис. 2.2 приведены результаты компьютерной имитации объекта. Из графиков ясно, что верхнее положение маятника не устойчиво — при отклонении от него состояние системы не возвращается к нему, а начинаются колебания маятника с амплитудой (π − 1) радиан относительно нижнего положения равновесия. Каретка также совершает периодические движения своеобразной формы (при движениях автономной механической системе центр тяжести остается неизменным).

Колебания маятника и каретки не затухают, так как математическая модель игнорирует потери энергии на преодоление сопротивления среды и трение.

Для стабилизации верхнего положения равновесия маятника необходимо создать автоматическую систему управления.

8

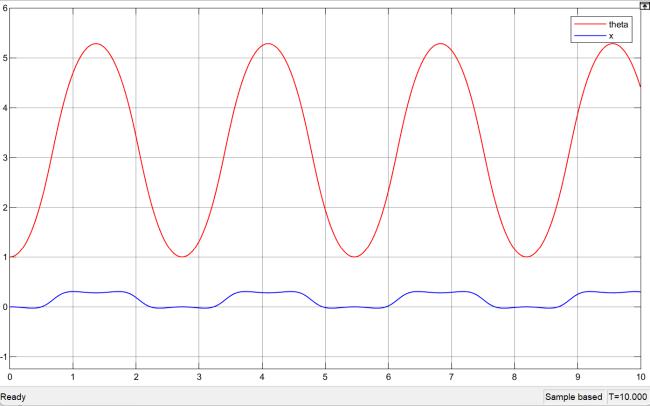
Рис. 2.2. Поведение объекта при начальных условиях — маятник отклонен на 1 радиан, а каретка не отклонена.

2.2. Линеаризация дифференциальных уравнений

Аналитические методы синтеза систем управления по нелинейным моделям разработаны только для частных случаев.

Анализ устойчивость «в малом» верхнего положения равновесия маятника можно выявить по линеаризованной модели. Ляпунов показал (первый метод), что об устойчивости «в малом» положении равновесия можно судить по линеаризованным уравнениям.

Будем рассматривать малые отклонения переменных и , когда приближенно можно принять:

Пренебрегая малыми величинами высших порядков, вместо нелинейных уравнений (1.3) получим линеаризованные уравнения в символьном виде:

9

;

(2.1)

Запишем линейную систему (2.1) в матричной форме с

использованием вектора состояний :

(2.2)

(2.3)

Первое из этих уравнений (2.2) называется уравнением состояний, второе (2.3) — уравнением выхода. В уравнении (2.3) за выход объекта — непосредственно измеряемую переменную — принято положение каретки, т. е. скаляр. Поэтому матрица выхода С оказывается строкой.

Получена линейная модель в так называемой форме пространства

Линеаризованные уравнения (2.1)—(2.4) позволяют исследовать устойчивость и процессы при малых отклонениях состояния маятника на каретке от верхнего положения равновесия.

10