Лекция 5

ЛЕКЦИЯ 5

КОНТАКТНАЯ ЗАДАЧА

Гибкие и жесткие фундаменты. Уравнение изогнутой оси фундамента. О моделях Фусса-Винклера и ТЛДС. Основное уравнение модели Фусса-Винклера.

Решение для жесткого фундамента по модели Фусса-Винклера. Основное уравнение модели ТЛДС. Решение для жесткого фундамента по модели ТЛДС.

5.1. Гибкие и жесткие фундаменты

С точки зрения реальной работы фундаментов граничные условия в задачах Мичелла и Лява-Короткина имеют один существенный недостаток. Он заключается в том, что, прикладывая нагрузку к основанию, мы получали криволинейное очертание поверхности в месте приложения нагрузки (см., например, рис. 3.11). Это имеет два важных взаимоувязанных следствия.

Во-первых, фундамент в этих решениях не только получал осадку, но еще и изгибался, причем изгиб полностью определялся деформацией основания, а в качестве осадки принимался или максимальный «прогиб» линии подошвы фундамента, или так называемая средняя осадка.

Во-вторых, такой «фундамент» передает на основание равномерно распределенное давление. В то же время в большом числе случаев давление по подошве реальных фундаментов распределяется неравномерно. Характер этого распределения определяется жесткостью фундаментов.

Таким образом, при моделировании НДС на контакте основания и фундамента можно выделить три способа передачи нагрузки в зависимости от жесткости фундаментов:

абсолютно гибкий фундамент, когда деформированный вид линии подошвы фундамента следует за деформациями основания, т.е. нагрузка как бы состоит из отдельных несвязанных между собой элементарных сил (рис. 5.1, а);

абсолютно жесткий фундамент, когда линия подошвы остается прямой после деформации (рис. 5.1, б);

фундамент конечной жесткости, когда линия подошвы деформируется, но величина деформации определяется конечным соотношением жесткостей основания и фундамента (рис. 5.1, в).

Различие в деформированных схемах, несомненно, повлечет за собой и несовпадение напряженного состояния, особенно в местах приложения давления.

В этой связи важно отметить следующее.

Согласно принципу Сен-Венана по мере удаления от места приложения нагрузки напряженное состояние все меньше зависит от способа передачи нагрузки на среду и определяется лишь величиной нагрузки. Поэтому приходим к важному выводу о корректности рассмотренных выше решений ТЛДС для задач определения напряженно-деформированного состояния основания в целом. Однако также очевидно, что в некоторой области основания, которая

находится поблизости от загруженной границы, расхождения с реальной картиной напряженно-деформированного состояния основания будут уже существенными.

Рис. 5.1. Фундаменты различной жесткости:

а – абсолютно гибкий; б – абсолютно жесткий; в – конечной жесткости

Указанная проблема рассматривается в контактных задачах. Под контактной задачей понимают задачу определения НДС на границе контакта между двумя телами и в самих этих телах рядом с границей. В данном случае одним телом является фундамент, другим грунтовое основание.

Знание контактных давлений необходимо при расчете фундамента на прочность и определении НДС в той области основания, которая непосредственно примыкает к фундаменту.

5.2. Уравнение изогнутой оси фундамента

В классической постановке контактной задачи принимаются следующие гипотезы:

фундаментная плита находится в равновесии под действием внешних сил и реакции грунта;

грунт и фундамент деформируются совместно, т.е. отсутствует «отлипание» фундамента от основания;

в рассматриваемых ниже решениях трением по подошве пренебрегаем, т.е. подошвы фундаментов считаем абсолютно гладкими;

для тела фундаментов применима гипотеза плоских сечений. Последняя гипотеза особо важна, поскольку обеспечивает правомерность

применения уравнения изогнутой оси балки при определении внутренних усилий в теле фундамента. Это уравнение является основным при построении классических решений контактной задачи.

Направим ось Ox вдоль оси балки и примем обозначения: прогиб w(x), угол поворота сечения (x), изгибающий момент M(x), перерезывающая сила Q(x), распределенная нагрузка, действующая на балку, q(x). Из курса «Сопротивления материалов» известно, что в балке в сечении с координатой x эти параметры связаны следующими дифференциальными соотношениями, называе-

мыми уравнением изогнутой оси:

где EI постоянная по длине жесткость балки.

Поскольку в дальнейшем решения будем строить преимущественно для условий плоской деформации, то необходимо сделать одно важное уточнение: мы имеем дело не с балкой, а с некоторой загруженной фундаментной полосой (рис. 5.2). Для такой полосы уравнения (5.1) также являются справедливыми с тем отличием, что вместо изгибной жесткости EI балки следует использовать

цилиндрическую жесткость полосы фундамента:

где Ef и f модуль упругости и коэффициент Пуассона материла фундамента, If момент инерции поперечного сечения полосы фундамента.

Рис. 5.2. Схема нагрузок на фундаментную полосу

Для фундамента, на который сверху действует внешнее давление, а снизу реакция грунта, функция q(x) определится как

где f(x) внешняя нагрузка на полосу, как правило, заданная, p(x) реакция по подошве полосы, как правило, искомая.

Поскольку фундамент деформируется совместно с основанием, то его прогиб равен осадке основания: w(x) s(x). Тогда с учетом (5.1) и (5.2):

где wIV d4w/dx4.

В одно дифференциальное уравнение (5.3) входят две неизвестные функции w(x) и p(x). Следовательно, необходимо записать дополнительное уравнение, связывающее вертикальные перемещения w(x) на границе контакта и искомую реакцию p(x).

5.3. О моделях Фусса-Винклера и ТЛДС

Для недостающего уравнения используют одну из двух моделей грунто-

вого основания модель Фусса-Винклера (1801, 1867) и модель линейнодеформируемой среды.

Обе модели подразумевают линейную деформируемость грунта. Отличие

состоит в следующем. В модели Фусса-Винклера предполагается, что деформация происходит только в местах приложения нагрузки (рис. 5.3, а). В модели линейно-деформируемой среды грунт деформируется не только в месте приложения нагрузки, но и на значительном расстоянии от нее (рис. 5.3, б).

Рис. 5.3. Модель Фусса-Винклера (а) и модель линейно-деформируемого основания (б)

Считается, что первый случай лучше описывает поведение более слабых грунтов, например, водонасыщенных глинистых, а второй – более прочных таких, как песчаным и твердым глинистым грунтам. Подробней особенности данных моделей и вытекающие из них следствия рассмотрим далее.

Отметим, что изображение деформированной поверхности на второй схеме (см. рис. 5.3, б) содержит некоторую условность, поскольку под сосредоточенной силой (задача Буссинеска) или погонной нагрузкой (задача Фламана) имеют место бесконечно большие перемещения.

5.4. Основное уравнение модели Фусса-Винклера

Итак, в модели Фусса-Винклера грунт деформируется только в местах приложения нагрузки, причем в каждой точке осадка прямо пропорциональна величине давления. Это допущение называется гипотезой коэффициента постели, которая для условий плоской деформации записывается в виде:

где k коэффициент постели.

Коэффициент постели, как следует из уравнения (5.4), характеризует деформационные свойства основания и численно равен давлению, вызывающему единичную осадку.

Подставляя (5.4) в уравнение изогнутой оси (5.3), имеем

DwIV (x) k w(x) f (x) ,

или

В качестве базового решения можно принять решение однородного уравнения:

wIV (x) 4 4 w( x) 0.

Здесь A1, A2, A3, A4 постоянные интегрирования, получаемые из граничных условий, Y1(x), Y2(x), Y3(x), Y4(x) функции А.Н. Крылова:

5.5. Решение для жесткого фундамента по модели Фусса-Винклера

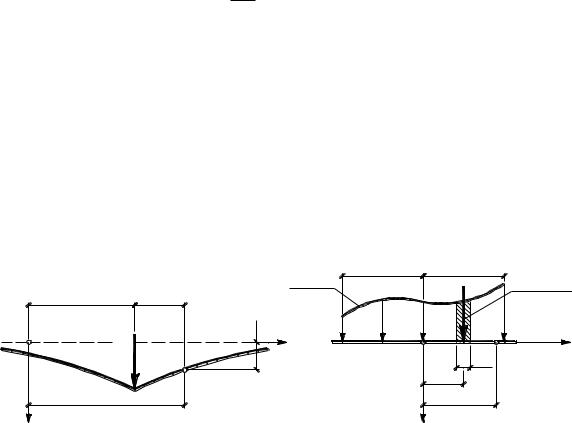
Приведем решение для случая, когда фундамент можно принять абсолютно жестким. На рис. 5.4 приведена расчетная схема такого фундамента шириной 2a, к которому приложена внешняя нагрузка P с эксцентриситетом e.

Рис. 5.4. Абсолютно жесткий фундамент на основании Фусса-Винклера

Линия подошвы абсолютно жесткого фундамента после деформирования остается прямой. Следовательно, ее уравнение можно записать как

w(x) w0 x tg ,

где w0 осадка основания в точке x 0; угол наклона подошвы к горизонту. Согласно (5.4) напряжения по подошве равны

p(x) k w(x) k(w0 x tg ) .

Полученную трапецеидальную эпюру напряжений представим в виде суммы эпюр прямоугольной с равнодействующей 2ak(w0 – a tg ) и треугольной с равнодействующей 2a2k tg , отстоящей от начала координат на a/3. Составим уравнения равенства проекций всех сил на вертикальную ось и равновесия моментов относительно начала координат

2ak(w0 a tg ) 2a2k tg P ; 2a2k tg a / 3 P e .

Решим эти уравнения относительно w0 и tg :

w( x) F ( x ) 1 .

Соответственно, элементарная сила dP p( )d вызовет малое перемеще-

ние:

Если на поверхности задана некоторая распределенная нагрузка (рис. 5.5, б), то на основании (5.6) нетрудно получить перемещение поверхности в точке M от всей нагрузки p(x):

a

w( x) F ( x ) p( )d .

a

Тогда уравнение изогнутой оси подошвы фундамента (5.3) примет вид:

Применяя для подынтегрального выражения функцию осадки поверхности в задаче Фламана (3.6), перепишем (5.7) в виде

Помимо (5.8), искомая функция p(x) должна также удовлетворять уравнениям равновесия сил и моментов, которые для обсуждаемой схемы (см. рис. 5.5, б) имеют вид:

где P и M P e равнодействующая и момент внешних сил относительно центра тяжести плиты.

Существуют несколько подходов к решению основного уравнения (5.8). Так, проф. В.А. Флорин предложил для случая симметричного загружения фундаментной плиты искать решение в виде:

где A и C определяются из граничных условий и уравнений равновесия.

5.7. Решение для жесткого фундамента по модели ТЛДС

Кратко рассмотрим результаты решений контактной задачи для абсолютно жесткого фундамента.

Вертикальные перемещения такого фундамента согласно (3.6) равны:

где угол наклона линии подошвы к оси Ox.

Решение для центрально нагруженного фундамента было получено М.

В.А. Флориным в 1936 г. было дано решение для загружения жесткого фундамента парой сил (рис. 5.6, б):

Суммирование выражений (5.9) и (5.10) дает решение для случая, когда сила P приложена с эксцентриситетом e (рис. 5.6, в):

Все три решения показывают бесконечно большие напряжения под краями фундамента: x a. Понятно, что реальные напряжения не могут быть бесконечно большими, однако этот результат все же имеет определенный практический смысл, поскольку эксперименты показывают, что разрушение оснований жестких фундаментов начинается именно под их краями.

Следует обратить внимание на качественное различие между формами эпюр контактных напряжений, получаемых по моделям Фусса-Виклера и ли- нейно-деформируемой среды. Например, для центрально загруженного абсолютно жесткого фундамента модель Фусса-Винклера дает равномерно распре-

деленную эпюру с ординатой p(x) P/(2a) const, а линейно-деформируемая модель – седлообразную эпюру (см. рис. 5.6, а). Столь сильное отличие в результатах означает, что при решении практических задач выбор модели грунта имеет очень важное значение.

Еще одной особенностью рассмотренных здесь решений является то, что при нагружении парой сил, а также при эксцентриситете e > a/2, на эпюрах появляются отрицательные участки, что согласно принятому правилу знаков означает растяжение. Это ведет к «отлипанию» фундаментов от грунта с последующим перераспределением напряжений по оставшейся площади контакта. В реальном проектировании такой ситуации обычно стараются не допускать. Заметим также, что модель Фусса-Винклера дает «отлипание» жесткого фундамента уже при e > a/3.

Кратко коснемся решений пространственной задачи для абсолютно жестких фундаментов.

Если подошва фундамента имеет форму эллипса, оси которого равны 2a вдоль оси Ox и 2l вдоль оси Oy, то напряжения по подошве составят (e 0):

Для круглого фундамента радиуса R a l напряжения равны:

где r – расстояние от центра подошвы до точки, в которой вычисляются напряжения: r2 x2 y2.