
Лекции / дифф произв
.pdf
Глава 3. Производная и дифференциал функции
§ 1. Определение производной и дифференцирование функции
Пусть |
функция y = f (x) задана |
в точке |
x0 и некоторой ее |
||||
окрестности |
O(x0 ). Рассмотрим переход из точки |
M0 (x0 , y0 ) на |
|||||
кривой в M (x, y) из O(x0 ). |
|
|
|
|
|
||
Величина |
x − x0 обозначается |
символом |
x |
и |
называется |
||
приращением |
аргумента в точке |
x . |
y − y = y |
называется |
|||
|
|
|
0 |
|
0 |
|
|
приращением функции в точке x0 . |
Приращение функции можно |
||||||
выразить по формуле y = f (x0 + x)− f (x0 ). |
|
|
|
||||
Если изменять положение точки M , |
то y = f (x0 |
+ x)− f (x0 ) |
|||||
будет функцией, которая зависит от переменной x .
1
Опр.: Если существует |
|
функции |
y = f (x |
аргумента в точке
конечный предел |
отношения |
приращения |
|
) |
к бесконечно |
малому |
приращению |
x0 |
из области определения функции, то он |
||
называется |
производной |
функции |
|
|
в этой |
|
точке |
и |
||||||||||
обозначается символом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (x0 ): |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
y |
= lim |
f (x + x)− f (x |
) |
= f (x |
|
) |
|
|
|
||||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|||||||
x→0 x |
x→0 |
|
x |
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если найти предел |
lim |
y |
не только в конкретной точке |
x0 , |
||||||||||||||
x |
||||||||||||||||||
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
f (x), где он |
|||||
но и во всех точках из области определения функции y = |
||||||||||||||||||
существует, то получим функцию от |
x . |
Обозначения производной, |
||||||||||||||||
если ее рассматривают как функцию: f |
|
|
|
|
|
|
|
|
dy |
. |
|
|||||||
(x) y |
|
yx f |
|
dx |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Производная |
|
функции |
в |
точке |
показывает, |
|
как быстро |
|||||||||||
изменяется функция в окрестности точки при бесконечно малом изменении аргумента.
Опр.: Операция |
отыскания |
производной |
называется |
|
дифференцированием функции. |
|
|
||
1.1. Найдите производную функции |
f (x)= sin x |
по определению. |
||
|
||||
Аналогично можно получить формулы для отыскания производных основных элементарных функций и составить таблицу производных:
1)xx =1
2)(xn )x = n xn−1; n = const 0
3)(
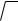 )x = 2 1 xx
)x = 2 1 xx
|
1 |
|
|
|
|
1 |
|
|
|
|||||
4) |
|
|
= − |
|
|
|
|
|
|
|
||||
|
|
x2 |
|
|
||||||||||
|
x |
x |
|
|
|
|
|
|
||||||
5) |
(a x )x = a x ln a; a = const 0, a 1 |
|||||||||||||
6) |
(ex )x = ex |
|
|
|||||||||||
7) |
(log |
|
x) |
= |
1 |
; |
a = const 0, a 1 |
|||||||
a |
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
x ln a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8) |
(ln x) |
|
= |
1 |
|
|
|
|
|
|||||
x |
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
2
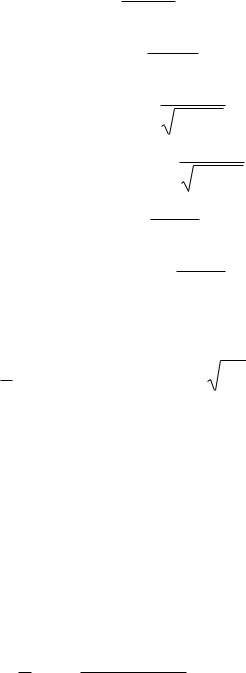
9) |
( |
) |
|
= cos x |
|
|
|
|
|
|
||||
sin x |
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10) |
(cos x) |
x |
= −sin x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11) |
(tgx) |
|
= |
|
1 |
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|||||
|
x |
|
cos |
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
12) |
(ctgx) |
|
= |
− |
|
|
1 |
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
||||||
|
|
x |
|
|
sin |
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
13) |
(arcsin x) |
|
= |
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
|
1 − x |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
14) |
(arccos x) |
|
= − |
|
|
1 |
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|
1− x |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
15) |
(arctgx) |
= |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
x |
|
1+ x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
16) |
(arcctgx) |
|
= − |
|
|
1 |
|
|
|
|||||
|
|
|
|
2 |
|
|||||||||
|
|
|
|
x |
|
|
|
|
1 + x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
1.2. Продифференцируйте функции:
в
v
|
|
|
|
|
3 |
|
x |
|
|
|
|
|
|
|
|
|
5 |
2 |
|||
|
|
|
y = |
|
|
|
z = |
|||
а) |
y = x |
|
; а) |
|
|
; б) u = lg t ; в) |
y . |
|||
|
7 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
Не все функции относятся к основным элементарным, поэтому |
|
случае выполнения простых операций над функциями u = g(x) |
и |
= (x) используют следующие правила дифференцирования: |
|
cx = 0, c = const
(с u)x = с ux
(u + v − w)x = ux + vx − wx (u v)x = ux v + u vx
= ux v − u vx v2
Теор.:Если задана сложная функция |
y = g (x) |
, причем каждая из |
||||
|
|
|||||
функций в композиции имеет производные: |
u = (x) |
в точке |
||||
|
|
|||||
x0 D( ), а y = g(u) в точке 0 |
= ( 0) ( ), |
то сложная |
||||
функция y = g (x) имеет производную в точке |
x0 , которая |
|||||
|
|
|
|
|
|
|
вычисляется по формуле: yx (x0 )= yu (u0 ) ux (x0 ). |
|
|
||||
3

1.3. Найдите производные функций: а) |
y = ( |
x |
|||||||||||||||||||
Производные гиперболических функций |
|
||||||||||||||||||||
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
e |
x |
− e |
−x |
|
|
||
17) |
|
= chx; |
|
|
shx = |
|
|
|
|
|
|||||||||||
shx x |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
−x |
|
|
||
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
e |
+ e |
|
|
||||
18) |
|
= shx; |
|
|
chx = |
|
|
|
|
|
|||||||||||
chx x |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19) |
(thx) |
|
|
|
= |
1 |
|
; |
thx |
= |
shx |
|
|
|
|
||||||
x |
ch |
2 |
x |
chx |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
20) |
(cthx) |
|
= − |
|
1 |
; |
cthx = |
chx |
|
|
|||||||||||
x |
|
|
|
2 |
shx |
|
|
||||||||||||||
|
|
|
|
|
|
|
sh |
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
= chx |
|
|
|
|||
1.4. Докажите, что |
|
shx |
x |
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
+
5)3
; б)
y =
x |
2 |
|
12 + x
+1
.
4

§ 2. Дифференцирование неэлементарных функций
I. Для кусочно заданной функции
f |
(x), |
x X |
|
|
1 |
|
|
|
(x), |
x X |
|
f2 |
|||
f (x)= |
..., |
|
|
|
|
||
|
(x), |
|
|
|
|
x X |
|
fn |
|||
1 2
n
; ;
.
дифференцируют аналитические выражения на отдельных промежутках и уточняют существование производных в точках стыка. Т.к. по определению производная в точке – это предел, то общий предел в точке стыка существует только при совпадении право- и левостороннего пределов в этой точке.
2.1. Продифференцируйте функции:
|
|
x |
2 |
, |
|
|
x −4; |
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
а) |
y = x ; б) f (x)= x + 3, |
− 4 x 0; |
|
||||||||
|
0 x 9; |
|
|||||||||
|
|
x + 2, |
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x 9. |
|
||
|
|
|
|
|
|
|
|
||||
|
x −1, |
|
|
||||||||
II. Для |
параметрически |
|
заданной |
функции |
x = g(t ) |
||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = (t ) |
дифференцирования имеет вид |
|
yx = |
yt |
. |
|
||||||
|
xt |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2.2. Найдите производную |
|
|
|
|
|
|
|
= , |
|||
|
|
|
|
|
|
|
|
||||
yx для функции { = . |
|||||||||||
формула
III. Производные |
для степенно-показательных функций вида |
||
y = (x) g (x ) |
ищут |
методом |
логарифмического |
дифференцирования. Если прологарифмировать такую функцию и применить свойства логарифмов, то после этого дифференцирование упрощается. С другой стороны, производная
|
( |
|
|
сложной функции |
) |
x |
|
ln y |
|
искомую производную
=1 y
yx .
|
y = f (x), остается выразить |
yx , т.к. |
Аналогично можно поступать с
другими функциями, для которых логарифмирование существенно упрощает дифференцирование.
5

2.3. Продифференцируйте функции: а) |
y = |
|||||||
б) |
y = |
|
1− x |
|
(2 − x |
|
7 |
|
3 |
2 |
5 |
) . |
|
||||
|
|
|
|
|
|
|||
Некоторые теоремы о производных
(sin x) |
x |
|
;
Теорема Если функция y = f (x) имеет производную в точке x0 D(f ), то она в этой точке непрерывна.
Обратное не всегда верно, то есть из непрерывности функции в точке еще не следует, что в этой точке существует производная.
Например, в |
x0 |
= 0 |
функция |
y = |
|
x |
|
непрерывна, но производной в ней |
||||||||||||||||
|
|
|||||||||||||||||||||||
нет (2.1.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема Если функции |
|
y = |
f (x) |
|
|
и y = (x) обе бесконечно малые |
||||||||||||||||||
|
или |
|
бесконечно |
большие |
|
|
в точке |
x = a |
или на |
|||||||||||||||
|
бесконечности, то предел отношения функций равен |
|||||||||||||||||||||||
|
пределу отношения их производных в этой точке или на |
|||||||||||||||||||||||
|
бесконечности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
f |
(x) |
= |
|
lim |
f (x) |
, |
|
|
|
(Правило Лопиталя). |
||||||||||||
|
|
(x) |
|
|
|
|
|
|
(x) 0 |
|||||||||||||||
|
x→a( ) |
|
|
x→a( ) (x) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
2 |
−1 |
+ ln x |
|
|
|
|
|
|
|
x |
3 |
−1 |
|
|
|
|||
2.4. Найдите а) |
lim |
|
; б) |
|
|
lim |
|
. |
|
|
||||||||||||||
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
x→1 |
|
|
e |
− e |
|
|
|
|
|
|
|
x→ x |
+1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6
