Вывод: если в т. экстремум, то , , не существует.
Достаточные условия экстремума по первой производной
Теорема (достаточное условие экстремума): Пусть функция дифференцируема в некоторой окрестности точки , может быть за исключением самой точки . Тогда, если при переходе через точку , меняет знак с "+" на "–", то в точке - максимум, а если с "–" на "+" – минимум. Если же не меняет свой знак при переходе через точку , то она не является точкой экстремума.
Исследование на экстремум с помощью производных высших порядков
Теорема:
Пусть
и дифференцируема
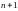 раз в окрестности точки
и
раз в окрестности точки
и
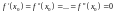 ,
а
,
а
 .
Тогда, если
- четное, то при
.
Тогда, если
- четное, то при
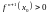 (выпуклость вниз), точка
является точкой минимума, а при
(выпуклость вниз), точка
является точкой минимума, а при
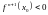 точкой максимума. Если
- нечетное, точка
не является точкой экстремума (т.
является точкой перегиба).
точкой максимума. Если
- нечетное, точка
не является точкой экстремума (т.
является точкой перегиба).
Теорема:
Пусть
имеет в т.
производную и она равна нулю, т.е.
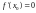 .
Тогда, если
.
Тогда, если
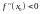 – это точка max,
а если
– это точка max,
а если
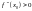 – min.
– min.
Достаточное условие экстремума по второй производной
Пусть для функции y=f(x) выполнены следующие условия:
она непрерывна в окрестности точки x0;
первая производная f′(x)=0 в точке x0;
f′′(x)≠0 в точке x0 .
Тогда в точке x0 достигается экстремум, причем, если f′′(x0)>0, то в точке x=x0 функция y=f(x) имеет минимум; если f′′(x0)<0, то в точке x=x0 функция y=f(x) достигает максимум.
Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
Рассмотрим
произвольный многочлен степени
 :
:
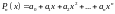 .
.
Где
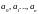 - постоянные числа, коэффициенты
многочлена.
- постоянные числа, коэффициенты
многочлена.
Найдем
последовательные производные и вычислим
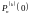 :
:
 ,
,
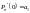
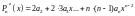 ,
,
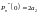
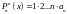
Т.е.
 ,
(
,
( ),
где мы считаем, что
),
где мы считаем, что
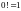 ,
,
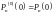 .
.
Тогда получим многочлен Тейлора:
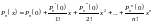
Если
надо представить многочлен вида:
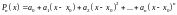 .
Где
- любое фиксированное число. Проделав
аналогичную процедуру получим:
.
Где
- любое фиксированное число. Проделав
аналогичную процедуру получим:
 -
формула Тейлора для многочлена
-
формула Тейлора для многочлена
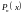 по степеням
по степеням
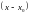 .
.
Любую
функцию можно представить в виде
многочлена:
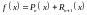 .
Где
- многочлен Тейлора, а
.
Где
- многочлен Тейлора, а
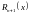 - остаточный член. Т.е.:
- остаточный член. Т.е.:
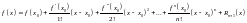 ,
если
,
если
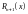 мало, то
мало, то
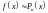 .
.
Остаточный
член в форме Лагранжа:
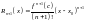 ,
,
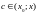 .
.
Замечание: остаточный член мал, как правило, можно пренебречь по сравнению с предыдущим слагаемым.
Рассмотрим
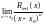 и
и
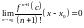 ,
следовательно
,
следовательно
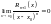 ,
называется б/м более высокого порядка
чем
,
называется б/м более высокого порядка
чем
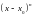 ,
т.е.
,
т.е.
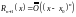 - остаточный член в форме Пеано.
- остаточный член в форме Пеано.
Замечание: если взять минимальное число членов формулы Тейлора, то получатся формулы асимптотического разложения.
,
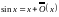
Формула
Тейлора даёт более точное разложение:
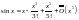
Формула Маклорена
Это формула Тейлора при x0=0
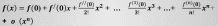
Представление функций ex, sin x, cos x, ln(1+ x), (1+ x)a по формуле Тейлора (Маклорена)

Применение формулы Тейлора для приближенных вычислений
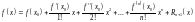 .
.
1)
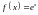 ,
,

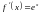 ,
,
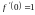
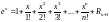 .
.
2)
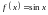 ,
,
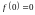
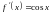 ,
,
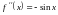 ,
,
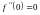
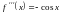 ,
,
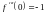
 ,
,
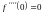
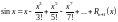 .
.
Направление выпуклости графика функции
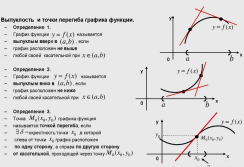
Достаточное условие выпуклости


Точки перегиба
Точка перегиба – это точка, разделяющая интервалы, в которых функция выпукла вниз или вверх.
Необходимое и достаточное условия точки перегиба
Необходимое условие перегиба. Вторая производная f’’(x) дважды дифференцируемой функции в точке перегиба x0 равна нулю.
Достаточное условие перегиба. Если вторая производная f’’(x) при переходе через некоторую точку x0 меняет свой знак, то x0 точка перегиба.
Первообразная
Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого х из этого промежутка F'(x) = f(x).
Пример:
Первообразной для функции f(x)=х на всей числовой оси является F(x)=x2/2, поскольку (x2/2)'=x.
Неопределённый интеграл и его свойства
Неопределенным интегралом от непрерывной на интервале (а; b) функции f(x) называют любую ее первообразную функцию. f(x)dx = F(x)+ c Где С - произвольная постоянная (const).

Замена переменной и интегрирование по частям в неопределённом интеграле


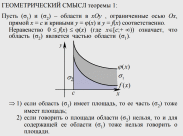
Определённый интеграл и его геометрический смысл
Если функция f(x) непрерывна на промежутке числовой оси, содержащей точки x=а и x=b, то разность значений F(b)-F(a) (где F(x) - первообразная f(x) на данном промежутке называется определенным интегралом от функции f(x) от а до b.
![]()
Свойства определенного интеграла
Определённый интеграл численно равен площади фигуры S, ограниченной осью абсцисс (Ох), прямыми x=а и х=b и графиком функции у=f(x).

Замена переменной и интегрирование по частям в определённом интеграле



Интеграл с переменным верхним пределом


Формула Ньютона-Лейбница


Методы интегрирования рациональных функций
Определение
1. Функция вида 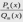 где
где
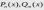 -
многочлены степеней n и m называется
рациональной. Целая рациональная
функция, т.е. многочлен, интегрируется
непосредственно. Интеграл от
дробно-рациональной функции можно найти
путем разложения на слагаемые, которые
стандартным образом преобразуются к
основным табличным интегралам.
-
многочлены степеней n и m называется
рациональной. Целая рациональная
функция, т.е. многочлен, интегрируется
непосредственно. Интеграл от
дробно-рациональной функции можно найти
путем разложения на слагаемые, которые
стандартным образом преобразуются к
основным табличным интегралам.
Определение
2. Дробь  называется
правильной, если степень числителя
n меньше степени знаменателя m.
Дробь, у которой степень числителя
больше или равна степени знаменателя,
называется неправильной.
называется
правильной, если степень числителя
n меньше степени знаменателя m.
Дробь, у которой степень числителя
больше или равна степени знаменателя,
называется неправильной.
Любую неправильную дробь можно представить в виде суммы многочлена и правильной дроби. Это делается посредством деления многочлена на многочлен «столбиком», подобно делению чисел.
Методы интегрирования тригонометрических и иррациональных функций



Приложения определённого интеграла: вычисление в декартовых, полярных и параметрических координатах площади плоской фигуры



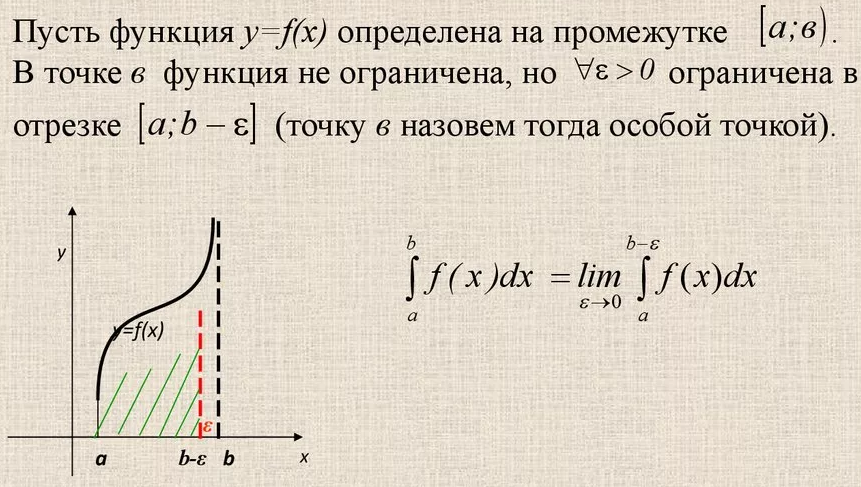
Несобственный интеграл с бесконечными пределами
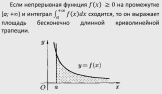

Абсолютная и условная сходимость

Теоремы сравнения



Несобственный интеграл от неограниченных функций (II рода)