
новая папка 1 / 231808
.pdf
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
2 |
2 |
2 |
|
5) Дана матрица A 1 |
7 |
1 |
. Найти обратную матрицу. |
5 |
3 |
3 |
|
|
|
3 |
1 |
1 |
2 |
8 |
|
6) |
Найти ранг матрицы A |
7 |
1 |
2 |
1 |
12 . |
|
|
|
1 |
1 |
3 |
0 |
16 |
|
|
|
11 |
2 |
3 |
3 |
20 |
|
|
|
|
|
2 |
2 |
0 |
1 |
7) |
Найти определитель матрицы A |
2 |
1 |
3 |
0 . |
||
|
|
|
|
0 |
1 |
0 |
2 |
|
|
|
|
9 |
2 |
1 |
0 |
|
1 |
1 |
1 |
|
|
|
|
8) |
Дана матрица A 1 |
3 |
1 |
. Найти обратную матрицу. |
|||
|
5 |
3 |
4 |
|
|
|
|
|
|
|
|
4 |
5 |
|
|
|
|
|
2 |
|
|
||
9) |
Найти определитель |
|
5 |
12 |
11 |
. |
|
|
|
|
3 |
7 |
7 |
|
|
|
|
|
|
4 |
6 |
|
|
|
|
|
1 |
|
|
||
10) Найти определитель |
|
1 |
12 |
19 |
. |
||
|
|
|
1 |
9 |
17 |
|
|
|
|
|
|
|
|
|
|
1.3. Системы линейных уравнений. Матричный способ, правило Крамера. Метод Гаусса
Теоретический материал
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
a11 x1 |
a12 x2 |
a13 x3 |
b;1 |
a21 x1 |
a22 x2 |
a23 x3 |
b2 ; |
a31 x1 |
a32 x2 |
a33 x3 |
b3 . |
Постоянные величины aij (i 1,3; j 1,3) называют коэффициентами системы. Определение: Система чисел x ( x1 ; x2 ; x3 ) называется решением системы уравнений,
если числа x1 , x2 , x3 удовлетворяют этим уравнениям.
Определение: Система называется совместной, если она имеет хотя бы одно решение (x1 ; x2 ; x3 ) , иначе систему называют несовместной.
Определение: Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения.
Введем для системы обозначения:
12

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
a11 |
|
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a21 |
|
a22 |
a23 |
, называемый главным определителем; |
|
|
|||||||||||||
|
a31 |
|
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b1 |
a12 |
|
a13 |
|
|
|
|
|
|
a11 |
b1 |
a13 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x1 |
|
b2 |
a22 |
|
a23 |
; |
|
x2 |
|
a21 |
b2 |
a23 |
; |
|
|
|||||
|
|
b3 |
a32 |
|
a33 |
|
|
|
|
|
|
a31 |
b3 |
a33 |
|
|
|
|||
|
|
a11 |
|
a12 |
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x3 |
|
a21 |
|
a22 |
|
b2 |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
a31 |
|
a32 |
|
b3 |
|
|
|
|
|
|
|
|
|
|
|
|||
Определитель |
|
xi |
получен из главного определителя |
заменой i –го |
столбца |
|||||||||||||||
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
столбцом B |
|
b2 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим три случая: |
|
|
|
|
|
|
|
|||||||||||||
1) |
если |
|
0 , то система имеет единственное решение, определяемое формулами |
|||||||||||||||||
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
||||||
Крамера: x |
i |
|
, |
i 1,3; |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
если |
|
0, но отличен от нуля хотя бы один из частных определителей |
xi , то |
||||||||||||||||
система не имеет решений; |
|
|
|
|
|
|
|
|||||||||||||
3) |
если |
0, |
|
x1 |
0 , |
x2 |
0 , |
x3 0 , то система имеет бесконечное множество |
||||||||||||
решений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если матрица коэффициентов системы невырожденная, то для нахождения решения
применим также и матричный способ. Решением |
матричного уравнения A X B |
||
является матрица–столбец X A 1 B . |
|
|
|
a11 x1 |
a12 x2 |
a13 x3 |
0 |
Определение: Система вида a21 x1 |
a22 x2 |
a23 x3 |
0 |
a31 x1 |
a32 x2 |
a33 x3 |
0 |
называется линейной однородной. |
|
|
|
|||||
Данная система |
всегда |
имеет |
нулевое решение: x1 |
x2 |
x3 |
0 , причем оно |
||
является единственным при |
|
0 . |
В противном случае система имеет бесчисленное |
|||||
множество решений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
x |
2 y |
z 4 |
|
|
|
||
Решить систему |
3x |
5 y |
3z |
1 матричным способом |
и |
с |
помощью формул |
|
|
2x |
7 y |
z |
8 |
|
|
|
|
Крамера |
|
|
|
|
|
|
|
|
Решение
Найдем главный определитель
13

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
3 |
5 |
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
5 |
|
|
21 |
3( |
2 |
7) |
2(6 |
5) |
33. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
|
7 |
|
|
1 |
|
|
|
5 |
|
3 |
|
|
|||||||||||||||||||||||||||||||||
|
2 |
7 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как |
33 |
|
0 , |
то данная система имеет единственное решение. Для матричного |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
способа решения определим алгебраические дополнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5 3 |
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|||||||||||||||||||||||||
A ( 1)1 1 |
|
|
|
|
|
16 ; A ( 1)1 2 |
|
|
9 ; A ( 1)1 3 |
|
|
|
31; |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
11 |
|
|
|
|
|
|
|
7 |
|
|
|
1 |
|
|
|
|
|
12 |
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
2 |
|
|
7 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
||||||||||||||||||||||||
A |
( 1)1 2 |
2 1 |
|
|
|
9; A ( 1)2 2 |
|
|
|
|
3 |
; A ( 1)2 3 |
|
3 ; |
|
|
||||||||||||||||||||||||||||||||||||||||||||
21 |
|
|
|
|
|
|
|
|
7 |
|
|
|
1 |
|
|
|
|
22 |
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
23 |
|
|
|
|
|
|
2 |
7 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
||||||||||||||||||||||||
A ( 1)3 1 |
2 1 |
|
|
11 |
; A ( 1)3 2 |
|
|
|
0 ; |
|
A ( 1)3 3 |
|
|
11. |
|
|
||||||||||||||||||||||||||||||||||||||||||||
31 |
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
32 |
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
9 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
33 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Обратная матрица |
имеет |
|
вид: |
A 1 |
|
|
|
|
|
9 |
|
|
|
3 |
|
0 |
|
|
, |
|
а |
искомое решение |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
33 |
|
|
33 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
3 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
33 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
представляет собой произведение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
16 |
|
|
|
9 |
|
|
|
11 |
|
|
|
64 |
9 |
88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
33 |
|
|
|
|
33 |
|
|
33 |
4 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
X |
9 |
|
|
|
|
3 |
|
|
0 |
|
1 |
|
36 |
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
33 |
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
31 |
|
|
|
3 |
|
|
11 |
|
124 |
3 |
88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
33 |
|
|
|
|
33 |
|
|
33 |
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Составим частные определители:
X
Y
Z
|
4 |
2 |
1 |
|
|
|
|
5 |
3 |
|
|
2 |
|
1 |
|
|
2 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
5 |
3 |
|
4 |
|
|
|
|
|
8 |
|
|
64 |
9 |
88 |
33; |
||||||||||||
|
|
|
7 |
|
|
1 |
|
7 |
|
1 |
5 |
3 |
|
||||||||||||||||
|
8 |
7 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
1 |
|
|
|
1 |
|
3 |
|
|
4 |
1 |
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
1 |
3 |
|
|
|
|
|
3 |
|
2 |
|
|
25 |
36 |
22 |
33; |
|
||||||||||||
|
|
|
8 |
|
1 |
|
8 |
|
1 |
1 |
3 |
|
|
|
|||||||||||||||
2 |
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
5 |
1 |
|
|
2 |
4 |
|
|
|
2 |
4 |
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
5 |
1 |
|
|
|
3 |
|
2 |
|
|
|
47 |
36 |
44 |
33. |
|||||||||||||
|
2 |
7 |
8 |
|
|
|
7 |
|
8 |
|
|
7 |
8 |
|
|
|
5 |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По формулам Крамера имеем: |
x |
x 33 |
1, |
y |
y |
33 |
1, |
z |
z |
33 |
1. |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
33 |
|
33 |
|
33 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
|
|
Задание |
x1 |
2x2 |
3x3 |
5 |
Решить систему 2x1 |
3x2 |
x3 |
7 . |
3x1 |
x2 |
2x3 |
12 |
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
||
|
|
|
2 |
3 |
|
|
5 |
2 |
3 |
|
1 |
5 |
3 |
|
|
||
|
|
|
1 |
|
|
|
|
|
|||||||||
Так как |
|
2 |
3 |
1 |
|
0 , 1 |
7 |
3 |
1 |
0 , 2 |
2 |
7 |
1 |
|
0 , |
||
|
|
|
3 |
1 |
2 |
|
|
12 |
1 |
2 |
|
3 |
12 |
2 |
|
|
|
|
|
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
2 |
3 |
|
7 |
|
0 , то |
система имеет |
бесчисленное |
множество решений. Если |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2x2 3x3 5 |
|
первое |
уравнение прибавим ко второму, |
то получим систему 3x1 |
x2 |
2x |
||||||
|
|
|
|
|
|
|
|
3x1 |
x2 |
2x |
x1 |
2x2 |
3x3 |
5 |
или |
x1 |
2x2 |
5 3x3 |
|
|
|
3x1 |
x2 |
2x3 |
12, |
3x1 |
x2 |
12 |
2x3 . |
|
|
|
|
|
|
||||||||
3
3
12 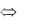
12
|
Пусть x3 – свободная неизвестная, а x1 |
и x2 |
– базисные. Это возможно потому, что |
||||||||||||||||||||||||
|
|
|
2 |
|
7 , т.е. |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Далее, |
|
|
1 |
|
|
|
|
3x3 |
|
2 |
|
29 7x3 , |
2 |
|
|
5 |
3x3 |
|
3 7x3 |
. Следовательно, |
||||||
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||
|
|
|
|
12 2x |
|
|
1 |
|
|
3 |
12 |
2x3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
x1 |
29 |
|
, |
x2 |
3 |
|
|
, |
x3 |
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВОПРОСЫ ЗАДАНИЙ |
|
|
|
|||||
|
Решить систему уравнений матричным способом, с помощью формул Крамера, |
||||||||||||||||||||||||||
Гаусса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
11x |
|
3y |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
|
|
|
2x |
|
5 y |
5z |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
y |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
5 y |
z |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
|
|
|
2x |
|
y |
z |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3x |
|
2 y |
4z |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
15

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
x |
y |
4 |
|
3) |
2x |
3y |
z |
1 |
|
2x |
y |
3z |
11 |
|
2x |
y |
4z |
20 |
4) |
2x |
y |
3z |
3 |
|
3x |
4 y |
5z |
8 |
|
2x |
y |
3z |
7 |
5) |
x |
3y |
2z |
0 |
|
2 y |
z |
2 |
|
|
3x |
4 y |
2z |
8 |
6) |
2x |
y |
3z |
1 |
|
x |
5 y |
z |
0 |
|
x |
2 y |
3z |
6 |
7) |
2x |
3y |
4z |
16 |
|
3x |
2 y |
5z |
12 |
|
3x |
y |
z |
4 |
8) |
x |
5 y |
z |
7 |
|
x |
2 y |
z |
2 |
|
2x |
y |
3z |
3 |
9) |
3x |
4 y |
5z |
8 |
|
2 y |
7z |
17 |
|
|
x |
y |
z 2 |
|
10) |
2x |
y |
6z |
1 |
|
3x |
2 y |
8 |
|
16
ЛИТЕРАТУРА
1.Виленкин, И. В. Высшая математика: линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисление: учебное пособие / И. В. Виленкин, В. М. Гробер. - 6-е изд. - Ростов н/Д.: Феникс, 2011. - 414 с. : ил. - (Высшее образование). - ISBN 978-5-222-18236-9
2.Уейская, Н. Б. Линейная алгебра: учебное пособие / Н. Б. Уейская. - Саратов: ФГОУ ВПО "Саратовский ГАУ", 2011. - 76 с. - ISBN 978-5-7011-0708-1
3.Виленкин, И. В. Высшая математика: линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисление: учебное пособие / И. В. Виленкин, В. М. Гробер. - 6-е изд. - Ростов н/Д.: Феникс, 2011. - 414 с.: ил. - (Высшее образование). - ISBN 978-5-222-18236-9
17
СЛОВАРЬ ТЕРМИНОВ
АЛГЕБРА-наука об изучении объектов произвольной природы АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ – есть минор взятый со знаком плюс, если сумма его индексов чётна и со знаком минус, если сумма его индексов нечётна МАТРИЦА- прямоугольная таблица составленная из элементов любой природы
МИНОР – определитель n-го порядка, составленный из элементов, стоящих н n пересечении любых n строк и n столбцов.
ОПРЕДЕЛИТЕЛЬ – алгебраическая сумма n! Слагаемых составленных из элементов квадратной матрицы РАНГ МАТРИЦЫ – наивысший порядок минора
СИСТЕМА УРАВНЕНИЙ – множество уравнений для которых требуется найти значения неизвестных, удовлетворяющих всем уравнениям системы
18
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ |
4 |
1. ЛИНЕЙНАЯ АЛГЕБРА |
|
1.1. Действия с матрицами |
5 |
ВОПРОСЫ ЗАДАНИЙ |
7 |
1.2. Разложение определителя по строке или |
столбцу. Вычисление |
определителей высших порядков. Обратная матрица |
8 |
ВОПРОСЫ ЗАДАНИЙ |
11 |
1.3. Системы линейных уравнений. |
Матричный способ, правило Крамера. |
Метод Гаусса |
12 |
ВОПРОСЫ ЗАДАНИЙ |
15 |
ЛИТЕРАТУРА |
17 |
ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ |
18 |
19
