Математические основы теории систем

211

15.Существуют ли дробные степени от матриц?

16.Сформулируйте теорему Кэли – Гамильтона.

17.Для чего можно использовать теорему Кэли – Гамильтона?

18.Какие методы используют для вычисления матричных функций?

212

6Векторно-матричные дифференциальные уравнения

6.1Уравнения состояния

Альтернативной дифференциальному уравнению n-го порядка формой описания динамических систем является векторно-матричная форма. Векторноматричная форма по сути является записью дифференциального уравнения n-го порядка в нормальной форме Коши с привлечением дополнительных переменных, называемых переменными состояния.

Определение переменных состояния уже давалось в подпараграфе 1.3.5, но нелишне вспомнить его ещё раз. Переменные состояния системы – это такие переменные, знание значений которых в некоторый начальный момент времени t0 позволяет определить поведение системы в текущий момент времени t > t0 (естественно, если известны входные воздействия системы на интервале (t0 ,t) ). Если ввести обозначения r(t) – входные переменные, y(t) – выходные переменные, x(t) – переменные состояния, то общее математическое описание ди-

намической системы задается уравнениямиЖ

x(t) = δ(x(t0 ),r(τ)),

где δ и λ являются однозначными функциями, а τ – отрезок оси времени от t0 до t .

Уравнения (6.1) называются уравнениями состояния. Часто собственно уравнением состояния называется первое из уравнений (6.1), а второе носит название уравнения выхода.

6.1.1 Каноническая форма фазовой переменной

Если динамическая система описывается или может быть описана обыкновенным линейным дифференциальным уравнением n-го порядка, то переход к нормальной форме Коши дает уравнения состояния такой системы. Переход от дифференциального уравнения к уравнениям состояния может быть произведен различными способами в соответствии с различным определением переменных состояния, важно только, чтобы переменные состояния системы подлежали измерению (контролю).

213

Например, перейти от дифференциального уравнения к уравнениям состояния можно следующим образом. Пусть (для простоты) в дифференциальном уравнении отсутствуют производные входного воздействия. Также, не снижая общности, можно положить коэффициент при старшей производной единице. Тогда дифференциальное уравнение имеет вид

Переменные состояния введем следующим образом: x1 = y,

x2 = xɺ1 = yɺ,

...

xn = xɺn−1 = y(n−1).

Подставив значения y и его производных в уравнение (6.2), найдем: xɺn = −an x1 − an−1x2 − ... − a1xn + r .

Полученные уравнения запишем в нормальной форме Коши, то есть первые производные перенесем в левую часть, а все остальное – в правую. В результате получим систему уравнений:

Уравнения состояния (6.4) с матрицами вида (6.5) носят название канонической формы фазовой переменной (у некоторых авторов можно встретить

214

название стандартной формы). Матрица А вида (6.5) называется матрицей

Фробениуса.

Уравнения (6.4) естественным образом обобщаются на случай многомерной системы, имеющей m входов и р выходов. Тогда в общем виде r и y являются векторами и, кроме того, выход может напрямую зависеть от входа. С учетом этого общий вид уравнений состояния будет такой:

xɺ = A(t)x + B(t)r,

+

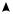
A(t)

Рис. 6.1 – Блок-схема уравнений состояния

Для системы с постоянными параметрами матрицы A(t), B(t), C(t),

D(t) от времени не зависят и могут записываться просто как A, B, C, D. В случае стационарных систем уравнения состояния записываются таким образом:

xɺ = Ax + Br,

(6.7)

y = Cx + Dr.

6.1.2 Каноническая форма

При исследовании систем, описываемых уравнениями состояния, часто является удобным такой выбор переменных состояния, чтобы разноименные компоненты вектора состояния не зависели друг от друга.

Возьмем уравнения состояния (6.7), где, в общем случае, матрица A – произвольная квадратная матрица с различными собственными значениями.

216

6.2 Решение уравнений стационарных систем

6.2.1 Переходная матрица и методы ее вычисления

Однородное уравнение для линейной стационарной системы имеет вид

xɺ = Ax, (6.11) где A – квадратная размерностью n матрица с постоянными коэффициентами, x – вектор-столбец переменных состояния. Аналогично скалярному случаю, общее решение уравнения (6.11) ищется в виде

рование по всем правилам, удостоверимся, что оно (выражение (6.12)) действительно является решением однородного дифференциального уравнения. Под-

t=t0

Матрица Φ(t − t0 ) = eA (t−t0 ) , удовлетворяющая однородному дифференциальному векторно-матричному уравнению (6.11), называется переходной матрицей, или фундаментальной матрицей. Термином «фундаментальная матрица» чаще пользуются математики, связанные с матричными дифференциальными уравнениями, а словосочетание «переходная матрица состояния» встречается в теории управления и теории систем. Прилагательное «переходная» обусловлено тем, что с помощью матрицы Φ(t − t0 ) осуществляется «переход» системы от некоторого начального состояния x(t0 ) к текущему состоянию x(t). Часто для простоты начальный отсчет времени полагают равным нулю t0 = 0 .

Для вычисления переходной матрицы Φ(t) используют несколько методов. Из уже рассмотренных сюда относятся методы, основанные на теореме Кэли – Гамильтона и теореме разложения Сильвестра (см. примеры 5.8 и 5.9).

К другим методам относятся метод разложения в степенной ряд и метод, основанный на преобразовании Лапласа.

Метод разложения в степенной ряд. Согласно уравнению (5.36) переходную матрицу Φ(t) можно представить бесконечным рядом

Вычисление ряда (6.13) – задача трудоемкая, особенно если ряд сходится медленно, а порядок матрицы Φ(t) недостаточно низкий. Степени матрицы Ak могут быть найдены с использованием теоремы Кэли – Гамильтона. После выполнения суммирования необходимо найти в замкнутом виде все элементы матрицы Φ(t). Количество членов при вычислении ряда (6.13) определяется скоростью сходимости: ограничиваются числом N членов ряда, если относительный вклад (N +1)-го слагаемого в уже вычисленную сумму для каждого элемента матрицы Φ(t) становится меньше наперед заданного числа.

Таким образом, в этом методе для вычисления переходной матрицы необходимо найти обратную матрицу [sE − A]−1 и применить к ней обратное преобразование Лапласа.

······················· Пример 6.1 ······················

Найти переходную матрицу для матрицы A из примера 5.8:

Выражение (6.20) представляет собой еще один метод вычисления переходной матрицы (с использованием модальной матрицы).

······················· Пример 6.2 ······················

Найти переходную матрицу с помощью модальной матрицы для матрицы A из примера 6.1:

Присоединенная матрица Adj[λE − A] равна:

каждая из которых даст свой собственный вектор как ненулевой столбец. Составим из этих векторов модальную матрицу M и найдем обратную к ней M−1 :

На основе (6.20) получаем:

·······································································

6.2.2 Общее решение неоднородных уравнений

Уравнения состояния линейной стационарной системы задаются согласно (6.7) в виде

220

Матрица A в этих уравнениях – основная матрица системы, так как ее структура определяет переходную матрицу состояния. От этой матрицы зависит как вынужденная (установившаяся), так и переходная составляющие решения. Матрица B – матрица связи: структура этой матрицы определяет характер связи входных воздействий с переменными состояния. Матрица C – также матрица связи, а именно связи переменных состояния с выходными переменными системы. Наконец, матрица D – опять матрица связи; на этот раз связи входных переменных непосредственно с выходными переменными. Часто для реальных систем D является нулевой матрицей, так что связь входа непосредственно с выходом отсутствует.

Как и в скалярном случае, возможно общее решение уравнений (6.21), (6.22) для x(t) и y(t) получить разными методами. Можно показать, что в результате решение для x(t) будет равно:

Решение для y(t) следует из подстановки уравнения (6.23) в уравнение выхода (6.22):

Выражения (6.23) и (6.24) являются решениями уравнений состояния (6.21), (6.22). Первое слагаемое в уравнении (6.24) представляет собой переходную составляющую решения, обусловленную начальными условиями, тогда как второе слагаемое (по сути, это интеграл свертки) является вынужденной составляющей, зависящей от входного воздействия.

6.3 Решение уравнений нестационарных систем

6.3.1 Переходная нестационарная матрица

Если параметры системы изменяются во времени, то элементы матрицы A не являются постоянными, а являются функциями времени. В этом случае однородное векторно-матричное дифференциальное уравнение имеет вид

(6.25) При решении этого уравнения естественно обратиться к скалярной анало-

гии, то есть к скалярному уравнению