Компьютерная геометрия и графика
..pdf
61
Центр: [m,n] =[3;−1] .
Конечная точка: при x = 3 , y = (−2 ± 32 )
2,
то есть может быть две конечные точки [ 3; 1.8 ] [3; - 3.8 ].
Y 
E1
S
C X
E2
Рисунок 3.1
Параметрическое представление окружности задается следующим образом:
x = r cosθ ;
y = r sinθ ,
или другим способом :
x = |
1−t2 |
y = |
|
2t |
. |
||
|
|
|
|
|
|||
1 |
+t2 |
|
+t2 |
||||
|
1 |
|
|||||
(Здесь t = tg (θ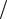
2) ).
При выборе способа задания окружности необходимо учитывать ряд моментов, связанных с вычислительной эффективностью алгоритма визуализации по математическому описанию и качеством воспроизведения.
Во-первых, чтобы распределение точек на кривой при визуализации позволяло хорошо представлять форму кривой.
Y |
|
1 |
|
0 |
X |
1 |
y = 1− x2
62 |
|
Y |
|
1 |
|
0 |
X |
1 |
x = r cosθ
y = r sinθ r =1
Рисунок 3.2
Y |
|
1 |
|
0 |
X |
1 |
=1−t2
x1+t2
y = |
|
2t |
|
+t2 |
|
1 |
||
Из рисунков видно, что использование явного описания при равномерном приращении неизвестной переменной x дает довольно некачественное (неравномерное) распределение точек. Наиболее удачно здесь параметрическое задание через угол θ с равномерным при ращением по этому углу. Однако в вычислительном отношении оно довольно неэффективно, так как требует при вычислении каждой точки считать cos и sin.
Существует способ, позволяющий исключить вычисление тригонометрических функций на каждом шаге. Он основан на применении формул двойного угла:
cos(θ + dθ ) = cosθ cosdθ −sinθ sin dθ ; sin(θ + dθ) = cosθ sin dθ + cos dθ sinθ .
Даже если рассматривать всю окружность, то диапазон изменения угла можно считать фиксированным 0 2π , а приращение dθ – константой.
Тогда xn = r cosθ ; yn = r sinθ ;
иxn+1 = r cos(θ + dθ ) ; yn+1 = r sin (θ + dθ ) ;
63
откуда, с использованием формул двойного угла
xn+1 = xn cos dθ − yn sin dθ ; yn+1 = xn sin dθ + yn cosdθ ,
так как dθ = const , то величины sin dθ и cos dθ необходимо определить только один раз. Таким образом, имеем рекуррентную процедуру построения окружности.
3.3ЭЛЛИПС
Эллипсом называется геометрическое место точек, сумма расстояний которых до двух заданных точек, называемых фокусами, есть величина постоянная (эта постоянная должна быть больше расстояния между фокусами).
Y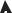 
M
F2 |
F1 X |
Рисунок 3.3
Уравнение эллипса в канонической форме:
(x − m)2 |
+ |
( y − n)2 |
=1; α > β . |
|
α2 |
β2 |
|||
|
|
Приведем его к общему виду (4. 1. 1)
β2 (x − m)2 +α2 ( y − n)2 =α2 β2 ;
β2 x2 +α2 y2 − 2β2mx − 2αny + β2m2 +α2n2 −α2β2 = 0,
то есть
a′ = β2 ;c′ =α2 ;d′ = −2β2m;e′= −2α2n;
f ′ = β2m2 +α2n2 −α2β2 ,
64
то есть уравнение (4. 1. 1) определяет эллипс, если a > 0,c > 0,a ≠ c,b = 0.
Отметим, что это уравнение определяет эллипс в системе координат, в которой оси симметрии эллипса параллельны координатным осям.
Поворот осей координат на угол приводит к изменению коэффициентов:
a= a′cos2 α + c′sin2 α
b= 2(c′− d′)cosα sinα
c= a′sin2 α + c′cos2 α
d= d′cosα + e′sinα
e= e′cosα − d′sinα f = f ′.
Вдальнейшем будем рассматривать систему координат, в которой оси совпадают с осью симметрии кривой, и опустим штрихи у коэффициентов.
Непараметрическое представление эллипса имеет тот же недостаток, что
инепараметрическое представление окружности. При равномерном приращении по оси x точки на кривой не позволяют качественно отобразить ее
форму. Необходимо, чтобы точки вблизи [α,0] располагались чаще, а
вблизи[0,β] – реже.
Y |
X |
Рисунок 3.4 |
Параметрическое представление эллипса задается следующим образом: x =α cosθ ;
y = β sinθ ,
(предполагается, что центр находится в начале координат).
65
Использование формул двойного угла снова позволяет ввести рекуррентную процедуру вычисления координат точек эллипса при равномерном изменении угла θ :
x0 =α y0 = 0
xn+1 = xn cos dθ −α
β yn sin dθ yn+1 = β
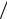αxn sin dθ + yn cos dθ .
Однако и в этом случае точки на кривой располагаются так, что в окрестности с большой крутизной их недостаточно.
Последняя процедура лучше непараметрической лишь с вычислительной точки зрения: здесь не требуется вычислять квадратный корень, как в случае явного представления эллипса.
3.4ПАРАБОЛА
Парабола есть геометрическое место точек, равноотдаленных от данной точки, называемой фокусом, и данной прямой, называемой директриссой
(предполагается, что фокус не лежит на директриссе) т.к. по оси y(±).
( y − n)2 = 2 p(x − n)
Y 
директрисса
M
F X
Рисунок 3.5
66
Уравнение параболы
;(x′− m)2 = 4 p( y′− n);
x′2 − 2mx′− 4 py′+ m2 − 4 pn = 0 ,
то есть a ≠ 0,b = 0,c = 0.
При a =1,d = −2m,e = −4 p, f = m2 − 4 pn ,
( m,n – координаты вершины; p – параметр, определяющий расстояние между
директрисой и фокусом).
Приведенное уравнение представляет параболу, осью симметрии которой является y′. Если x′ и y′ поменять местами, осью симметрии будет x′. Если
p > 0 , то ветви параболы будут направлены в положительную сторону (вверх
или вправо), если p < 0 – в отрицательную сторону (вниз или влево).
Рассмотрим параболу, вершина которой находится в начале координат и
осью симметрии является положительная часть оси |
x . |
В неявной |
|||||
непараметрической форме ее уравнение будет иметь ви |
|
|
|
||||
y2 = 2 px . |
|
|
|
|
|
|
|
Параметрические представления могут быть различны. |
|
|
|
||||
Одно из них: |
|
|
|
|
|
||
|
|
θ |
|
|
|
|
|
x = tg |
|
|
|
|
|
||
|
2 |
0 < θ <π 2 , |
|
|
|
||
|
ptgθ |
|
|
|
|||
|
|
|
|
|
|
||
y = ±2 |
|
|
|
|
|
||
другое: |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x = pθ |
0 <θ < ∞. |
|
|
|
|||
|
|
|
|
||||
y = 2 pθ |
|
|
|
|
|
|
|
Поскольку здесь θ изменяется до ∞ , требуется ввести |
ограничение: |
||||||
значение θmax |
. Например, ограничив ось x , получим θmax = |
|
xmax |
. |
|
||
|
|
|
|||||
|
|
|
|
|
p |
|
|
67
Рекуррентную процедуру вычисления точек параболы в I квадрате с использованием постоянного приращения параметра, можно получить следующим образом:
для θn+1 =θn + dθ
xn+1 = pθn2 − 2 pθndθ + p(dθ2 )
yn+1 = 2 pθn + 2 pdθ ,
то есть x0 = 0 y0 = 0
xn+1 = xn − yndθ + p(dθ )2 yn+1 = yn + 2 pdθ .
Точки кривой в IY квадрате могут быть получены отображением. Такая процедура является и эффективной с вычислительной точки зрения, и позволяет качественно представить форму: вблизи вершины точек больше, чем вдали от нее.
3.5ГИПЕРБОЛА
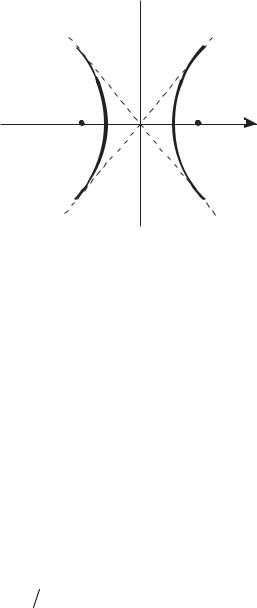
Гиперболой называется геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.
Уравнение:
(x − m)2 |
− |
( y − n)2 |
=1 |
|
α2 |
β2 |
|||
|
|
или
.
Здесь a ≠ 0 и c ≠ 0 ; ac < 0,b = 0.
68
Y
F2 |
F1 X |
Рисунок 3.6
Будем рассматривать гиперболу, центрированную относительно начала координат и с положительной полуосью x в качестве оси симметрии.
Тогда в непараметрическом виде ее уравнение запишется как
x2 |
− |
y2 |
=1. |
|
α2 |
β2 |
|||
|
|
Это уравнение показывает, что вершина ее находится в точке [α,0], а
наклоны асимптот равны ±β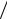
α .
Параметрическое представление задается зависимостями
x = ±α secθ |
0 |
< θ <π 2 . |
|
|
y = ±βtgθ |
||
|
|
|
|
Для получения рекуррентной процедуры снова используем формулы двойного угла:
1 |
|
1 |
|||
sec(θ + dθ ) = |
|
= |
|
||
cos(θ + dθ ) |
cosθ cosdθ −sinθ sin dθ |
||||
tg (θ + dθ) = |
tgθ +tgdθ |
, |
|
|
|
|
|
|
|||
1−tgθtgdθ |
|
|
|
||
таким образом, x0 =α ;
y0 = 0 ;
69
xn+1
xn+1
yn+1
yn+1
= ±asec(θ + dθ) = ± |
|
ab cosθ |
; |
|
|
|
|||
|
bcos dθ −btgθ sinθ |
|||
= |
bxn |
|
; |
|
bcos dθ − yn sin dθ |
|
|
||
=±btg (θ + dθ) = ±btgθ +btgdθ ;
1−tgθtgdθ
=b( yn +btgdθ ).
Другим параметрическим представлением гиперболы является следующее:
x = chθ
y = bshθ .
Из-за того, что в компьютере не обрабатывается отдельно chθ, shθ
(chθ =(e2 + e−2 )
2;shθ = (e2 −e−2 )
2).
Формулы двойного угла для ch и sh : ch(θ + dθ ) = chθ chdθ + shθshdθ ;
sh(θ + dθ) = shθ chdθ + chθshdθ .
Рекуррентная процедура:
xn+1 = xn chdθ + a
b yn shdθ ; yn+1 = b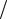
a xn shdθ + yn chdθ .
Эта процедура дает очень хорошее распределение точек на гиперболе.
70
4ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
4.1ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВЕННЫХ КРИВЫХ
Как и плоские кривые, пространственные кривые могут быть представлены непараметрически и параметрически.
Непараметрическое явное задание:
x = x |
|
|
|
|
|
y = f (x) . |
|
|
|
|
|
z = g (x) |
|
|
Непараметрическое неявное задание – кривая на пересечении двух |
||
поверхностей: |
|
|
f (x, y, z) = 0 |
. |
|
g (x, y, z) = 0 |
||
|
||
Параметрическое задание: |
||
x = x(t ) |
|
|
|
< t < t2 . |
|
y = y(t ), t1 |
||
|
|
|
z = z (t ) |
|
|
Многие кривые имеют известное и хорошо изученное аналитическое описание.
Простейший пример – цилиндрическая спираль: |
|
x = α cost |
|
|
= αsin t |
y |
|
|
z = bt |
|
|
где |
|
a – радиус, 2π b – шаг спирали.
Очень часто аналитическое описание неизвестно. В этом случае ставится задача проведения кривой через ряд заданных точек, или проведения кривой, имеющей более сложную зависимость от заданных точек (например, некоторые точки определяют наклон) и т.д.