scherbo-sp2

При обходе в противоположном направлении, т. е. от точки 1 к точке 2, а затем к точкам 3 и 4, на эпюре Sωотс будут знаки, противоположные

показанным на рис. 12.31, а. Напряжения tω для этого случая показаны на рис. 12.31, г, где отсекаемая часть также заштрихована.

Рис. 12.31

Направление касательных напряжений tω в поперечном сечении стержня установим по закону парности. Как видно из рис. 12.31, в, г, на- правление их в точке К остается одинаковым при обоих вариантах обхода.

На рис. 12.31, б показаны эпюра tω и направление их в поперечном сечении стержня.

Числовые значения касательных напряжений tω, как видно из эпюры, по сравнению с числовыми значениями нормальных напряжений в данном случае невелики.

Также малы и касательные напряжения, связанные с поперечным изгибом. Наибольшее из них, возникающее па нейтральной оси ох (см. рис. 12.28, б) сечения, равно

132

М-13. РАСЧЕТ КРИВОГО БРУСА

13.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Общие замечания.

2.Растяжение и сжатие кривого бруса.

3.Чистый изгиб кривого бруса.

4.Определение положения нейтральной оси в кривом брусе при чис- том изгибе.

5.Напряжение при одновременном действии продольной силы и из- гибающего момента.

Цель модуля – изучить методику расчета прочности кривого бруса.

13.1.Общие замечания

Встроительной практике и, в особенности, в машиностроении часто встречаются стержни (брусья) с криволинейной осью. На рис. 13.1 показаны примеры кривых брусьев: крюк подъемного крана, замкнутое кольцо, обод колеса, несущий брус арочного моста – двухшарнирная арка. Все эти брусья отличаются той особенностью, что их ось представляет собой плоскую кри- вую. Брусья с пространственной кривой осью встречаются редко и поэтому здесь не рассматриваются.

Рис. 13.1

В дальнейшем ограничимся рассмотрением таких плоских кривых брусьев, которые имеют симметричные поперечные сечения, а нагрузка лежит в одной плоскости, совпадающей с осью бруса и осью симметрии сечения. При таких условиях все внутренние силы в произвольном сечении кривого бруса приводятся к трем компонентам: нормальной силе N, изги- бающему моменту Мх и поперечной силе Qy.

Определение значений N, Мх и Qy выполняется, как обычно, с помо- щью метода сечений (рис. 13.2). При этом изгибающий момент, так же как и в прямом брусе, подсчитывается относительно оси, проходящей через центр тяжести поперечного сечения.

133

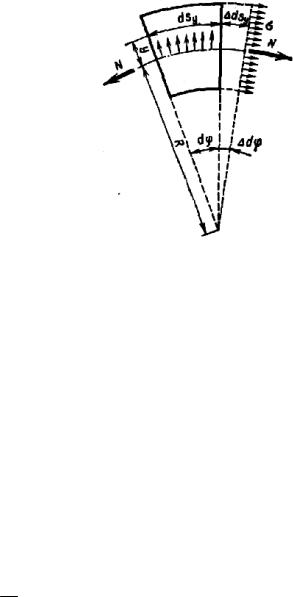
В самом деле, основываясь на гипотезе пло- ских сечений, рассмотрим деформацию элемента бруса, характеризуемую только поворотом сечения на угол dϕ вокруг центра кривизны (рис. 13.5).

Первоначальная длина произвольного во- локна, отстоящего от центра тяжести на рас- стоянии у, равна

dsy = dϕ(R + y),

а удлинение этого волокна равно dsy = dϕ(R + y).

Поэтому относительное удлинение

Эпюра нормальных напряжений показана на рис. 13.5. Равнодейст- вующей соответствующих внутренних сил является продольная сила N, приложенная в центре тяжести сечения:

N = ∫ σdF = σF. (а)

F

Следовательно, рассмотренная деформация соответствует случаю центрального растяжения (сжатия) кривого бруса.

Из формулы (а) получим

σ= N .

F

13.3.Чистый изгиб кривого бруса

Для определения напряжений при чистом изгибе плоского кривого бру- са, так же как для прямого бруса, считаем справедливой гипотезу плоских се- чений. Определяя деформации волокон бруса, пренебрегаем напряжениями в радиальном направлении. Рассматриваем брусья с сечениями, симметричными относительно оси оу, лежащей в плоскости кривизны бруса, и будем счи- тать, что изгибающий момент приложен в той же плоскости.

На рис. 13.6, а, б показан элемент бруса длиной ds с симметричным поперечным сечением. Ось ох направим по нейтральной оси, вокруг кото- рой поворачивается сечение.

135

проходит через центр тяжести, так как в последнем случае должен был бы равняться нулю статический момент ∫ ydF , как это было для прямого бруса.

F

Выразим теперь момент внутренних сил относительно нейтрального слоя через напряжения и приравняем его внешнему моменту, взятому по аб- солютной величине:

Второе слагаемое в полученном выражении согласно равенству (13.2) равно нулю, поэтому

где Sx = Fy0 – статический момент площади поперечного сечения относи- тельно нейтральной оси (у0 – расстояние от центра тяжести сечения до ней- тральной оси).

Подстановка (13.4) в равенство (13.3) дает

Подставляя полученное выражение в формулу напряжений (13.1) и учитывая, что r + y = ρ , т. е. равно расстоянию от центра кривизны до точ- ки, в которой определяется напряжение, окончательно получим

Формула (13.6) существенно отличается от формулы для прямого бру- са прежде всего тем, что в знаменатель входит переменная величина ρ, за- висящая от у.

Эпюра напряжений в сечении кривого бруса изменяется по гипербо-

лическому закону (рис. 13.7). Наибольшие напряжения в сечениях, имею- щих две оси симметрии, возникают в крайнем волокне, обращенном к цен- тру кривизны. Знак напряжения, вычисленного по формуле (13.6), следует определять исходя из физического смысла.

137

Рис. 13.7

Этот интеграл назовем моментом инерции для сечения кривого бруса.

Значок вверху в виде дуги служит отличительным знаком от обычного осевого момента инерции. Легко заметить, что при r → ∞ момент инерции для криво- го бруса в пределе совпадает с обычным осевым моментом инерции.

Таким образом,

Подставляя это выражение в формулу (13.6) и учитывая, что ρ = r + y , получим

Если r → ∞ , то формула (13.8) в пределе совпадает с обычной форму- лой для прямого бруса.

В п. 13.5 дается сравнительная таблица результатов, получаемых по двум формулам: для кривого и прямого брусьев.

13.4.Определение положения нейтральной оси

вкривом брусе при чистом изгибе

Для вычисления напряжений по формуле (13.6), полученной в преды- дущем пункте, необходимо знать, как проходит нейтральная ось. Для этой це- ли надо определить радиус кривизны нейтрального слоя r или расстояние от центра тяжести до нейтральной оси у0 (рис. 13.8). Зависимость между указан-

138

ными величинами y0 = R − r позволяет, зная одну из них, легко определить другую.

Рис. 13.8

При точном решении задачи необходимо исходить из условия (13.2). Для каждого типа поперечного сечения получится свое значение радиуса кривизны нейтрального слоя.

Преобразуем выражение (13.2). Учитывая, что r + y = ρ; y = ρ − r,

получим

139

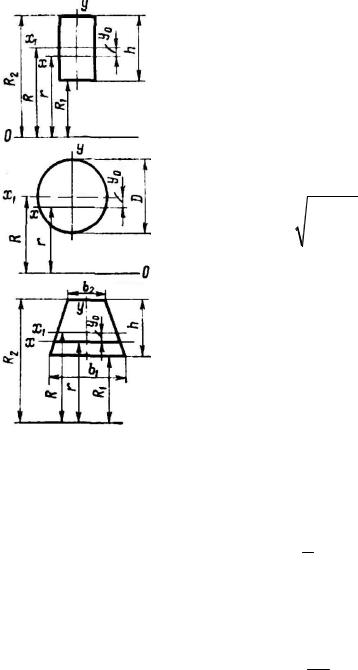
Для некоторых других типов поперечных сечений результаты решения приведены в табл. 13.1

Во многих случаях определение положения нейтральной оси можно произвести приближенно.

Для приближенного решения используем формулу (13.7)

Sx = 1 J x , r

но, с другой стороны (см. (13.4)), имеем

Sx = Fy0.

Приравнивая два полученных выражения, находим

y0 = J x . rF

Чем меньше кривизна бруса, тем больше момент инерции кривого бруса приближается к обычному моменту инерции. Для приближенного решения можно положить

140