2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 8

8.ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ

8.1.Принцип аргумента

Воснове частотных критериев устойчивости лежит известный

втеории функций комплексного переменного принцип аргумента. Пусть дано характеристическое уравнение

Рис. 8.1

Найдем аргумент комплексного числа D( jω):

163

полуплоскости, и числом корней m, лежащих в правой полуплоскости, умноженной на π.

Для устойчивости системы автоматического регулирования, имеющей характеристическое уравнение (8.1), необходимо и достаточно, чтобы число правых корней m было равно нулю, при этом

8.2. Критерий устойчивости Михайлова

Критерий устойчивости А. В. Михайлова, сформулированный им в 1938 году, является наглядной графической интерпретацией принципа аргумента.

Геометрическое место конца характеристического вектора D( jω) при называется годографом вектора D( jω), или годографом Михайлова. Согласно (8.1), уравнение годографа Михайлова

где действительная и мнимая части комплекса D( jω) соответственно будут:

величинами и, таким образом,

165

Учитывая (8.16), уравнение (8.9) можно записать в виде

автоматического регулирования необходимо и достаточно, чтобы при изменении ω от 0 до вектор D( jω) поворачивался на угол n π/2; или, иначе, годограф вектора D( jω), начинаясь при 0 на действительной оси, с ростом ω от 0 до обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n – порядок характеристического уравнения.

На рис. 8.3, а показаны годографы Михайлова для устойчивых систем при различных значениях п. Все они начинаются при 0 со значения an на положительной действительной полуоси. Это означает, что характеристические уравнения приведены к виду, при котором их коэффициенты положительны. Годографы, изображенные на рис. 8.3, а, уходят в бесконечность при и обходят соответствующее число квадрантов в положительном направлении.

а

б

Рис. 8.3

166

На рис. 8.3, б показаны годографы неустойчивых систем. Все они не удовлетворяют условию обхода п квадрантов в положительном направлении.

Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат. Действительно, в этом случае существует значение ω, при котором

наличие в системе незатухающих колебаний, т. е. нахождение ее на границе устойчивости.

Возможен также случай, когда годограф Михайлова идет из начала координат. В этом случае в характеристическом уравнении отсутствует свободный член an 0 и возникает нулевой корень. Выходная величина при этом может принимать произвольные значения. Такую систему называют нейтрально устойчивой.

Пример 8.1. Определить условия устойчивости системы автоматического регулирования (рис. 7.1) с передаточной функцией в разомкнутом состоянии

Cистема будет на границе устойчивости, если годограф D( jω) пройдет через начало координат. Величина kкр может быть определена из уравнений:

167

Решая (8.18) и (8.19), получим

ω20 1/T1T2;

8.3. Критерий устойчивости Найквиста

Для исследования устойчивости усилителей с обратной связью Г. Найквист в 1932 г. предложил критерий устойчивости, основанный на анализе частотных характеристик системы. Согласно этому критерию, для исследования устойчивости замкнутой системы регулирования необходимо знать амплитудно-фазовую частотную характеристику разомкнутой системы, которую можно получить как аналитически, так и экспериментально. Последнее обстоятельство выгодно отличает рассматриваемый критерий устойчивости от ранее изложенных. Заметим также, что критерий Найквиста имеет ясный физический смысл.

Пусть передаточная функция разомкнутой системы регулирования (см. рис. 8.1) W(p) R(p)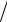Q(p). Образуем функцию

характеристический полином замкнутой системы, знаменатель – характеристический полином, разомкнутой системы. Пусть степень

Рассмотрим три случая состояния разомкнутой системы: устойчивая, неустойчивая и находится на границе устойчивости, причем в последнем случае характеристическое уравнение разомкнутой системы Q(p) 0 имеет нулевой корень кратности ν, т. е.

Q(p) pvQ1(p).

I случай – система в разомкнутом состоянии устойчива. Согласно критерию устойчивости Михайлова изменение

аргумента характеристического полинома разомкнутой системы

168

argQ(jω) n 2.

0 ω

Если потребовать, чтобы система в замкнутом состоянии была устойчива, то должно удовлетворяться равенство

argD( jω) n 2.

0 ω

При этом из (8.21) следует, что

устойчива, если (и только если) изменение аргумента вектора F( jω) при изменении ω от 0 до равно нулю.

На рис. 8.4, а показаны два годографа F( jω) 1 W( jω): 1 соответствует устойчивой системе, так как он не охватывает точку (0, j0); 2 – неустойчивой, так как он охватывает точку (0, j0). Поскольку F( jω) отличается от W( jω) на +1, то условие устойчивости можно получить непосредственно для характеристики

W( jω) (рис. 8.4, б).

Рис. 8.4

Приведем формулировку критерия Найквиста для этого случая. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы W( jω) при изменении ω от 0 до не охватывал точку ( 1, j0).

169

II случай – система в разомкнутом состоянии неустойчива. При рассмотрении многоконтурных систем или одноконтурных

систем, содержащих неустойчивые звенья, разомкнутая система может оказаться неустойчивой.

Пусть система в разомкнутом состоянии неустойчива, при этом характеристическое уравнение разомкнутой системы имеет m корней в правой полуплоскости. Тогда согласно принципу аргумента (8.8), учитывая симметрии характеристик для ω и ω, получим

Отсюда следует формулировка критерия Найквиста. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы W( jω) при изменении ω от 0 до охватывал m/2 раз в положительном направлении точку ( 1, j0), где m – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Очевидно, что формулировка критерия Найквиста для первого случая является частным случаем (m 0) только что приведенной формулировки.

Например, система, W( jω) которой представлена на рис. 8.5, при m 2 будет устойчивой.

Рис. 8.5

170

III случай – система в разомкнутом состоянии находится на границе устойчивости.

Передаточная функция системы в разомкнутом состоянии

где v – число нулевых корней характеристического уравнения системы в разомкнутом состоянии; R(p) и Q1(p) – полиномы от p, причем Q1(p) не имеет нулей в правой полуплоскости и на мнимой оси.

В этом случае нельзя пользоваться приведенными выше формулировками критерия Найквиста, поскольку принцип аргумента, положенный в основу критерия Найквиста, не рассматривает

случай можно свести к случаю устойчивой или неустойчивой системы, что даст возможность применить приведенные формулировки критерия Найквиста

к действительной положительной полуоси. Будем называть эту часть

На рис. 8.6, а показано, как сместился нулевой корень характеристического уравнения разомкнутой системы: она стала устойчивой. При этом интегрирующее звено превратилось в инерционное с постоянной времени и коэффициентом усиления, равными 1/β.

171

Частотная характеристика разомкнутой системы

На рис. 8.6, б показаны частотные годографы W( jω) и W1(jω) соответственно сплошной и штриховой линиями. Они близки друг

кдругу на высоких частотах и отличаются на низких частотах. При

β0 оба годографа совпадают на всех частотах, кроме ω 0:

годограф W1(jω) отличается от W( jω) наличием дуги бесконечного радиуса, проходящей через IV квадрант и приводящей годограф при ω 0 к действительной положительной полуоси (рис. 8.6, в). Эта часть годографа называется «дополнением в бесконечности».

Аналогично строятся измененные частотные годографы при

2,3, .

Рис. 8.6

Для частотных годографов разомкнутых систем, дополненных в бесконечности, можно пользоваться первой формулировкой критерия Найквиста. Для устойчивости замкнутой системы автоматического регулирования, которая в разомкнутом состоянии

172